Основные соотношения динамики конструкций
1.2. Основные соотношения динамики конструкций
1.2.1. Вариационный принцип Гамильтона
Будем рассматривать упругие механические системы, поведение которых описывается линейными дифференциальными уравнениями в частных производных. Так как при решении динамических задач необходимо определить перемещения, напряжения и деформации конструкции как функции пространственных координат и времени, то для формулировки краевых задач динамики необходимо также ввести комплекс начальных и граничных условий.
Для получения основных соотношений динамики воспользуемся вариационным принципом Гамильтона. Согласно этому принципу, из всех кинематически допустимых движений механической системы реально осуществляется такое перемещение точек тела, которое обеспечивает минимум полной энергии. Тогда необходимое условие экстремума функционала примет вид
, (1.18)
где J – гамильтониан, интеграл действия; T – кинетическая энергия; U – потенциальная энергия деформации; П – потенциал внешних сил.
Для упругого тела, занимающего объем V, ограниченного поверхностью S, интеграл действия можно представить в виде
, (1.19)
при этом подынтегральная функция в интеграле действия называется функцией Лагранжа, L - объемная плотность лагранжиана, R - поверхностная плотность лагранжиана, S* - часть поверхности S, на которой действуют внешние нагрузки.
Рекомендуемые материалы
Поведение упругой системы описывается вектор-функцией перемещений U(t,r), объемная и поверхностная плотности лагранжиана, как покажем далее, зависят от функции U и от ее частных производных. Тогда для функционала J можно составить уравнение Остроградского - Эйлера
(1.20)
где 
– повторяющиеся индексы, 
– компоненты вектор-функции U.
Компоненты вектора перемещений связаны с деформациями с помощью геометрических соотношений Коши
. (1.21)
В свою очередь деформации связаны с напряжениями линейным образом по закону Гука для общего случая анизотропии упругих свойств
, (1.22)
где 
– тензор упругих постоянных.
С учетом приведенных соотношений определим выражение для подынтегральной функции в вариационном принципе Гамильтона. Энергию деформирования определим по формуле Клайперона
, (1.23)
подставляя последовательно упругие физические соотношения (1.22) и геометрические выражения (1.21) в уравнение (1.23), получим
. (1.24)
Кинетическая энергия механической системы имеет вид
, (1.25)
где r – плотность материала.
Потенциал внешних сил, представим в виде суммы работ объемных и поверхностных нагрузок
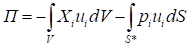
, (1.26)
где 
– компоненты распределенных по объему нагрузок; 
– компоненты действующих на поверхности тела S* нагрузок.
Подставляя полученные для U, T и П соотношения в функционал (1.18) и группируя слагаемые, связанные интегрированием по объему и поверхности деформируемого тела, получим выражение для объемной и поверхностной плотности лагранжианов
, (1.27)
.
Подставляя выражение для объемного лагранжиана в уравнение Остроградского-Эйлера, получим уравнение следующего вида
, (1.28)
известное как динамическое уравнение Ламе. Значение функционала J зависит от значения функции u(t,r) на границе деформируемого тела S*, на этой части границы необходимо сформулировать граничное условие. Данное граничное условие называют естественным, в отличие от оставшейся части границы тела, на которой заданы перемещения точек исследуемой конструкции. В рассматриваемом случае естественное граничное условие примет следующий вид
на S*, (1.29)
где 
– компоненты вектора внешней нормали к поверхности. Тогда, задавая кинематические граничные условия Дирихле на оставшейся части поверхности конструкции
на S**, (1.30)
и дополняя начальными условиями Коши по перемещениям и скоростям в начальный момент времени
при t = 0 , (1.31)
в результате имеем постановку краевой задачи динамики упругого деформируемого тела.
1.2.2. Принцип Даламбера в задачах динамики
Рассмотрим иной способ построения определяющих соотношений динамики, используя принцип Даламбера. Согласно этому принципу динамические уравнения можно получить на основе статической постановки задачи механики деформируемого твердого тела, учитывая инерционные слагаемые в выражениях для уравнений равновесия. Так, статическая краевая задача описывается уравнениями равновесия
, (1.32)
с физическими соотношениями (1.22) и геометрическими уравнениями (1.21) при граничных условиях в напряжениях и перемещениях.
Согласно принципу Даламбера изменения касаются только уравнений равновесия, в которых объемные силы следует представить в виде 
, где первое слагаемое - объемные внешние нагрузки, а второе – силы инерции, определяемые из второго закона Ньютона
. (1.33)
В результате уравнения движения примут вид
. (1.34)
Используя соотношения Гука (1.22) и Коши (1.21) для последовательного исключения из уравнений движения полей напряжений и деформаций, также получим динамическое уравнение Ламе (1.28). Оставляя без изменения граничные условия в перемещениях и исключая напряжения и деформации из граничных условий в напряжениях, получаем граничные условия вида
, (1.35)
совпадающее с естественными граничными условиями для уравнения Остроградского - Эйлера в вариационном подходе. Дополняя полученную систему уравнений начальными условиями
при t = 0 , (1.36)
приходим к точно такой же постановке краевой задачи динамики упругих конструкций, что и для вариационного подхода.
Полученные в разделах 1.2.1 и 1.2.2 постановки краевых задач динамики позволяют исследовать поведение плоских и пространственных тел при действии нестационарных нагрузок. В прикладных расчетах часто приходится проводить анализ стержневых и тонкостенных элементов конструкций, рассмотрим особенности получения определяющих соотношений динамики и для этих практически важных случаев.
1.2.3. Продольные колебания стержней
Стержень – одномерное упругое тело. Пусть ось Х – ось стержня, 
– длина. Стержень совершает продольные колебания, тогда перемещения точек, лежащих в плоскости одного перпендикулярного оси стержня сечения, являются одинаковыми. Получим уравнение движения, используя вариационный принцип Гамильтона
(1.37)
где E – модуль Юнга , F – площадь поперечного сечения.
(1.38)
где q – продольная распределенная нагрузка, N – нагрузка на торцах стержня. Используя уравнение Остроградского - Эйлера получаем уравнение движения
(1.39)
известное в математической физике как волновое уравнение.
Типичные граничные условия для задачи продольных колебаний стержня
1. x жесткая заделка u = 0;
2. x свободный конец 
;
*)
3. N x сила на конце 
;
4. M x масса на конце стержня
;
 |
5. x на конце упругое закрепление
С 
.
1.2.4. Крутильные колебания стержней
Принимаем гипотезу плоских сечений стержня при кручении, пусть 
– угол закручивания. Получим уравнение движения, используя вариационный принцип Гамильтона
, (1.40)
где G – модуль сдвига, 
– полярный момент инерции
; (1.41)
, (1.42)
где m – распределенный крутящий момент; M – крутящий момент на концах стержня. Используя уравнение Остроградского - Эйлера получаем волновое уравнение, описывающее процесс крутильных колебаний стержня
. (1.43)
Типичные граничные условия для задачи крутильных колебаний стержней
1. Жесткая заделка 
;
2. Свободный конец 
;
3. Крутящий момент на конце 
;
4. Инерционный элемент на конце 
;
5. Упругое закрепление на конце 
.
1.2.5. Изгибные колебания стержней
Примем гипотезу плоских сечений, перпендикулярных изогнутой оси стержня. Получим уравнение движения, используя вариационный принцип Гамильтона
, (1.44)
где 
– прогиб стержня, перемещение перпендикулярное оси x, J - осевой момент инерции сечения стержня
; (1.45)
, (1.46)
где q – поперечная распределенная нагрузка по длине стержня, Q – перерезывающее усилие на боковых гранях. Используя уравнение Остроградского-Эйлера, получим уравнение изгибных колебаний стержня
. (1.47)
По сравнению с продольными и крутильными колебаниями увеличивается порядок частных производных по х, следовательно, необходимо большее число граничных условий.
Типичные граничные условия в задаче изгибных колебаний стержней:
1. Жесткая заделка w = 0 ; 
.
2. Шарнирное опирание w = 0 ; 
.
3. Свободный конец ; 
.
4. Сосредоточенная масса 
.
1.2.6. Колебания криволинейных стержней
Введем следующие обозначения: S – криволинейная ось стержня; R(S) – радиус кривизны; 
; u(S) – перемещение вдоль оси S стержня; w(S) – перемещение поперек оси стрежня. Тогда выражения для составляющих полной энергии системы будут иметь вид
(1.48)
Так как динамическое поведение стержня характеризуется функциями U(S) и w(S) получим систему двух уравнений Остроградского-Эйлера
(1.49)
Граничные условия принимаются такие же, как в случае изгиба стержня, но вместо x надо принять S.
1.2.7. Изгибные колебания пластин
Пластина – тело, у которого один из размеров (толщина) много меньше двух других размеров и координатная поверхность которого – плоскость.
Динамическое поведение рассмотрим в рамках технической теории изгиба анизотропных пластин (модель Кирхгофа-Лява). Согласно данной модели:
§ Деформация пластины определяется только прогибом.
§ Нормаль к срединной поверхности после деформирования остается нормальной, прямолинейной и сохраняет свою длину.
§ Срединная поверхность не деформируется.
§ Прогибы пластин малы.
Энергия деформирования определяется следующим образом:
, (1.50)
где W – площадь пластины, Mx, My – изгибающие моменты, Mxy – крутящий момент, cx, cy, cxy, – обобщенные изгибные деформации (кривизны).
Для ортотропной пластины упругие соотношения:
, (1.51)
где Dij – изгибные жесткости:
– однородная анизотропная пластина;
– слоистая пластина.
Исключая момент из выражения энергии деформирования, получим
. (1.52)
Прогибы пластин малы, следовательно, кривизны пропорциональны вторым частным производным прогиба по пространственным координатам
; 
; 
; (1.53)
. (1.54)
Кинетическая энергия (без учета вращений)
. (1.55)
Потенциал внешних усилий (распределенная нагрузка по поверхности q(x,y,t))
. (1.56)
Подставляя полученные выражения в интеграл действия и составляя уравнения Остроградского - Эйлера для функционала, получим
, (1.57)
.
Получили уравнение движения ортотропной пластины при изгибе. Условия на контуре (по два условия).
1. Жесткая заделка.
2. Шарнир.
3. Свободный край: 
– условие Максвелла.
Начальные условия.
1.2.8. Динамическое поведение оболочек
Ограничимся анализом осесимметричных оболочек; вектор перемещений в этом случае описывается двумя компонентами: u – смещение точек срединной поверхности вдоль образующей S; w – смещение точек срединной поверхности вдоль нормали n (рис.1.7).
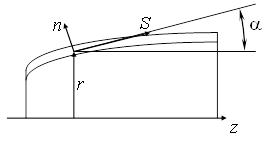
Рис. 1.7. Координатная система осесимметричной оболочки.
В оболочке действуют изгибающие моменты Ms и Mq и усилия в срединной поверхности Ns и Nq.
От действия изгибающих моментов изменяется серединной поверхности, от усилий возникает продольные деформации.
, (1.58)
где l – длина оболочки по меридиану.
Упругие соотношения:
, (1.59)
где для однородной ортотропной оболочки:
(1.60)
при этом 
, если координатная поверхность является срединной поверхностью.
Связь деформаций с перемещениями:
. (1.61)
Подставляя геометрические и физические соотношения в выражения для энергии деформирования, получаем:
. (1.62)
Кинетическая энергия:
. (1.63)
Потенциал высших сил (распределенное давление на поверхность оболочки q(S,t)):
. (1.64)
Подставляя выражения для U, T, П в функционал и сопоставляя для него систему уравнений Остроградского - Эйлера, получаем уравнения движения тонкой анизотропной оболочки (получается система двух дифференциальных уравнений в частных производных относительно функций u(S,t) и w(S,t)).
Граничные и начальные условия формулируются традиционно и приводят к постановке краевой задачи динамики осесимметричной оболочки.
1.2.9. Свободные колебания упругих систем
Анализ полученных ранее уравнений движения упругих систем (плоских и объемных, стержневых и тонкостенных конструкций) показывает, что общая запись уравнений динамики может иметь вид
, (1.65)
где А и С дифференциальные операторы, инерционный и упругий соответственно, 
– поле перемещений, 
– внешняя нестационарная нагрузка.
В случае свободных колебаний упругих систем получается, что внешние нагрузки отсутствуютº 0. В этом случае необходимо исследовать однородное дифференциальное уравнение вида:
. (1.66)
Так как свободные колебания совершаются по гармоническому закону, то общее решение однородного дифференциального уравнения будем искать в виде:
.
(1.67)
Подставляя вид решения (1.67) в уравнение (1.66) получим:
Лекция "Условные графические обозначения" также может быть Вам полезна.
= 0. (1.68)
Значения параметра w2, при которых уравнение (1.68) имеет решение, отличное от j º 0, называют собственными значениями (w, в свою очередь, называют собственными частотами). Функции j, соответствующие собственным значениям w2, называются собственными элементами уравнения (1.68), определяющими собственные формулы колебаний упругой системы. Совокупность собственных частот уравнения (1.68) называют спектром. Спектр собственных частот обычно упорядочивают в порядке возрастания w1 £ w2 £ w3 £ K, причем, w1 – первая (низшая) собственная частота. Собственным формам присваивают номера соответствующих частот, например, j1 - первая форма свободных колебаний механической системы.
Собственные формы ji определяют общее решение уравнения (1.68) (так называемый полный базис) в виде ряда
, (1.69)
где i =1,2K, ui – константы.
*) знак зависит от конца стержня: «+» - левый, «–» - правый.
