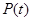Модели надежности ПО
Модели надежности ПО
Классификация моделей надежности ПО
Экспоненциальная модель (модель Шумана)
Вводится ряд допущений и условий, основным из которых является условие существования программы исследователя системы. Остальные допущения и условия не связаны с какими-то специфическими свойствами ПО.
Условия сводятся к следующему:
- Предполагается, что в начальный момент компоновки программных средств системы в них имеются небольшие ошибки (Е – количество ошибок). С этого времени отсчитывается время отладки
![]() , которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени
, которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени ![]() устанавливается
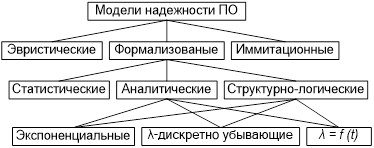
устанавливается ![]() ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду, остающихся в системе после времени
ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду, остающихся в системе после времени ![]() работы равно
работы равно
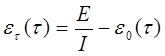
I – общее число машинных команд.
2. Предполагается, что значение функции частоты или интенсивности отказов  пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени
пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени  , то есть
, то есть
Рекомендуемые материалы
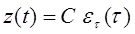
C – коэффициент пропорциональности.
 Тогда, если время работы системы t отсчитывается от момента времени t0, а
Тогда, если время работы системы t отсчитывается от момента времени t0, а  остается фиксированным (
остается фиксированным ( =const), то функция надежности или вероятность безотказной работы на интервале времени от 0 до t есть
=const), то функция надежности или вероятность безотказной работы на интервале времени от 0 до t есть
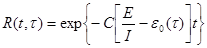
Для нахождения С и Е используются принцип максимального правдоподобия (пропорция).
Модель Джелинского-Моранда
Модель с дискретным убыванием интенсивности отказов. В этой модели предполагается, что интенсивность ошибок описывается кусочно-постоянной функцией, пропорциональной числу не устраненных ошибок. Т.е. предполагается, что интенсивность отказов  постоянна до обнаружения и исправления ошибки, после чего она опять становится постоянной, но с другим, меньшим, значением. При этом предполагается, что между
постоянна до обнаружения и исправления ошибки, после чего она опять становится постоянной, но с другим, меньшим, значением. При этом предполагается, что между  и числом оставшихся в программе ошибок существует прямая зависимость
и числом оставшихся в программе ошибок существует прямая зависимость
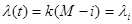
M – неизвестное первоначальное число ошибок
i – число обнаруженных ошибок, зависящих от времени t
k – константа
Частота обнаружения i-ой ошибки  задается соотношением
задается соотношением
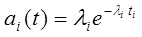
Значения неизвестных параметров k и M может быть оценено на основе последовательности наблюдений интервалов между моментами обнаружения ошибок по методу максимального правдоподобия.
Статистическая модель Миллса
Эту модель можно использовать для сертификации программных средств.
В модели не используются предположения о поведении функции риска  . Эта модель строится на твердом статистическом фундаменте.
. Эта модель строится на твердом статистическом фундаменте.
Сначала программа «засоряется» некоторым количеством известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для ее собственных и внесенных ошибок вероятность обнаружения одинакова и зависит только от их количества. Тестируя программу в течении некоторого времени и отсортировывая собственные и внесенные ошибки можно оценить N – первоначальное число ошибок в программе.
Предположим, что в программу было внесено S ошибок. Пусть при тестировании обнаружено (n+V) ошибок.
n – число собственных ошибок
V – число внесенных ошибок
Тогда оценка для N по методу максимального правдоподобия будет следующей
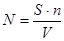
В действительности N можно оценивать после каждой ошибки. Миллс предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и текущие оценки для N.
Вторая часть модели связана с выдвижением и проверкой гипотез о N.
Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь программа тестируется, пока не будут обнаружены все внесенные ошибки. Причем подсчитывается число обнаруженных собственных ошибок n. Уровень значимости С вычисляется по формуле
программа тестируется, пока не будут обнаружены все внесенные ошибки. Причем подсчитывается число обнаруженных собственных ошибок n. Уровень значимости С вычисляется по формуле
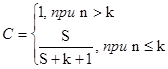
С – мера доверия к модели – вероятность того, что модель будет правильно отклонять ложные предположения.
Формулы для N и C образуют полезную модель ошибок.
Минусы модели
С нельзя предсказать до тех пор, пока не будут обнаружены все внесенные ошибки, это может не произойти до самого конца этапа тестирования.
Модификация формулы для С, если не все ошибки обнаружены:
j – найденные внесенные ошибки, j < S
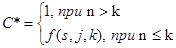
Еще один график, который полезно строить во время тестирования – это текущее значение верхней границы k для некого доверительного уровня.
Модель математически проста и интуитивно привлекательна. Легко представить программу внесения ошибок, которая случайным образом выбирает модуль и вносит логические ошибки, изменяя или убирая операторы. Природа внесения ошибок должна оставаться в тайне, но все их следует регистрировать с целью последующего деления на собственные и несобственные.
Процесс внесения ошибок является самым слабым местом модели, поскольку предполагается, что для собственных и внесенных ошибок вероятность обнаружения одинакова, но неизвестна. Отсюда следует, что внесенные ошибки должны быть типичными, но на сегодня непонятно какими именно они должны быть. Однако по сравнению с проблемами других моделей эта проблема кажется не очень сложной и разрешимой.
Простейшие интуитивные (эвристические) модели
Эти модели особенно эффективны для целей сертификации. Было разработано несколько моделей для оценки числа ошибок. Они основаны на более слабых предположениях, чем сложные модели.
Предполагается начать тестирование двумя независимыми группами. В течение некоторого времени производится параллельное тестирование системы, затем результаты собираются и сравниваются.
N1, N2 – число обнаруженных каждой группой ошибок
N12 – число ошибок, обнаруженных дважды (обеими группами)
N – число ошибок в программе (неизвестное)
Е – эффективность тестирования
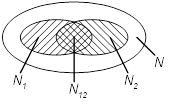

Предполагаем, что возможность обнаружения одинакова. Это серьезное предположение не лишенное смысла. Можно рассматривать каждое подмножество N как аппроксимацию всего пространства.
Например, если первая группа обнаружила 10% ошибок, то она должна было найти примерно 10% всякого случайным образом выбранного подмножества, например подмножества N2. Можно сказать, что
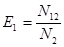
Если выполнить подстановку для N2 получим
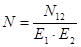
Очевидно, самый простой способ оценки числа ошибок – сравнить оценки, основанные на исторических данных, в частности на среднем числе ошибок, приходящихся на 1 оператор в предыдущих проектах. В литературе есть сведения о частоте ошибок, но они не очень обширны. Имеющиеся данные ориентированы по отраслям и берутся как среднее значение по некоторому количеству операторов (например, 10 ошибок на 1000 операторов).
Пример: данные IBM для OS/360, OS/VS1, OS/VS2:
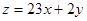
x – многократно исправляемый модуль или число модулей, которые потребовали 10 и более исправлений.
y – число модулей, потребовавших 1 или несколько исправлений.
z – полное число исправлений в модулях.
Из-за неопределенностей во всех рассмотренных модулях пока самый разумный подход – воспользоваться несколькими моделями и объединить их результаты. Например, данные по прежним проектам можно использовать для грубой оценки. Далее можно использовать модель с двумя параллельными группами. Далее – тестирование с искусственным внесением ошибок, определить достоверность С по модели Миллса, а также использовать другие модели.
Объединение результатов нескольких тестов:
- Средняя величина
![]() ,
, ![]()
- Минимальные оценки
- Максимальные оценки
- Интервальные оценки
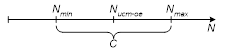
"Гликозиды" - тут тоже много полезного для Вас.
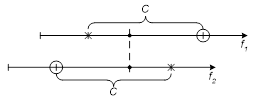
Имитационные модели
Такие модели, которые имитируют процессы появления ошибок, процесс обнаружения ошибок, процесс исправления ошибок с точки зрения надежности ПО.
Часто программу представляют как последовательность узлов, дуг и петель ориентированного графа.
Узлы – точки в которых части программы объединяются или разъединяются.
Дуги – последовательности линейных участков. В них размещаются команды.



 ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду, остающихся в системе после времени
ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду, остающихся в системе после времени  ,
,