Перспективные проекции

Перспективные проекции

Плоская перспективная проекция однозначно определяется положением точки наблюдения и расстояние от нее до плоскости проецирования (d). Положение точки наблюдения может задаваться в виде вектора V, связывающего точку наблюдения и начало трех мерной системы координат, из которой выполняется проецирование. Трехмерная система координат, из которой выполняется проецирование, называется мировой системой координат.

Вектор V может задаваться в одной из двух форм (Рис. 6.2‑1):

1) в полярной системе координат через параметрами:

- r-модуль вектораV;

- Q-угол между координатной осью X и проекцией вектора V на координатную плоскость XY мировой системы координат;

- j-угол между вектором V и осью Z мировой системы координат;

2) в декартовой системе координат через проекции вектора V на координатные оси мировой системы координат:

- V_x – проекция вектора V на ось X;

Рекомендуемые материалы

- V_y – проекция вектора V на ось X;

- V_z – проекция вектора V на ось X.

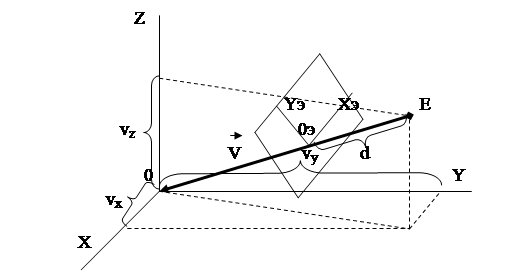Рис. 6.2‑1

Задача проецирования графического объекта, в конечном счете, сводится к определению координат X,Y отдельных точек объекта на плоскости проецирования, которые изначально заданны тремя координатами в мировой системе координат.

Определение координат точки на плоскости проекции

Разобьем общую задачу перспективного проецирования на две задачи преобразования координат:

- преобразование для перехода из мировой системы координат в видовую систему координат

- преобразования для перехода из видовой системы координат в координаты на плоскости проекции.

    Переход в видовую систему координат

Переход в видовую систему координат иллюстрируется ниже приведенным рисунком (Рис. 6.2‑2).

Видовая система координат представляет собой такую трехмерную систему координат с координатными осями X_в, Y_в, Z_в, которая «удобна» для заданной проекции, т.е. из которой наиболее просто осуществляется переход в двумерную систему на плоскости проекции (например, экран). Для данного вида перспективной проекции начало видовой системы  координат должно находиться  в точке E,  ее ось Z_в должна совпадать с вектором проекции V, ее ось X_в должна проецироваться на ось X _э, а ее ось Y _в должна проецироваться на ось Y _э.

ч

Рис. 6.2‑2

Исходя из этого, переход из мировой системы координат в видовую можно выполнить за счет следующей последовательности базовых преобразований:

1) перенос мировой системы координат на вектор V, в результате чего будет получена система координат c началом в точке E и координатными осями X¹, Y¹, Z¹ (реализуется матрицей Т^-1(-V_x, -V_y, -V_z));

2) поворот полученной системы на угол (-(90⁰-q)) относительно ее координатной оси Z¹, в результате чего будет получена система с координатными осями X², Y², Z² (реализуется матрицей R_z^-1(-(90⁰-q)), в которой вектор V находится в координатной полскости Y², Z² ;

3) поворот полученной системы E, X¹, Y¹, Z¹ на угол ((180⁰- j))   относительно ее координатной оси X², в результате чего будет получена система с координатными осями X³, Y³, Z³, начало которой находится в точке E, (реализуется матрицей R_x^-1(180⁰- j)), в которой вектор V располагается на оси Z³; 

4) смена направления координатной оси X³, в результате чего будет получена нужная видовая система координат с координатными осями X_в, Y_в, Z_в (реализуется матрицей R(-x)).

Таким образом, учитывая четыре базовых преобразования координат, для перехода в видовую систему координат необходимо использовать следующее произведение матриц:

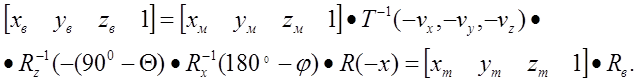
Для задания используемых матриц представим все их элементы через тригонометрические функции  sin j,  cos j,  sin q,  cos q и введем обозначения:

 

cos j= a; sin j = b; cos q = с; sin q  = d;

u_x = -rbc; u_y = -rbd; u_z =-ra.

С этой целью представим перечисленные в выше приведенном выражении матрицы в следующем виде.

Матрица переноса:

T^-1(u_x, u_y, u_z)= T(-u_x, -u_y, -u_z).

Такой представление правомерно, так как обратная матрица переноса на вектор эквивалентна прямой матрицы переноса на этот же вектор в обратной направленности.

C учетом введенных обозначений будем иметь:

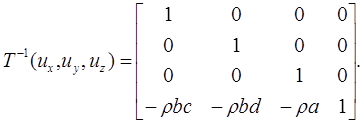
Матрицы поворота относительно оси Z¹:

R_z^-1(-(90⁰-Q))= R_z(90⁰-Q),

и, учитывая, что sin (90⁰-a)=cos a,можно записать:

 

Матрицы поворота относительно координатной оси X²:

R_x^-1((180⁰-j))= R_x (-(180⁰-j)),

и, учитывая, что sin (-(180⁰-j))=- sin j, cos (-(180⁰-j))=- cos j,  имеем:

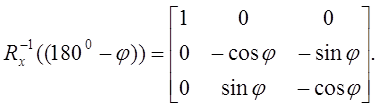
Матрица смены направления координатной оси X² имет вид:

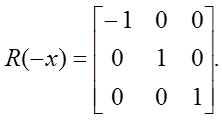
Найдем матрицу видового преобразования R_в:

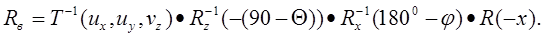
Определим порядок умножения матриц согласно скобок в записи:

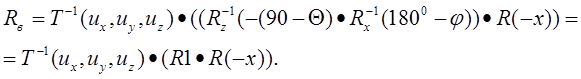
Найдем R1:

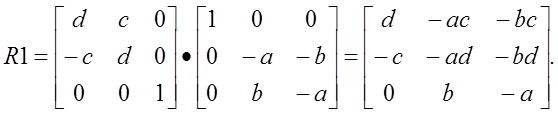
Найдем произведение:

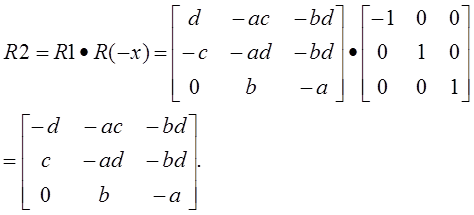
При нахождении матрицы видового преобразования R_в, учтем необходимость расширения матрицы R2 из размерности 3*3 до размерности 4*4:

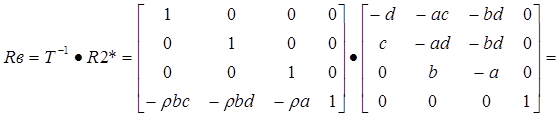
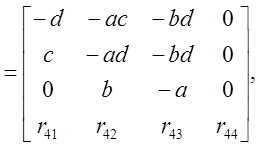
где:

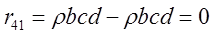
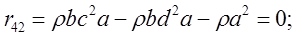
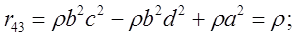
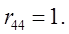
 Таким образом, матрица видового преобразования имеет вид:

                                   (6.2-1)

Переход из видовой системы к координатам на плоскости проекции.

Для выполнения этого этапа используем ниже приведенный рисунок (Рис. 6.2‑3).

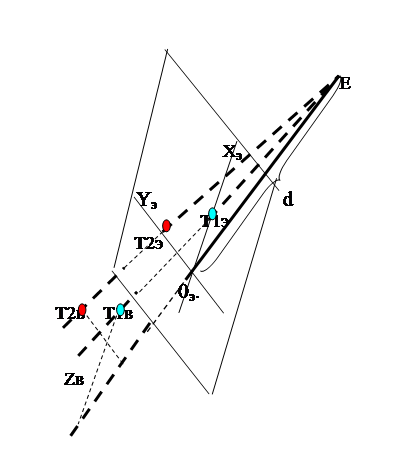Рис. 6.2‑3

На рисунке приняты следующие обозначения:

- Е – начало видовой системы координат с координатными осями X_в, Y_в, Z_в;

- Т1 – точка в видовой системе координат, расположенная на координатной плоскости X_вZ_в;

- Т2– точка в видовой системе координат, расположенная на координатной плоскости Y_вZ_в;

- d - расстояние от начала видовой системы координат до плоскости проекции;

X_э, Y_э  - оси системы координат на плоскости проекции (на экране).

Из приведенного рисунка видно, что:

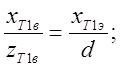
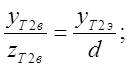
откуда:

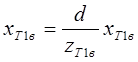
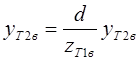
Отсюда вытекает следующая зависимость координат точки на экране от координат  этой точки в видовой системе координат:

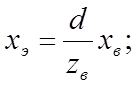
      (6.2-2)

Таким образом, используя матрицу видового преобразования R_в, определяемую выражением (6.2-1), и соотношения согласно выражениям (6.2-2), можно рассчитать координаты заданных точек на плоскости перспективной проекции.

Точки и линии схода

При перспективной  проекции точка схода  прямой АА’ назыавется  та точка на плоскости проекции, к которой стремится проекция точки, «убегающей» в бесконечность по прямой АА’. Для того, чтобы представить геометрический смысл точек схода, рассмотрим  ниже приведенный рисунок (Рис. 6.2‑4).

На рисунке используются следующие обозначения:

 Е -  начало видовой системы координат;

 «пп» -  плоскость проекции (экран) с координатными осями X и Y.

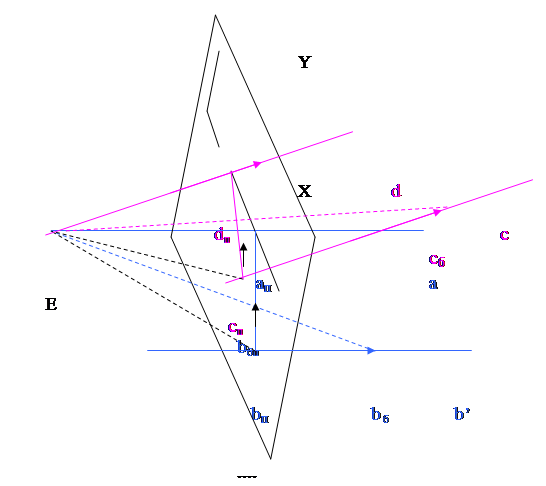Рис. 6.2‑4

Проведем через точку Е прямую Еа’, перпендикулярную плоскости проекции. Эта линия пересекается с плоскостью проекции в точке а_п, которая будет являться точкой проекции всех точек прямой Еа’,  в том числе и точки, убегающей по этой прямой в бесконечность. Следовательно, точка а_п является точкой схода  для линии Еа’.

Возьмем на плоскости проекции некоторую точку b_п и проведем через нее линию b_пb’, параллельную линии Еа’. Проведем через линии Еa’ и b_пb’ плоскость, которая пересечется с плоскостью проекции по линии b_пa_п. Возьмем на линии b_пb‘ точку b_б и устремим ее по прямой в бесконечность.

 По мере перемещения бегущей точки по прямой в бесконечность, ее проекция b_бп будет перемещаться по прямой b_пa_п, стремясь к точке a_п по мере стремления точки b_п в бесконечность. Таким образом, точка a_п будет являться точкой схода для прямой b_пb‘.

Единственным условием для выбора прямой bb’ являлось то, что она параллельна прямой Еa’. Следовательно, для всех прямых, параллельных Еa’,  точкой схода будет являться одна и та же точка a_п.

Проведем в плоскости проекции через точку a_п прямую, параллельную оси X плоскости проекции и возьмем на ней произвольную точку d_п. Проведем прямую через точки E и d_п . Затем  возьмем на плоскости проекции еще одну произвольную точку c_п  и проведем через нее в видовой системе координат прямую c_пc, параллельную прямой  Ed_п.

Через полученные параллельные прямые проведем плоскость, которая пересечет плоскость проекции по прямой d_пс_п. Возьмем на прямой с_пс точку c_б и устремим ее в бесконечность. Как видно из рисунка, по мере перемещения точки c_б. в бесконечность, ее проекция будет перемещаться по прямой c_пd_п., стремясь к точке d_п. Отсюда следует, что точка d_п является точкой схода для прямой с_пс.

 Рассуждая аналогично легко показать, что для всех линий, параллельных плоскости, проходящей через точку E и прямую d_па_п, точки схода будут находиться на линии, проходящей через точки d_па_п.

Из изложенного следует, что прямая d_па_п является линией схода для всех горизонтальных плоскостей. Эта прямая называется линией горизонта.

Из изложенного также можно заключить, что все параллельные линии, независимо от их положения, имеют одну точку схода. Сказанное относится и к вертикальным линиям, которые имеют единую точку схода, называемую точкой зенита.

Рассуждая аналогично, можно показать, что все параллельные  плоскости, имеют единую линию схода.

Понятие точек и линий схода, используется при построении проекций  трехмерных объектов. Рассмотрим это на конкретном примере.

Пусть необходимо построить проекцию параллелепипеда,  с вертикальными боковыми гранями, имеющий верхнюю грань, заданную опорными точками 1, 2,3, 4, и нижнюю, заданную узловыми точками 5, 6, 7, 8 (Рис. 6.2‑5).

Отметим, что из свойства заданного объекта ребра, заданные узловымии точками 1,2; 3,4; 5,6; 7,8, параллельные, а, следовательно, несущие их прямые сходятся в одной точке (точка Тс1). Прямые, несущие боковые ребра 3,7; 4,8; 2,6 и 1,5, так же имеют одну и ту же точку схода ( точка Т3). То же самое можно сказать о  ребрах 1,3; 2,4; 5,7; 6,8 – несущие их прямые параллельны друг другу, а следовательно, имеют единую точку схода (точка Тс2).

Для однозначного построения проекции заданного объекта достаточно на проекции определить  три выше упомянутые точки схода (Т3, Тс1, Тс2), и проекции точек 2,5,6,8 ( Рис. 6.2‑6).

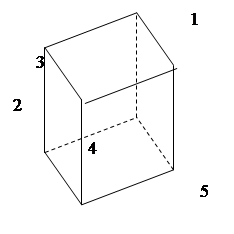Рис. 6.2‑5

Построение проекции можно вести в следующей последовательности.

Через точки 5 и Тс2 проведем прямую линию, несущую ребра 5,7. Ее пересечение с линией, проходящей через точки Тс1 и 8 (прямой линии,

Рис. 6.2‑6

Вам также может быть полезна лекция "Устройство частей и механизмов стрелкового оружия".

несущей ребро 7,8), является точкой  7. Несущие для боковых ребер 3,7; 4,8; 2,6 и 1,5 будут получены, если провести прямые через точку зенита  Т3 и уже имеющиеся четыре  узловые точки нижней грани параллепипеда (линии  Т3,6;  Т3,7;  Т3,8; Т3,5).

Далее через точку 2 и Тс2 проведем прямую, пересечение которой с прямой Т3,8  определяет положение точки 4.

Затем проведем прямые Тс1,2. Точка ее пересечения с прямой Т3,5 будет являться  точка 1. Проведем линии Тс1,4. Точка ее пересечения с прямой T3,7 будет являться точка 3.

Таким образом будет найдены проекции всех узловых точек заданного для проецирования объекта, по которым можно однозначно построить на плоскости проекции весь проецируемый параллелепипед.

Для того, чтобы при проецировании был получен образ объекта, близкий к тому, каким он субъективно воспринимается человеком, необходимо ограничивать угол проецирования  (угол обзора наблюдателем трех мерного объекта из точки наблюдения, т.е. из точки начала видовой системы координат). Как правило, приемлемый результат проецирования получается, когда угол проецирования не превышает 30-40 градусов.

Рассмотренный метод проецирования приемлем лишь для сравнительно простых объектов.