Косоугольные проекции

Косоугольные проекции

Косоугольная проекция определяется углом наклона линии проецирования к плоскости проекции.

Отличие координат X,Y точки в исходной трехмерной системе и одноименных ее координат на плоскости проекции можно проанализировать на примере проекции единичного вектора по оси Z, которая приведена на Рис. 6.3‑1. На рисунке рассматривается случай, когда плоскость проекции совпадает с координатной плоскостью X,Y исходной трех мерной системы, из которой выполняется проецирование.

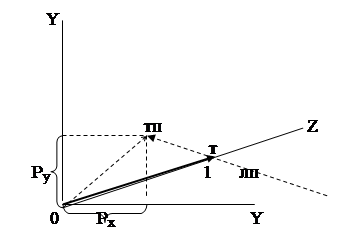Рис. 6.3‑1

Проекцией конца единичного вектора, расположенного на оси Z (точки  «т»), является точка на плоскости проекции, обозначенная как «тп», с координатами P_x и P_y. Эти координаты зависят от наклона линий проецирования, в частности от наклона линии проецирования, проходящей через конец рассматриваемого единичного вектора. С учетом этого, можно записать:

x_тп  = x_т +  Р_x = 0 + Р_x;

y_тп  = y_т +  Р_y = 0 + Р_x.

Рекомендуемые материалы

Величины Р_x и Р_y рассматриваются как  отклонения, соответственно, по координатам X и Y при формировании косоугольной проекции точки.

 Линии проецирования в рассматриваемой проекции параллельные, поэтому можно утверждать, что для всех точек исходной трех мерной системы с координатой по оси Z, равной «1», будет иметь место такие же отклонения  по осям X и Y. Кроме того, очевидно при изменении координаты Z будут пропорционально изменяться отклонения по осям X и Y. Это позволяет записать для любой  точки A(x_A, y_A, z_A) исходной трех мерной системы ее координаты на плоскости проекции как:

x_Aп = x_A + Р_x z _A;

x_Aп = y_A + Р_y z _A.

Матрица, отражающая эту связь координат, имеет вид:

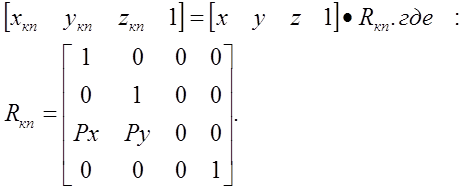
Обратите внимание на лекцию "6 Трансляторы, компиляторы и интерпретаторы".

Для свободной косоугольной проекции имеет место:

Р_x = сos 45⁰;

Р_y = sin 45⁰.

Для кабинетной косоугольной проекии используется уменьшенный масштаб влияния координаты Z на смещение:

Р_x = 0.5 сos 45⁰;

Р_y = 0.5 sin 45⁰.