Устойчивость дискретных систем в моменты квантования

ЛЕКЦИЯ № 14

УСТОЙЧИВОСТЬ ДИСКРЕТНЫХ СИСТЕМ В МОМЕНТЫ КВАНТОВАНИЯ И МЕЖДУ НИМИ.

План лекции:

1. Понятие скрытых колебаний и причины их возникновения.

2. Анализ возможности появления скрытых колебаний.

3. Пример исследования устойчивости ИС.

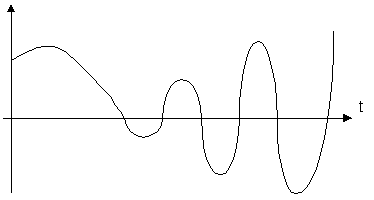
         Ранее, при рассмотрении частотных характеристик ИС, было показано, что z – ПФ  ИС дает информацию о связи ее входа и выхода только в дискретные моменты времени. Поэтому, опираясь на z – преобразование, можно исследовать, соответственно, только так называемую «устойчивость ИС в дискретные моменты времени», которая означает затухание переходного дискретного процесса (рис.4.19).

Рекомендуемые материалы

Рис.4.19.

         Но система, устойчивая в дискретные моменты времени, может оказаться неустойчивой. Этот факт иллюстрирует рис.4.19., на котором показано, что затухающему импульсному переходному процессу , может соответствовать расходящийся переходный процесс  (пунктир). Это – так называемое явление скрытого раскачивания.

         Для получения информации о процессах в моменты времени между моментами квантования предлагается рассматривать ПФ, полученные на основе модифицированного z – преобразования.

         В тактовые моменты времени z – преобразование выходного сигнала имеет вид:

                    .

         Рассмотрим выходной сигнал системы, структурная схема которой приведена на рис.4.20, в смещенные моменты времени.

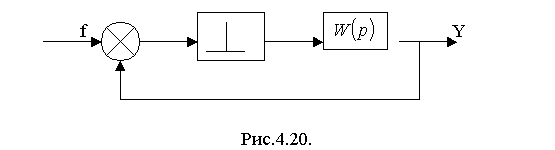
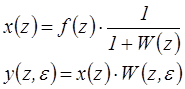
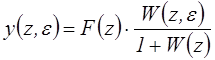
При этом ПФ замкнутой системы для смещенных моментов времени имеет вид:

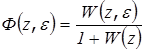
Пусть  , а модифицированная Z –ПФ -        . 

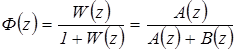
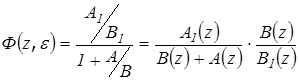
Так как нули многочленов  и  могут не совпадать, то очевидно, что модифицированная Z – ПФ   может иметь полюсы, не входящие в число особых точек ПФ Ф(z). При этом возможны следующие варианты.Если корни полиномов  и  удовлетворяют условиям устойчивости, т. е. имеют модули, меньше единицы, то система устойчива как в тактовые моменты времени, так и между ними.

         Если имеются корни , такие, что , а корни полинома   удовлетворяют условиям устойчивости, то система устойчива в тактовые моменты времени и неустойчива в промежутках между тактами. Это соответствует скрытым колебаниям. При этом на выходе ИИЭ сигнал отсутствует, хотя в системе могут существовать колебания. Отметим, что все способы оценки устойчивости, рассмотренные ранее, определяют устойчивость только в тактовые моменты времени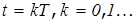

Пример.

Рассмотрим пример исследования устойчивости дискретной системы. Структурная схема системы приведена на рис.4.16

ПФ получена ранее:         .

Построим псевдочастотные ЛАФЧХ системы. С этой целью заменим переменную :

;      и тогда:

;

где ;

   Построим ЛАФЧХ, учитывая, что   и следовательно  (рис.4.17):

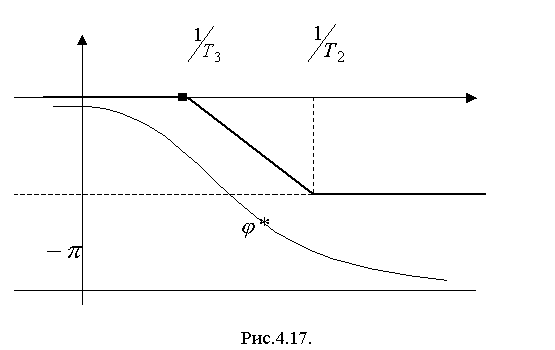
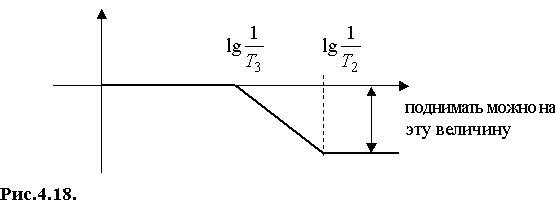
Из построенных характеристик можно заключить, что устойчивость замкнутой системы зависит от величины коэффициента передачи разомкнутой системы (рис.4.18).

Люди также интересуются этой лекцией: 3. Аспекты и структура информационного рынка.

          Условие устойчивости:

;     .
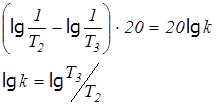