Опорожнение полости постоянного объема

Лекция 24.

Опорожнение полости постоянного объема.

Поделим первое уравнение на второе

.                                                       

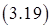
После интегрирования получим уравнение адиабаты Пуассона для идеального газа

,

.

Рекомендуемые материалы

Рассмотрим случай, когда течение из полости в окружающую среду критическое. Перепишем первое уравнение системы (3.18) в виде

.

В полученное выражение подставляем температуру, выраженную из уравнения адиабаты: , получаем

.                                             

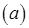
Разделяя переменные и проводя интегрирование в пределах по времени от 0 до  и по давлению – от  до , получим зависимость

.                              

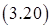
При докритическом режиме течения из полости, т.е. при , также можно представить

.

Но представить аналитической функцией  при докритическом режиме истечения можно лишь для частных случаев, т.е. для определенных значений показателя . Одним из таких частных случаев является случай, когда  (воздух).

 из выражений определяют экспериментально.

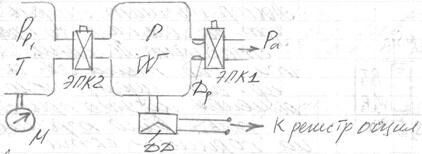
При закрытом ЭПК1 открывается ЭПК2 и полость заполняется из источника до давления . В таком состоянии схема выдерживается некоторое время, чтобы температура газа в полости сравнялась с температурой окружающей среды, затем ЭПК2 закрывают. При открытом ЭПК1 газ истекает в атмосферу, изменяющееся во времени давление в полости регистрируется с помощью датчика давления и осциллографа.

Дросселирующие свойства ЭПК1 должны быть пренебрежимы по сравнению с дросселирующими свойствами испытуемого дросселя .

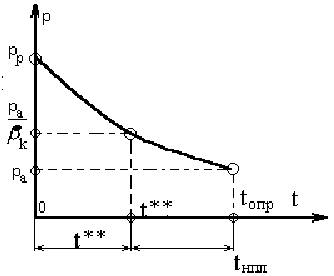
Далее производится расчет

.

Величина  считается осредненной на интервале  и .

Задача.

Построить математическую модель устройства, схема которого представлена на рисунке. Положить, что рабочее тело является идеальным газом, теплообменом можно пренебречь. Сила трения на поршне определяется выражением .

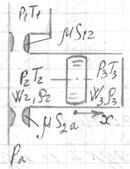
Рассчитать параметры установившегося режима , , ,  при следующих исходных данных

,

,

,

,

,

,

,

,

,

.

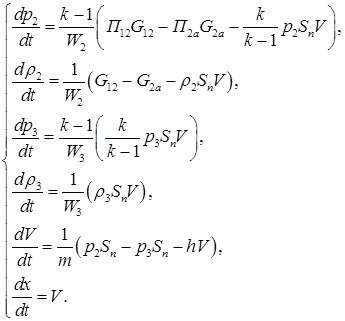
Получим зависимости для установившегося режима, для этого в представленной системе дифференциальных уравнений положим равными нулю все производные по времени

, , , , , .

Из первых двух уравнений следует, что

, .

Делим второе уравнение на третье

.

Откуда следует, что параметры газа в “глухой” полости связаны между собой уравнением адиабаты Пуассона

,

.

Из последнего уравнения получаем

.

Откуда полагаем, что течение является критическим: .

  .

  .

Допуск о том, что  подтвержден, т.к. .

, .

,

откуда

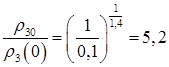
Люди также интересуются этой лекцией: 7.2 Русская культура второй половины ХIХ в.

или

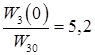
откуда

,

, .

, .