Резонансы в цепях переменного тока
§ 6.5. Резонансы в цепях переменного тока.
1. Резонанс напряжений.
Рассмотрим  - цепь с элементами, включенными последовательно (рис.6.1). Векторная диаграмма тока и напряжений такой цепи приведена на рис.6.14, откуда:
- цепь с элементами, включенными последовательно (рис.6.1). Векторная диаграмма тока и напряжений такой цепи приведена на рис.6.14, откуда:
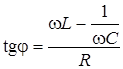
 ; (6.60)
; (6.60)
 . (6.61)
. (6.61)
Из диаграммы рис.6.14 и формулы (6.61) видно, что при  ,
,  ;
;  ;
;  . При таком условии получено максимальное значение тока, что эквивалентно условию:
. При таком условии получено максимальное значение тока, что эквивалентно условию:
 . (6.62)
. (6.62)
При этом  , т.е.
, т.е.  , где
, где  - добротность контура (6.43); при малом затухании
- добротность контура (6.43); при малом затухании  :
:  , т.е. при резонансе
, т.е. при резонансе  и в
и в  раз больше, чем
раз больше, чем  .
.
Рекомендуемые материалы
Исследуем зависимости  . Для этого преобразуем формулы следующим образом. Ток в цепи:
. Для этого преобразуем формулы следующим образом. Ток в цепи:
 (6.63)
(6.63)
Напряжение на элементах цепи:

 ; (6.64)
; (6.64)
 ; (6.65)
; (6.65)
 . (6.66)
. (6.66)
Зависимость угла  - разности фаз между
- разности фаз между  и
и  - от частоты:
- от частоты:
 . (6.67)
. (6.67)
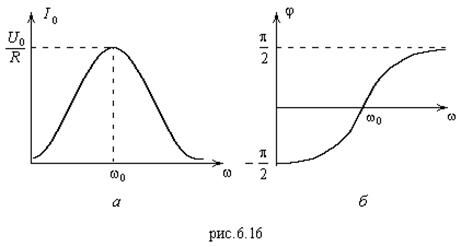
Графические зависимости (6.64) и (6.67) представлены на рис.6.16 (а и б, соответственно).
Достигают ли максимума  и при каких частотах?
и при каких частотах?
Условие  отвечает минимуму знаменателя (6.66).
отвечает минимуму знаменателя (6.66).
 . (6.68)
. (6.68)
Продифференцировав, получаем:  , откуда:
, откуда:
 или:
или:
 . (6.69)
. (6.69)
Максимальное значение  при этом:
при этом:
 . (6.70)
. (6.70)
При совпадении частоты вынужденных колебаний и собственной частоты наблюдается резонанс:  .
.
 |
При
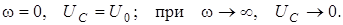
Найдем условие максимума  .
.
 .
.
Упростим:  , откуда:
, откуда:
 . (6.71)
. (6.71)
Значение  при этом:
при этом:
 . (6.72)
. (6.72)
При 
 .
.
При 
Таким образом,  достигают максимума при частотах, не равных
достигают максимума при частотах, не равных  . Оценим, насколько велико это отличие. Так, при
. Оценим, насколько велико это отличие. Так, при  :
:  ;
;  .
.
 Графики частотной зависимости (6.64), (6.65) и (6.66) приведены на рис.6.17. Из графиков видно, что если выходным сигналом является
Графики частотной зависимости (6.64), (6.65) и (6.66) приведены на рис.6.17. Из графиков видно, что если выходным сигналом является  , то контур служит для ослабления высоких частот (высокочастотный фильтр –ВЧ-фильтр). Если же на выходе снимается
, то контур служит для ослабления высоких частот (высокочастотный фильтр –ВЧ-фильтр). Если же на выходе снимается  , то ослабляется низкочастотная часть, и контур служит низкочастотным фильтром (НЧ-фильтром).
, то ослабляется низкочастотная часть, и контур служит низкочастотным фильтром (НЧ-фильтром).
Оценим отличие  по (6.69) и (6.71).
по (6.69) и (6.71).
Для  . Следовательно, при большой добротности, т.е. при малом затухании, можно считать, что максимумы
. Следовательно, при большой добротности, т.е. при малом затухании, можно считать, что максимумы  совпадают по частоте. Величины максимумов
совпадают по частоте. Величины максимумов  в
в  раз больше, чем
раз больше, чем  .
.
2. Резонанс токов.
Резонанс токов происходит в цепи с параллельным включением  и
и  (рис.6.18). Он носит еще название “антирезонанса”, или “параллельного резонанса”.
(рис.6.18). Он носит еще название “антирезонанса”, или “параллельного резонанса”.
 Поскольку изучается цепь с параллельно соединенными элементами, будем оперировать комплексной величиной проводимости
Поскольку изучается цепь с параллельно соединенными элементами, будем оперировать комплексной величиной проводимости  . Емкостная проводимость:
. Емкостная проводимость:
 . (6.75)
. (6.75)
Найдем индуктивную проводимость:
 (6.76)
(6.76)
Суммарная проводимость:
 (6.77)
(6.77)
Условие резонанса имеет следующий вид:
 , (6.78)
, (6.78)
т.е.  . Согласно (6.77):
. Согласно (6.77):  , откуда:
, откуда:
 . (6.79)
. (6.79)
При данном условии  , тогда
, тогда
 (6.80)
(6.80)
где  , по-прежнему, добротность контура.
, по-прежнему, добротность контура.
Ток во внешней цепи  , при этом, имеет минимальное значение (антирезонанс):
, при этом, имеет минимальное значение (антирезонанс):
 . (6.81)
. (6.81)
Найдем значения токов  (см. рис.6.18).
(см. рис.6.18).
 . (6.82)
. (6.82)
Зависимость является линейной по  : ток
: ток  линейно растет с увеличением частоты.
линейно растет с увеличением частоты.
Для случая 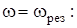
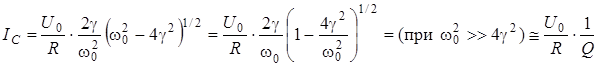
(6.83)
Теперь найдем  .
.
 . (6.84)
. (6.84)
Зависимость индуктивного тока (6.84) является монотонно убывающей функцией частоты.
Для случая 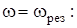
 . (6.85)
. (6.85)
Видно, что при  и
и 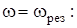
 . (6.86)
. (6.86)
Тогда при 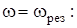
 .
.
Определим частотную зависимость  . Для этого найдем
. Для этого найдем  из (6.77):
из (6.77):
 (6.87)
(6.87)
Таким образом:
 (6.88)
(6.88)
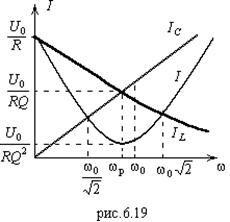
На рис.6.19 изображены зависимости токов (6.82), (6.84) и (6.88) от частоты. При 
 .
.
 .
.
Т.е. при  .
.
Оценим все величины для  :
:
 .
.
 .
.
Из отношения  при
при  можно определить
можно определить  . Из рис.6.19 видно, что вблизи
. Из рис.6.19 видно, что вблизи  происходит ослабление частот (полосовой фильтр).
происходит ослабление частот (полосовой фильтр).
Рассмотрим векторные диаграммы токов и напряжений для цепи рис.6.18.  совпадают по фазе и по величине. Учтем, что:
совпадают по фазе и по величине. Учтем, что:
Рекомендация для Вас - Организационное поведение.
 .
.
 .
.
 Сначала рассмотрим векторную диаграмму для случая
Сначала рассмотрим векторную диаграмму для случая  , так называемого идеального контура, при резонансе (рис.6.20). За исходный примем вектор напряжения
, так называемого идеального контура, при резонансе (рис.6.20). За исходный примем вектор напряжения  на контуре. Так как при резонансе реактивные сопротивления равны
на контуре. Так как при резонансе реактивные сопротивления равны  , одинаковыми будут амплитуды токов
, одинаковыми будут амплитуды токов  и
и  . Ток в индуктивности отстает по фазе от напряжения на контуре
. Ток в индуктивности отстает по фазе от напряжения на контуре  на угол
на угол  =
= , а ток в емкости опережает это напряжение на такой же угол. В результате, векторы токов
, а ток в емкости опережает это напряжение на такой же угол. В результате, векторы токов  и
и  направлены в противоположные стороны. Их сумма равна нулю, что означает отсутствие тока в неразветвленной части цепи.
направлены в противоположные стороны. Их сумма равна нулю, что означает отсутствие тока в неразветвленной части цепи.
 При резонансе в реальном контуре
При резонансе в реальном контуре  расположение векторов на диаграмме несколько иное (рис.6.21). Из-за сопротивления потерь угол
расположение векторов на диаграмме несколько иное (рис.6.21). Из-за сопротивления потерь угол  между векторами
между векторами  и
и  оказывается меньше
оказывается меньше  , поэтому сумма векторов
, поэтому сумма векторов  и
и  дает вектор
дает вектор  , соответствующий некоторому току с амплитудой
, соответствующий некоторому току с амплитудой  в неразветвленной части цепи. Поскольку рассматривается режим резонанса, векторы
в неразветвленной части цепи. Поскольку рассматривается режим резонанса, векторы  и
и  совпадают по направлению, что свидетельствует об активном характере входного сопротивления цепи. Амплитуды токов
совпадают по направлению, что свидетельствует об активном характере входного сопротивления цепи. Амплитуды токов  и в
и в  раз больше амплитуды тока
раз больше амплитуды тока  (см.(6.81), (6.83), (6.86)). Благодаря току
(см.(6.81), (6.83), (6.86)). Благодаря току  в контур от источника поступает энергия, которая рассеивается на активном сопротивлении, поддерживая тем самым постоянство амплитуды колебаний.
в контур от источника поступает энергия, которая рассеивается на активном сопротивлении, поддерживая тем самым постоянство амплитуды колебаний.
 Теперь предположим, что
Теперь предположим, что  . При этом
. При этом  , а
, а  . Векторная диаграмма для этого случая приведена на рис. 6.22.
. Векторная диаграмма для этого случая приведена на рис. 6.22.
Как видно из диаграммы, угол  между векторами
между векторами  и
и  положительный и меньше
положительный и меньше  . Это означает, что ток
. Это означает, что ток  опережает по фазе напряжение на контуре. Длина вектора
опережает по фазе напряжение на контуре. Длина вектора  в рассматриваемом случае больше, чем при резонансе. Это означает, что амплитуда тока в неразветвленной части цепи при
в рассматриваемом случае больше, чем при резонансе. Это означает, что амплитуда тока в неразветвленной части цепи при  (расстройка контура) больше, чем при резонансе. Причина увеличения амплитуды тока заключается в том, что при расстройке контура одновременно с процессом обмена энергиями между электрическим полем конденсатора и магнитным полем катушки происходит обмен энергиями между источником и реактивными элементами контура. Чем больше расстройка, тем большее количество энергии участвует в процессе обмена между источником и элементами контура, и, следовательно, тем больше амплитуда в неразветвленной части цепи. При этом угол сдвига фаз между напряжением
(расстройка контура) больше, чем при резонансе. Причина увеличения амплитуды тока заключается в том, что при расстройке контура одновременно с процессом обмена энергиями между электрическим полем конденсатора и магнитным полем катушки происходит обмен энергиями между источником и реактивными элементами контура. Чем больше расстройка, тем большее количество энергии участвует в процессе обмена между источником и элементами контура, и, следовательно, тем больше амплитуда в неразветвленной части цепи. При этом угол сдвига фаз между напряжением  и током
и током  также увеличивается, стремясь к
также увеличивается, стремясь к  .
.






















