Парадокс Эйнштейна - Подольского - Розена и неравенства Белла

ЛЕКЦИЯ 10. Парадокс Эйнштейна - Подольского - Розена и неравенства Белла.

1. Парадокс ЭПР в варианте Бома. Антисимметричные состояния. Их инвариантность относительно поворота базиса. Аналогия между состояниями частиц со спином 1/2 и поляризационными состояниями света.

2. Неравенства Белла. Классическая модель с двумя дихотомными переменными. Измеряемая Белла. Модель скрытых параметров. Квантовая модель: спонтанное параметрическое рассеяние из двух кристаллов. Роль некоммутирующих операторов.

3. *Парадокс Белла для трех наблюдаемых. Состояния Гринберга - Хорна - Цайлингера. Теорема Белла без неравенств.

В 1935 году А.Эйнштейн, Б.Подольский и Н.Розен предложили мысленный эксперимент, на основании результатов которого они пришли к выводу, что квантовомеханическое описание не является полным и что существуют элементы реальности, которые не учитываются в квантовой механике.

Будем рассматривать т.н. парадокс ЭПР в варианте, предложенном Д.Бомом.

Пусть имеется система двух частиц, так что полный спин системы равен нулю. Например, это может быть электрон-позитронная пара. Другим примером служит двухфотонный распад атома, когда поляризации фотонов ортогональны. И, наконец, при спонтанном параметрическом рассеянии можно так ориентировать кристалл (или пару кристаллов), что излучение в двух пространственных модах будет удовлетворять этому условию.

Совместное состояние пары частиц записывается в виде антисимметричной комбинации спиновых состояний со спином 1/2:

                                                               (10.1)

Рекомендуемые материалы

Здесь  - собственные состояния z-компонент спина i-ой частицы с собственными значениями 1/2. Антисимметричное состояние (10.1) инвариантно относительно вращений. Докажем это утверждение для поляризационного состояния Белла

                                                             (10.2)

где В и С обозначают частицы, а x  y - компоненты линейного поляризационного базиса. Запись  означает двукратное действие оператора рождения на вакуум (в разных поляризационных модах):

                                                                                     (10.3)

Замечание. Формальная аналогия между состояниями частиц со спином 1/2 и поляризационными состояниями света основывается на тождественности коммутационных соотношений операторов проекций момента количества движения j_k частицы со спином J = (1/2)S₀ (операторы Паули) и Стокса, подчиняющимися алгебре Ли (или SU2):

Для операторов Паули:

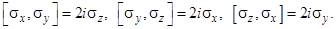
Для операторов Стокса:

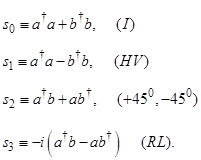
 (конец)

Пусть при произвольном преобразовании поляризационного базиса  его компоненты определяются элементами эрмитовой матрицы:

                                                                   (10.4)

т.е. в матричном виде:

                                                             (10.5)

Тогда компоненты базисов преобразуются по правилам:

                                              (10.6)

Подставив эти выражения в (10.2), получим:

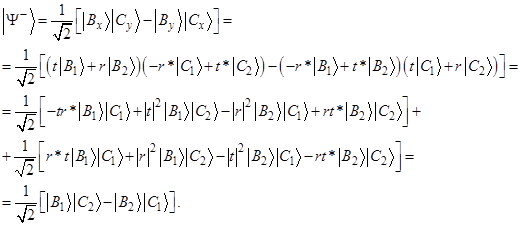
Т.о. синглетное состояние (10.1) инвариантно при произвольных преобразованиях базиса. Другими словами, это состояние имеет один и тот же вид независимо от того, какая ось используется для определения проекции спина. В частности, если выбрано направление “х”, то состояние (10.1) переходит в:

                                                         (10.7)

где  - собственные состояния х-компоненты спина.

Теперь предположим что две частицы разлетелись настолько далеко, что взаимодействием между ними можно пренебречь. Будем производить измерение z-компоненты спина одной частицы (вертикальной поляризации в одном пучке). Это измерение, в соответствии с (10.1), может дать либо значение +1/2 либо -1/2. Если измерение дало результат +1/2, то коррелированная с ней частица должна оказаться в состоянии -1/2. Объясняется это действием проекционного постулата: После проведения измерения над системой, она проецируется на состояние данной наблюдаемой. В данном случае наблюдаемой служит проекция на ось z первой частицы. Поскольку какое-либо влияние между частицами исключено по условию эксперимента, то отсюда делается вывод. что вторая частица имела такое значение проекции спина и до измерения над первой частицей. Т.е. априори существовал элемент физической реальности в виде определенного значения проекции спина второй частицы на ось z.

Теперь предположим, что в эксперименте измеряется х-компонента первой частицы. Согласно инвариантности состояния (10.1) относительно вращений будем рассматривать состояние (10.7), т.е. эквивалентное представление исходного состояния (10.1).

Аналогичные рассуждения приводят к тому, что у второй частицы априори существует определенное значение х-компоненты спина, в зависимости от результата измерения над первой частицей. Наблюдаемой в данном случае является значение х-компоненты спина первой частицы, а полное состояние системы проецируется либо на состояние , либо на состояние .

Поскольку две проекции спина  - несовместные переменные, они соответствуют некоммутирующим операторам, то не существует такого состояния системы, в котором обе переменные имелт бы определенные значения. Отсюда ЭПР сделали вывод о неполноте квантово-механического описания, в которое следует добавить “скрытые” параметры.

Парадокс разрешается в рамках аппарата стандартной квантовой механики. Прежде всего, замети, что поскольку рассматриваемые частицы “1” и “2” взаимодействовали в прошлом, то им нельзя по отдельности приписать волновую функцию. Существует лишь совместная волновая функция . На языке поляризационной оптики это означает, что у обоих пучков степень поляризации равна нулю. Т.о. состояние каждой частицы (в каждом из) пучков является смешанным и его следует описывать с помощью матрицы плотности. Из свойств матрицы плотности следует, что состояние одной из взаимодействующих частиц можно найти, взяв след по “лишним” переменным от матрицы плотности общей системы. Тогда до измерения его состояние есть:

                                                                    (10.8)

Здесь мы учли, что общее состояние описывается волновой функцией, т.е. является чистым. Тогда из (10.8) следует:

                                             (10.9)

Замечание. При выводе (10.9) мы воспользовались тем, что операция Sp оставляет только те компоненты выражения , которые содержат диагональные элементы по первой частице, т.е. вида .

С другой стороны, то же состояние описывается выражением (10.7):

                                       (10.10)

Видно, что оператор плотности второй частицы представляется в виде единичного оператора с точностью до 1/2 (поскольку ).

Что происходит со второй частицей после измерения? Если измерялась z-компонента первой частицы, то состояние второй было с равной вероятностью либо , либо , причем с равной вероятностью. Если же измеряется х-компонента первой частицы, то с равной вероятностью состояние второй частицы оказывается либо , либо . Таким образом оператор плотности до и после измерения имеет один и тот же вид, хотя и описывает результаты разных экспериментов. Значит экспериментально невозможно отличить все эти состояния.

Неравенства Белла

Доказательство неприменимости скрытых параметров для описания некоторых предсказаний квантовых моделей называют теоремой Белла.

Ниже будут рассмотрены случаи двух и трех наблюдателей и дихотомной (или телеграфный сигнал, т.е. сигнал, принимающий два значения) наблюдаемой. Однако если число наблюдателей N растет, то отношение квантового и классического пределов для некоторой наблюдаемой величины S_N растет как 2^(N-1)/2 (Д.Клышко, Д.Мермин)

Неравенство Белла для двух наблюдателей.

Рассмотрим некоторый случайный процесс, который можно характеризовать четырьмя переменными А, А¢, В, В¢. Каждая дискретная случайная величина может принимать два значения, например: А¢ ® а¢ = ± 1, и т.д. (В квантовой теории такой параметризации отвечают операторы некой физической величины и принимаемые собственные значения). Иногда мы будем писать А¢= ± 1 и т.д.

Для наглядности будем полагать, что имеется передатчик, который посылает сообщения двум наблюдателям А и В. У каждого наблюдателя имеется по одной ручке, с помощью которой он может менять свою наблюдаемую: А ® А¢, В ® В¢. В общем случае число положений ручки - произвольно, т.е. наблюдаемые А и В зависят от параметров А(a), В(b). Например, сообщение состоит в команде зажечь лампу красного (-) или зеленого (+) цвета. Одна передача может содержать четыре исхода:  Передачи повторяются многократно, а исход каждой из них случаен. Т.е. независимо от выбора наблюдаемой А или А¢, В или В¢ у каждого наблюдателя загорается красная или зеленая лампа. Эксперимент состоит в выяснении корреляции цвета ламп у разных наблюдателей. Опишем этот процесс математически.

Предположим, что существует положительно определенная нормированная функция совместного распределения вероятностей этих четырех величин:

,                                                                           (10.11)

удовлетворяющая условию нормировки:

.                                                                             (10.12)

Для функций распределения можно вычислять маргинальные вероятности по правилам:

.                                        (10.13)

Введем величину S - т.н. наблюдаемая Белла, которая выражается через моменты наблюдаемых величин:

.                                                     (10.14)

Докажем неравенство Белла (часто его называют неравенством Белла типа Гринберга -Хорна - Шимони - Хольта):

                                                                                                        (10.15)

Функция распределения вероятностей (10.11) состоит из 2⁴ = 16 совместных вероятностей вида:

                                 (10.16)

и т.д. Выразим через эти вероятности средние величины или вторые моменты, входящие в неравенство (10.15) (см. также лекцию 8):

                                       (10.17)

Напомним, что этот момент показывает превышение доли коррелированных сигналов (--) или (++) над некоррелированными (+-) или (-+).

В другом виде (10.17) выглядит так:

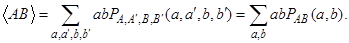
В это выражение входят маргинальные вероятности, которые можно выразить через совместную функцию распределения (10.11). Например,

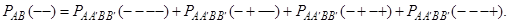
Записывая таким образом все входящие в (10.14) моменты, получаем

                                    (10.18)

В правой части (10.18) стоит знакопеременная сумма. Если бы все знаки были “+”, то мы получили бы условие нормировки (10.12). Но половина слагаемых входит со знаками “-“, и, следовательно, в силу неотрицательности распределения вероятностей (10.11), получаем, что сумма в (10.18) распределена в интервале [-1, +1]. Неравенство (10.15) доказано.

Еще более простой способ доказательства основан на следующем подходе.

Выразим среднее значение случайной величины S, определенной в (10.14), через элементарные вероятности:

                                     (10.19)

Здесь .

Покажем, что эта функция содержит четыре различных множителя и поэтому принимает лишь два значения: ±1. Действительно, сгруппируем слагаемые следующим образом:  Поэтому, если , например, b = b¢, то если же b = - b¢, то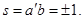

Модуль суммы не превышает суммы модулей, поэтому из (10.19) и условий

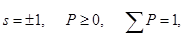
получаем искомое неравенство Белла (10.15):

                                                                  

Таким образом исходя из классического распределения вероятности четырех наблюдаемых величин мы пришли к некоторому соотношению, которому должны удовлетворять моменты (или корреляции) этих величин. Оказывается, что при квантовом описании рассмотренного эксперимента неравенство (10.15) может нарушаться). Происходит это потому, что в классическом случае мы пользуемся понятием совместных вероятностей событий, а в квантовом - с помощью специфической волновой функции, учитывающей возможность парных корреляций. Именно такие корреляции и рассматривались в парадоксе ЭПР.

Почему же этот элементарный вывод теряет силу при квантовом описании? Как только мы ввели совместные вероятности (10.11), мы неявно сделали предположение об априорном существовании и возможности одновременного измерения (в одном испытании) всех четырех величин А, А¢, В, В¢. В квантовых моделях такое предположение не всегда допустимо, когда, например, состояние, записанное на одном фотоне, не может клонироваться или разветвляться по двум каналам. Т.о. два регистрирующих устройства никогда не измеряют такое состояние - фотон не может быть зарегистрирован двумя детекторами. Если говорить о ферми-частицах с полуцелым спином (как при описании парадокса ЭПР в варианте Бома), то наблюдаемым А и А¢ соответствуют разные проекции спина.s_z s_x. Следовательно А и А¢ нельзя измерить в одном испытании.

С формальной точки зрения невозможность одновременного измерения каких-либо наблюдаемых величин в квантовой теории связана с некоммутативностью соответствующих операторов. В нашем случае это  и .Поскольку они не коммутируют, то им нельзя априори приписывать собственные значения +1 или -1. Также не имеют смысла и элементарные вероятности P(a, a¢, b, b¢ ).

            Можно ли избавиться от неравенства , оставаясь в рамках классических представлений об априорных вероятностях? У нас остается лишь две альтернативы.

1. Отказаться от условия неотрицательности вероятностей P ³ 0;

2. Избавиться от равенства s = ±1. Это равенство нарушается если предположить существование каких-то взаимодействий между измерительными приборами. Другими словами выбор наблюдаемой у первого наблюдателя (А или А¢) “нелокально” влияет на показания прибора другого наблюдателя и наоборот. Тогда во всех использованных формулах учесть эту зависимость в виде а(a, b), b(a, b) и т.д.

Тогда s будет зависеть не от четырех, а от восьми множителей:

                     (10.20)

Тогда s может принимать значения 0, ± 1, ± 2. Следовательно в выражении для среднего значения (10.19) должны фигурировать другие элементарные вероятности, которые определяют статистику всех восьми множителей.

Однако теперь все четыре слагаемых в (10ю20) могут быть статистически независимы. При этом (10.20) переходит в

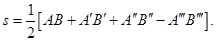
Значит универсальное соотношение (10.15):  уже не возникает и при отсутствии дополнительных условий величина  оказывается ограниченной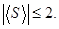

Часто при обсуждении неравенств Белла в качестве элементарных вероятностей выбирают не совместные распределения P(a, a¢, b, b¢ ), а другие вероятности вида Р(l), где l º {l₁, l₂...} - множество т.н. “скрытых” параметров. Эти параметры определяют неким причинным образом, например, по законам классической электродинамики, все свойства посылаемых сообщений. Следовательно, существуют некоторые однозначные зависимости вида а(l) и b(l). При этом предположение о нелокальности не используется! Приведенное выше доказательство остается в силе. Просто под усреднением надо понимать:

                                                                                     (10.21)

Здесь под интегралом стоит величина s(l), которая равна:

                            (10.22)

Эта величина опять зависит от четырех переменных и поэтому она ограничена s(l)= ± 1. Отсюда из условий

                                                                             (10.23)

снова получается (10.15): .

Предположение о существовании плотности распределения для скрытых параметров P(l) и однозначных причинных связей а(l) и b(l) подразумевает и существование совместного распределения P(a, a¢, b, b¢ ):

                                                                                  (10.24)

Здесь множество  - одно из 2⁴ = 16 непересекающихся множеств всего множества скрытых параметров L º {l}, порождающее причинным образом определенную комбинацию знаков a, a¢, b, b¢.

Таким образом ода приведенных вывода (со скрытыми параметрами и без) неравенства  предполагают возможность описания наблюдаемых эффектов в терминах элементарных вероятностей . Его невыполнение в квантовых моделях можно объяснять именно нарушением этой возможности. Такое же заключение можно сделать из появления отрицательных и многозначных вероятностей, рассчитываемых с помощью формулы   при использовании квантовых средних значений для произведений некоммутирующих операторов.

Итак, рассмотрим логику использующихся рассуждений в предположении о нелокальности:

1. Классические локальные ( в предположении о локальности, т.е. об отсутствии влияния аппаратуры на результаты измерения в другом канале) теории приводят к некоторым неравенствам.

2. Квантовая теория нарушает эти неравенства.  Отсюда делается вывод, что

3. квантовая теория нелокальна.

Этот вывод противоречит правилам формальной логики:

для сравнения рассмотрим аналогичный силлогизм:

1. Все хорошие анекдоты - короткие

2. Этот рассказ - длинный. Значит (?!),

3. этот рассказ - плохой.

Предсказания квантовой теории.

Для вывода соотношения типа (10.20) необходимо рассмотреть конкретную модель и конкретные квантовые состояния по которым будут производиться усреднения. Рассмотрим процесс параметрического рассеяния света из двух кристаллов, которые возбуждаются когерентной накачкой. Коррелированные фотоны вылетают одновременно из двух кристаллов 1 и 2 в две пространственные моды. Один из фотонов задерживается при помощи линий задержки b или a. Моды, соответствующие сигнальному (холостому) излучению, родившемуся в разных кристаллах смешиваются на светоделителях, так что каждая пара детекторов А или В регистрирует только сигнальное или только холостое излучение. Значит корреляция возможна только между детекторами А и В, и невозможна между А⁺ и А^- (В⁺ и В^-).

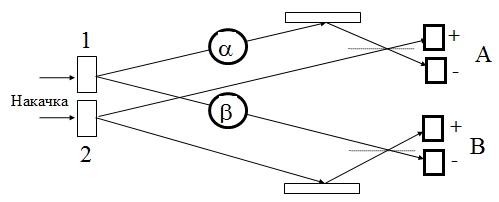
Предполагается, что сохраняется поперечный импульс:. В итоге получаем четырех-пучковую схему или схему для наблюдения двухфотонной интерференции. Итак сигнальные (холостые) пучки после светоделителя направляются на пару детекторов  и . Фазовая задержка a вводится в один из пучков. Аналогично строится вторая пара плеч. Светоделители преобразуют флуктуации фаз в флуктуации интенсивностей, которые регистрируются детекторами. Двухфотонная интерференция проявляется в том, что при наблюдении моментов четвертого порядка вида  они будут зависеть по гармоническому закону от суммарной фазы :

.

Видность интерференции интенсивностей при квантовом описании равна 100%. Теория скрытых параметров, которая рассмотрена выше дает оценку для видности:

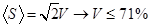
В классической теории видность ограничена уровнем 50%.

Пусть детекторы работают в режиме счета фотонов. Считаем, что число истинных совпадений намного превышает число случайных, которыми можно пренебречь. Если также предположить, что квантовая эффективность детекторов равна 100%, то детекторы с индексами А и В щелкают одновременно. Отсчет (фотон), зарегистрированный детектором   обязательно сопровождается отсчетом либо в детекторе , либо в детекторе . Параметризуем результаты измерения так, что когда щелкает детектор  переменная А принимает значение “+”, когда  - то “-“. И, наконец, введем третью дихотомную переменную - .

Среднее значение (первый момент) величины F:

                                                                              (10.25)

Здесь М - полное число испытаний.

Заметим, что наблюдатель, регистрирующий только события в “канале А” не замечает изменений показаний, вызванных вариациями фазовых задержек a или b. Вероятность принять значение “+” или “-“ для переменной А (как и В) одинакова:

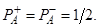
В то же время, из результатов экспериментов и расчетов по квантовой модели следует, что вероятность наблюдения “+” или “-“ значения переменной F:

                                                                   (10.26)

Совместное распределение вероятностей двух наблюдаемых А и В:

                                                                                      (10.27)

Тогда превышение числа коррелированных сигналов над антикоррелированными дается соотношением:

                                                          (10.28)

Более строгое выражение величины Е содержит множитель V, который имеет смысл видности интерференционной картины. В случае спонтанного параметрического рассеяния, когда мощность накачки мала и детекторы регистрируют лишь сопряженные моды (сигнальные и холостые), .

Пусть задержки, вносимые в канал А (или В) принимают два значения:

                                                                              (10.29)

Таким образом, в эксперименте исследуются сигналы в зависимости от четырех параметров: . Будем записывать результаты четырех серий экспериментов, соответствующих следующим парам значений параметров:

                                                                                   (10.30)

Из (10.25) следует, что анализируется четыре наблюдаемых величины:

                                                                          (10.31)

Назовем измеряемой Белла следующую комбинацию наблюдаемых величин:

                                                                (10.32)

После усреднения по М испытаниям, получим:

          (10.33)

В то же время, согласно квантовой теории (10.28, 10.29):

                        (10.34)

Замечание. В квантовой теории усреднение производится по перепутанному состоянию, которым является совместное состояние двух пар фотонов:

(конец)                                                (10.35)

Замечание. Можно показать, что квадрат наблюдаемой Белла определяется двумя коммутаторами:

(конец)                            (10.36)

Максимальное значение наблюдаемая Белла принимает для значений аргумента . Например, при :

Рекомендация для Вас - 19. Управление коммуникациями проекта.

                                                                        (10.37)

Видно, что оценка наблюдаемой Белла, выполненная в рамках квантовой теории дает величину, превышающую (в некоторых случаях) классическую величину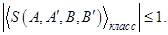

Замечание. Видно, что нарушение неравенства Белла происходит при значениях параметров, не соответствующих максимальным корреляциям. (конец)

Формально, нарушение неравенств Белла объясняется тем, что коммутаторы в (10.36) не равны нулю, т.е. невозможно одновременно измерить величины А и А¢ (В и В¢). В нашей модели это утверждение эквивалентно тому, что у фотона априори не существует одновременно двух фаз (или двух значений поляризации) одновременно. В каждой реализации можно измерить лишь одну фазу (поляризацию) фотона!

Если есть время, рассказать про парадокс ГХЦ, теорему Кохена- Шпехера, неравенства Клышко-Мермина.

ЛИТЕРАТУРА