Квантовые (неклассические) состояния света и их использование в квантовой информатике

ЛЕКЦИЯ 9. Квантовые (неклассические) состояния света и их использование в квантовой информатике.

1. Роль неклассических полей в физике квантовой информации. Определение (I) неклассического света и его недостатки.

2. Элементарная полуклассическая теория фотодетектирования. Фактор Фано и параметр группировки. Супер- и субпуассоновский свет. Одномодовый детектор. Формула Манделя. Гомодинирование. Связь распределений энергии и комплексной амплитуды. Квазивероятность. Распределение Глаубера-Сударшана.

3. Наблюдаемые признаки неклассичности света. Мера Ли. Операциональное определение (II) неклассического света. g₂ -  и D -критерии. Примеры: лазерный свет, тепловое излучение, смесь вакуумного и К-фотонного состояний.

Использование световых сигналов закономерно вызывает интерес при решении проблемы передачи квантовой информации. Дело в том, что определенные типы световых полей обладают рядом свойств, которые непосредственно используются в квантовых коммуникационных протоколах, например, таких как квантовая телепортация и сверхплотная кодировка. В квантовой криптографии сообщения между удаленными пользователями осуществляются на основе специфических световых полей, рассматриваемых как системы с квантовыми свойствами. Поэтому возникает вопрос количественного описания излучения и выделения его отличительных признаков. Особенно полезно выделить т.н. операциональные критерии, которые можно было бы применить в эксперименте. Грубо говоря, под неклассическим понимается свет, свойства которого нельзя описать классическим образом, т.е. такой свет, который не имеет классических аналогов.

Свойства световых полей можно исследовать анализируя свойства фототока, порождаемых ими. При этом логично анализировать как средний ток, так и его флуктуации. Известно, что средний ток пропорционален интенсивности света, падающего на фотодетектор. Флуктуации фототока можно объяснить случайностью рождения фотоэлектронов в процессе детектирования (фотоэффекта), поэтому долгое время им не придавали существенного значения. Такие флуктуации были названы пуассоновскими или дробовыми. Тривиальность флуктуаций такого рода объяснялась тем, что даже абсолютно стабилизированное по амплитуде и фазе электромагнитное излучение, которое описывается плоской волной, будет вызывать случайные флуктуации тока, вызванные случайностью рождения фотоэлектронов.

            Наблюдение флуктуаций фототока, превышающими по величине пуассоновские флуктуации было выполнено Брауном и Твиссом в середине 50-х годов. В этих экспериментах исследовался свет, излучаемый звездами или ртутной лампой. (Избыточные флуктуации наблюдались с помощью двух детекторов, т.е. в этих экспериментах анализировались четвертые моменты поля.) Такие избыточные флуктуации имеют объяснение в классической теории: поскольку амплитуда электромагнитной волны. падающей на детекторы случайно изменяется, то и флуктуации фототока также будут иметь дополнительную (по отношению к пуассоновскому уровню) синхронно изменяющуюся компоненту. В этом случае говорят о группировке фотонов в пучке, приводящей к суперпуассоновской статистике тока. Следовательно и свет, исследовавшийся Брауном и Твиссом, впоследствии названный тепловым, можно отнести к разряду “классических”. Тем не менее, эксперименты, выполненные Брауном и Твиссом, считают первыми экспериментами, положившими начало квантовой оптике.

Несколько позже были исследованы и истинно неклассические состояния поля, такие как излучение при двухквантовых переходах в атомах или спонтанном параметрическом рассеянии света. Еще позднее был зарегистрирован свет, у которого флуктуации тока оказались ниже, чем пуассоновский уровень - это эффект антигруппировки фотонов, приводящий к субпуассоновской статистике фототока или сжатые состояния.

С помощью неклассических состояний света стало возможным продемонстрировать известный парадокс, рассмотренный А.Эйнштейном, Б.Подольским и Н.Розеном, поскольку именно в таких состояниях реализовывались необходимые корреляционные свойства излучения. Впоследствии эти же состояния были использованы в экспериментах по нарушении неравенств Белла. Это позволило говорить о неприменимости классических моделей, в которых вероятностная интерпретация квантовой теории обосновывалась введением скрытых параметров.

Рекомендуемые материалы

Перед тем, как перейти к количественному описанию нелассических полей, заметим, что многие из  них образуются в результате нелинейных оптических процессов.

Замечание. В квантовой криптографии используется метод получения “однофотонных” состояний, который осуществляется с помощью ослабления лазерных импульсов. При этом, конечно возникающие состояния не являются однофотонными - всегда существует вероятность, что в импульсе окажется 0 или, скажем, 2 фотона.

Определение I. Свет, для которого Р-распределение Глаубера-Сударшана принимает отрицательные значения или является нерегулярной функцией, называется неклассическим. Здесь под Р-распределением понимается квантовый аналог классического распределения вероятности для амплитуд поля. 

Это определение, очевидно, нельзя отнести к непосредственно применяемым в эксперименте, т.е. операциональному. В экспериментах измеряется статистика фототока (или распределение импульсов фототока), связанная со статистическими свойствами падающего на детектор светового поля посредством формулы Л.Манделя.

Будем считать, что фотодетектор работает в “режиме счета фотонов”, когда на его выходе образуется последовательность не перекрывающихся импульсов фототока. Периодически подсчитывается число таких импульсов m за малое время Т. В силу случайности, это число флуктуирует - можно вычислить моменты, т.е. определить полные вероятностные характеристики дискретной случайной величины m. Зададим их с помощью распределения вероятностей , когда выполняются требования колмогоровской теории вероятностей                                                         (9.1)

или моментов:

                                                                    (9.2)

По определению, средним числом отсчетов и дисперсией называются моменты:

                                                                                            (9.3)

                                                                                 (9.4)

Через них можно определить ввести фактор Фано:

                                                                                                  (9.5)

и параметр группировки фотонов:

.                                                                (9.6)

Нетрудно заметить, что эти два параметра характеризуют отличие статистики от пуассоновской. Действительно, в случае пуассоновской статистики , поэтому . Для теплового поля , поэтому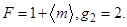

Если F < 1  или g₂ < 1, то статистика является субпуассоновской, а излучение - субпуассновским (неклассическим) светом или антигруппированным светом.

С точки зрения простейшей “корпускулярной” модели фотоэффекта эффект антикорреляции можно объяснить следующим образом. Пусть квантовая эффективность детектора h = 100%. Тогда прибытие каждого фотона вызывает появление фотоэлектрона. Таким образом поток фотоэлектронов “повторяет” поток фотонов, т.е. условие  означает, что в потоке фотонов имеется некая регулярность, по сравнению с хаотическим пуассоновским распределением, где все события равноправны. Тогда условие g₂ > 1 интерпретируется как группировка, а g₂ < 1 - как отталкивание. Например, известен способ получения антигруппированного света, когда одиночные атомы возбуждаются резонансным излучением, после чего они флюоресцируют. Акт следующего поглощения атомом энергии не может произойти раньше некоторого времени, поэтому и в излученном свете фотоны антигруппированы, что и дает субпуассоновскую статистику. В идеальном случае атом излучает в строго определенные моменты времени, поэтому

. Заметим, что в рамках корпускулярной модели света (фотоны- шарики) эффект антикорреляции имеет простое объяснение.

При использовании квантовых моделей для описания света число фотонов является оператором:

.                                                                                                        (9.7)

Можно рассчитать распределение числа фотонов p_n и моменты этого распределения . Последовательное квантовое описание очень хорошо согласуется с экспериментом, но встречаются трудности с его интерпретацией. Так, на сегодняшний день общепринятой является “копенгагенская” трактовка, которая не допускает априорного существования некоторых физических величин. Операциональные свойства неклассического света возникают в рамках полуклассического подхода, когда атомы детектора описываются квантовым образом, а падающее поле - классическим. В рамках этого подхода не удается описать ряд оптических экспериментов. Именно в этих случаях и принято говорить о неклассических состояниях света.

Одномодовый детектор.

Пусть площадь детектора А<<A_coh падающего света, а интервалы выборки . Таким образом детектор регистрирует одну моду поля, т.е. одну независимую колебательную степень свободы. Динамическое (или статистическое) описание  тогда совпадает с описанием гармонического осциллятора. Для стационарного квазимонохроматического поля

,

где Е₀ и  - случайные (медленно меняющиеся) функции времени. Характерное время изменения этих параметров и называется временем когерентности .

Замечание. Если детектор многомодовый, то необходимо дополнительно проводить усреднение по времени и пространству, что в пределе многих мод дает опять тривиальную пуассоновскую статистику, которая не зависит от свойств падающего поля.(конец)

Если от амплитуды перейти к числу фотонов - энергии, приходящейся на объем когерентности (в нашем случае ) и деленный на энергию одного фотона:

                      (9.8)

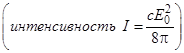
Эта величина принимает любые действительные неотрицательные значения. Поэтому и статистика фотоэлектронов в полуклассическом случае определяется непрерывным распределением Р(n).

Замечание. В квантовой теории этой классической переменной соответствует оператор числа фотонов в одной моде , который имеет спектр собственных значений в виде набора целых чисел 0, 1, 2... Статистика определяется дискретным распределением р(n). (конец)

Замечание. Среднее число фотонов в одной моде связано с интенсивностью I эффективной полосой частот света Dw (для одной поперечной моды):

 (конец)

В качестве примера рассмотрим световой поток, который имеет мощность

W = 10^-9 Вт, спектральная ширина излучения Df = Dw/2p = 10⁹ Гц с центральной длиной волны l = 0.5мкм. Тогда, подставляя в (9.8), получаем:

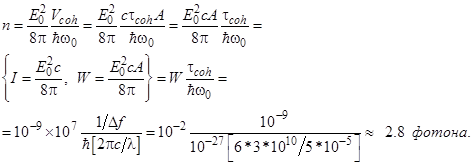
Формула Манделя (полуклассическая)

Если квантовая эффективность детектора равна h, то вероятность появления фотоэлектрона в интервале (t, t + dt). Поскольку фотоэлектроны рождаются случайно, то среднее их число за время Т:

 где символ m относится к электронам, а n - к фотонам. Если интенсивность поля постоянна, то n не флуктуирует. Будем считать детектор идеальным, т.е. h = 100%. Поскольку все моменты времени рождения фотоэлектрона эквивалентны, то он может с одинаковой вероятностью <n>dt/T возникнуть в любом интервале dt, принадлежащем Т. Тогда статистика числа отсчетов будет определяться распределением Пуассона:

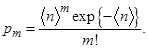                                                                                 (9.9)

Формула (9.9) показывает, что в среднем за время Т наблюдается m отсчетов. Для примера, разобранного выше () получаем: р₀ = 0.08, р₁ = 0.2, р₂ = 0.26, р₃ = 0.21, р₄ = 0.13, р₅ = 0.07 (для чисел m = 0, 1, 2, 3, 4, 5,...)

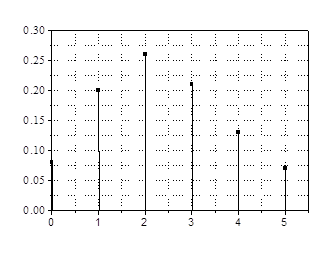
Замечание. Даже для стабилизированного по амплитуде излучения с E₀ = сonst (идеального лазера) имеем пуассоновское распределение фотоэлектронов - т.н. дробовой шум. (конец)

Все другие источники света, у которых величина n=<n> флуктуирует, будут характеризоваться избыточными флуктуациями фототока, вызванными флуктуациями интенсивности. Такие флуктуации можно описать, введя функцию распределения “интенсивности”: P(n). Т.е. вероятность того, что интенсивность излучения (выраженная в единицах n) принимает значение в интервале (n, n + dn) равна P(n)dn. Очевидно, что классическая плотность вероятности P(n) должна удовлетворять аксиомам Колмогорова:

                                                                              (9.10)

Тогда распределение наблюдаемой дискретной величины p_m оказывается связанным с распределением интенсивности поля P(n) через преобразование Пуассона:

                                                                   (9.11)

Наблюдается как бы двойная стохастичность. Во-первых, за счет случайности образования фотоэлектрона (постоянная величина - электромагнитное поле - порождает дискретный набор фотоэлектронов). Во-вторых, за счет флуктуаций самой интенсивности падающего света, что и приводит к избыточному шуму.

Тепловой (хаотический) свет.

Свет с тепловой статистикой возбуждается многими независимыми источниками со случайными амплитудами и фазами. Примером служит излучение нагретого тела, свет звезд. При этом распределение комплексной амплитуды  является гауссовым (или нормальным) с независимыми  и . Распределение интенсивности описывается экспоненциальным законом:

                                                                            (9.12)

Видно, что средняя интенсивность <I> полностью определяет статистику одной моды стационарного хаотического поля. Из (9.12) следует связь между дисперсией и средней интенсивностью:

                                                                 (9.13)

Для фотоотсчетов при этом справедливо:

                                                                         (9.14)

Гомодинное детектирование.

До сих пор рассматривалось лишь распределение энергии (интенсивности) падающего поля P(n)  и игнорировались флуктуации фазы j. Их можно измерить с помощью гомодина, смешивая исследуемое излучение с излучением стабильного по фазе лазерным пучком (т.н. опорный генератор). Пусть комплексная амплитуда волны.

По определению когерентными состояниями  называются собственные функции (неэрмитова) оператора уничтожения фотона:

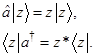
Замечание. Из этих формул сразу следует, что среднее число фотонов в когерентном состоянии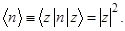

Связь между n и z дается условием нормировки:

                                                                                         (9.15)

Двумерная вероятность P_z(z)  полагается нормированной

, где .                                                                    (9.16)

Функция P_z(z) играет роль квазивероятности вероятности того, что осциллятор имеет комплексную амплитуду z, т.е. .

Тогда формула Манделя (9.11) приобретает вид:

                                                                      

Эту формулу называют квантовым аналогом формулы Манделя.

Замечание. Если квантовая эффективность меньше 100%, то (9.17) переходит в:

 (конец)                                    (9.17)

Можно выразить распределение энергии            P(n) через распределение комплексной амплитуды Тогда

                                    (9.18)

В случае стационарного поля P_z не зависит от фазы, следовательно,                                                                                             (9.19)

При гомодинировании (смешении) двух независимых по фазе колебаний распределение результирующего поля равно свертке исходных распределений:

                                                                      (9.20)

Одно из этих колебаний описывает лезерное поле со стабильной амплитудой z₀:

                                         (9.21)

Тогда  Теперь наглядно видно, что при гомодинировании исходное распределение  просто смещается в комплексной плоскости z без изменения своей формы! Согласно “Определению I” статус состояния не меняется - классическое распределение остается классическим, а неклассическое - неклассическим!

Замечание. Функция P_z(z) может принимать отрицательные значения и даже в случае чистого состояния  координата q и импульс p испытывают нулевые флуктуации, поэтому функцию P_z(z)  называют квазивероятностью. (конец)

            Используя формулу (9.17) можно найти распределение числа отсчетов для теплового и когерентного излучений.

1. Когерентное поле. , откуда

.

2. Тепловое поле. , откуда

где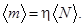

Квантовая теория.

В квантовой теории статистика  фотоотсчетов определяется оператором плотности r для свободного поля, падающего на детектор. При использовании (дискретного) фоковского базиса диагональный матричный элемент (детектор считается идеальным) дает вероятность наблюдения n отсчетов:

                                                                                     (*)

В случае чистого состояния  так что

Обычные моменты определяются в соответствии с правилами квантовой теории:

Что же общего между квантовой формулой (*) и полуклассической формулой Манделя (9.11)? Оказывается связь между вероятностью и матрицей плотности  просто преобразуется к виду (9.11). Для этого надо использовать непрерывное представление векторов и операторов по когерентным состояниям . При этом оператор плотности изображается некоей функцией, называемой представлением Глаубера-Сударшана. Эта функция определяет распределение отсчетов p_m посредством преобразования Пуассона, совпадающим по форме с формулой Манделя (9.11) или (9.17). Отличие состоит только в том, что функция P_z(z) или  определена  теперь через оператор плотности и может быть отрицательной и нерегулярной, т.е. является квазираспределением.

Наблюдаемые признаки неклассического света.

Только что было продемонстрировано, что свойство неклассичности инвариантно к гомодинированию с когерентным состоянием (лазерное поле с постоянной комплексной амплитудой). Оказывается, что это утверждение не выполняется в случае подмешиваемого поля с произвольной статистикой, например, с тепловой. Такое поле (тепловое) имеет экспоненциальное распределение интенсивности. Поэтому исходное распределение “портится” тем быстрее, чем больше интенсивность теплового поля. При этом сингулярные и отрицательные участки исчезают, так что исходное неклассическое поле может стать классическим.

Мера Ли.

Пусть N_T - среднее число фотонов в одной моде вспомогательного теплового поля. Под мерой Ли понимают минимальное число фотонов, N₀ = N_T, при котором распределение P_z(z) остается неотрицательной регулярной функцией в смысле “Определения I”. Можно показать, что N₀ изменяется от 1 (для максимально неклассических полей - К-фотонных) до 0 (для классических). Важно то, что величину N₀ можно, в принципе, измерить. Для этого следует к исследуемому свету добавить с помощью светоделителя тепловой свет с регулируемой интенсивностью.

Операциональное определение неклассического света.

Для идеального лазера, статистика которого описывается распределением Пуассона, .Следовательно, для такого излучения F = g₂ = 1. Поэтому представляется, что другие источники света из-за нестабильности их параметров могут лишь увеличить шумы фототока. Отсюда следует вывод, что наблюдение субпуассоновской статистики с g₂ < 1 в полуклассической теории невозможно! Значение g₂ = 1 является нижней границей в случае полуклассической теории фотоотсчетов: g_{2 class} = 1. Условие g₂ < 1 также называют g₂ - критерием неклассичности света.

Определение II. Если наблюдаемая статистика фотоотсчетов не согласуется с полуклассической формулой Манделя (9.11) при P(n) ³ 0, т.е. если падающий на детектор свет нельзя описать некоторым распределением энергии P(n), то свет называется неклассическим.

Замечание.  Если свет порождает антигруппировку отсчетов, то он неклассичен.

Как же применить “Определение II” к результатам эксперимента? Очевидно, для этого нужно обратить формулу Манделя (9.11), т.е. определить функцию P(n) через измеренный набор чисел {p_m}. Если это удастся, то проверить условие неотрицательности P(n) ³ 0.

В общем случае эта процедура неоднозначна. Она восходит к математической проблеме моментов - выражение вероятностей через моменты, которая рассматривалась на прошлой лекции.

Пусть в эксперименте измерен набор (чисел) отсчетов {m}. Из них можно построить наборы вероятностей {p_m} или факториальных моментов:

                                                        (9.22)

Они являются комбинациями обычных моментов <m^k> , например,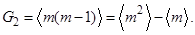

Замечание. Если известны обычные моменты <mⁱ> для 1 £ i £ k, то можно вычислить и факториальные G_k. (конец)

Замечание. Факториальные моменты дискретного распределения отсчетов p_m, определяемого по формуле Манделя (9.11) совпадают с обычными моментами непрерывного распределения энергии P(n):

(конец)                                                                     (9.23)

Замечание. Нормированные факториальные моменты вводятся так:

(конец)                                                                                         (9.24)

Из чисел отсчета {m_k} можно составить комбинации моментов G_k некоторой неотрицательной функции, следовательно, моменты должны удовлетворять некоторым неравенствам.

Оказывается, что в общем случае для неклассичности света достаточно выполнение хотя бы одного из бесконечного набора условий вида .                                                                                        (9.25)

Замечание. Выполнение условий (9.25) является достаточным условием, т.е. при невыполнении ни одного из этих условий свет может быть неклассическим. Необходимым условием классичности служит неравенство:

В частности, при k = l, получаем:

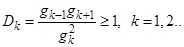
Например, при k = 1, .

Итак, упомянутые выше неравенства имеют вид:

                                                                        (9.26)

.                                                                                              (9.27)

Эти условия называются D_k - критериями. Рассмотрим, например,  условие D₁(0) =g₂ < 1. Оно совпадает с наиболее известным критерием неклассичности - антигруппировкой фотоотсчетов. Условие D_k(0) < 1 при  иногда называют антигруппировкой высших порядков. Введенные величины могут служить и количественными мерами степени неклассичности. Так случай D_k = 0 соответсвует максимальной неклассичности, а D_k = 1 - минимальной. Рассмотрим некоторые примеры.

1. Идеальный лазерный свет дает пуассоновское распределение числа отсчетов (9.9) с параметром <n> = N = |z₀|²:

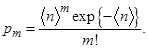
При этом g_k = G_k = N^k . Поэтому D_k (0) = D_k (1)= 1. Это распределение является промежуточным между классическим и квантовым.

2. Тепловое поле дает

                                                  

откуда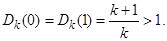

3. Рассмотрим такие распределения числа отсчетов для которых вероятность некоторого числа отсчетов к равна нулю:  Тогда

 - распределение неклассично.

Аналогично, если , то .

Возникает вопрос, не исчерпывает ли условие антигруппировки g₂ < 1 (или g₂  -критерий) все случаи неклассического света, т.е. не является ли это условие достаточным?

Рассмотрим в качестве примера шумовое излучение вырожденного по частоте параметрического усилителя света - параметрическое рассеяние света. Состояние света при этом называют сжатым вакуумом. Из квантовой теории следует, что  и . Здесь Г - коэффициент параметрического усиления, который зависит от расстройки синхронизма, c⁽²⁾, интенсивности накачки и проч. Тогда

                                                                             (9.28)

Следовательно статистика параметрического рассеяния - сверхпуассоновская, и согласно g₂-критерию свет является классическим! Более того, обычно в эксперименте g₂ ~ 10² - 10⁸ и имеет место сверхгруппировка, когда g₂ > 2. Именно такое излучение часто используется в квантовых коммуникационных протоколах. Почему же его относят к неклассическим?

Теоретически это следует из “Определения I”. Можно показать, что регулярного P_z- распределения Глаубера Сударшана не существует.

С другой стороны, расчет матрицы плотности дает значения ее диагональных компонент r_nn = 0 для нечетных n. Таким образом, сжатый вакуум состоит четного числа фотонов, когда p_2k+1 = 0. Такие резкие провалы в распределении вероятностей противоречат полуклассической формуле Манделя (9.11), согласно которой соседние вероятности  должны иметь, по-видимому, сравнимые величины. Это подтверждается и D-критериями (9.26, 9.27): при четных m получаем

.

Излучение при параметрическом рассеянии света неклассично, даже при отсутствии антигруппировки! В предельном случае Г<<1 параметрический усилитель излучает смесь вакуумного (преобладающего) состояния и двухфотонного фоковского:

Среднее число фотонов  и моменты можно выразить через него. .              (9.29)

В случае  получаем чистое энергетическое состояние с К фотонами, когда в объеме когерентности заведомо присутствует К фотонов. В зависимости от соотношения между   и N  можно получить разные типы статистики К-фотонного света.

Из (9.29) следует, что параметр группировки для К-фотонного равен:

.                                                                                    (9.30)

1. Пусть  (смесь К-фотонного состояния и вакуума). Отсюда получаем сверхгруппировку, g₂ >>1.

Ниже изображено распределение числа фотонов для

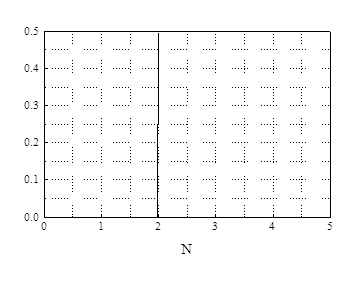
2. Пусть  получаем антигруппировку. В частности при однофотонном распаде (К = 1), g₂  = 0.

3. В чистом К-фотонном состоянии флуктуации числа фотонов N отсутствуют,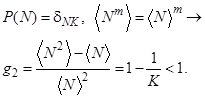

Если Вам понравилась эта лекция, то понравится и эта - Часть 40.

В заключение отметим, что излучение при параметрическом рассеянии света (смесь вакуума и двухфотонного света) используется для демонстрации более общей неклассичности света. Этот тип неклассичности противопоставляется не с классической статистической оптикой, а с вероятностной моделью, предложенной Беллом, основанной на наличии “скрытых” параметров у квантовых объектов.

На будущее: подробно остановиться на анализе неклассичности основных типов полей, используемых в квантовой информации: К-фотонных и их смеси с вакуумом (это есть); сжатых (этого почти нет), а также классических - тепловых и когерентных (это есть)

ЛИТЕРАТУРА.

1. Д.Н.Клышко. Неклассический свет. УФН, т.166, №6, 613-638 (1996).

2. Д.Н.Клышко. Квантовая оптика: квантовые, классические и метафизические аспекты. УФН, т.164, № 11, 1187-1214 (1994).

3. Д.Н.Клышко Физические основы квантовой электроники. М.,”Наука”, 1986, 293с.