Безмоментные оболочки вращения

Безмоментные оболочки вращения

         Для оболочек вращения часто используются сферические координаты R, ξ = , η = φ. Две последние определяют положение точки срединной поверхности. Угол отсчитывается от оси вращения, угол  φ - от некоторого фиксированного положения меридиональной плоскости.

         При таком выборе координат

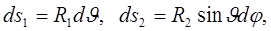
т.е.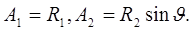

Для оболочки вращения радиусы кривизны зависят только от угла . Для радиусов кривизны существует связь, называемая условиями Кодацци:

.

С учетом независимости радиусов кривизны от φ уравнения равновесия оболочки вращения приводятся к виду

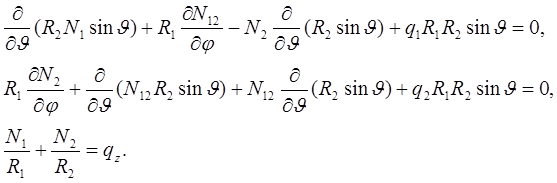
Рекомендуемые материалы

         После преобразований эти уравнения можно привести к такой форме:

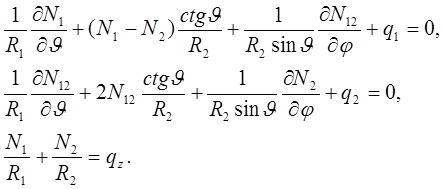
         Физические соотношения свой вид не меняют, и от выбора координат не зависят.

Геометрические имеют вид:

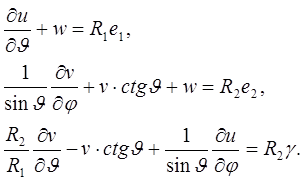
В случае осесимметричной нагрузки и соответственно осесимметричного деформирования во всех этих соотношениях исчезают производные по φ; кроме того, при q₂ = 0 исключается кручение оболочки, и тогда N₁₂ = 0. В итоге второе уравнение равновесия выполняется тождественно, а первое и третье принимают вид

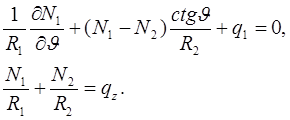
Из второго уравнения выразим N₂ и подставим в первое. Тогда с учетом соотношений Кодацци оставшееся уравнение примет вид

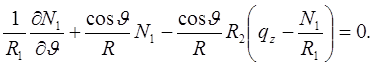
Помножим это уравнение на  учтем, что все величины зависят только от одной переменной, и можно перейти к обыкновенным производным, а также соотношения Кодацци. Тогда

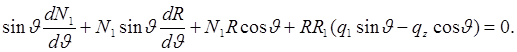
Это можно привести к легко интегрируемому виду

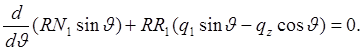
При отсутствии выреза в вершине оболочки интеграл будет

                 (*)

Если же есть вырез, то интегрирование ведется от координаты =₀, отвечающей краю выреза. Для определения постоянной С нужно задать граничное условие.

Из этого уравнения определяется N₁, затем легко находится N₂.

Механический смысл соотношения (*) легко усматривается после домножения его на величину 2π:

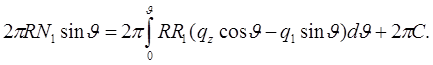
Если учесть, что  - это проекция погонного усилия на ось вращения оболочки, то слева – проекция суммы сил, возникающих в сечении оболочки с текущей координатой , а справа – сумма внешних нагрузок, приложенных к соответствующей части оболочки.

Пример

Определить усилия в сферическом куполе под действием собственного веса, если вес единицы площади купола равен q.

Для сферического купола и нагрузки

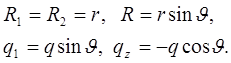
Из (*) определяется N₁:

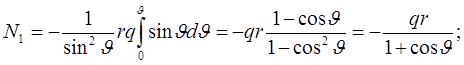
Затем определяется N₂:

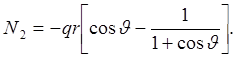
Следует отметить, что в вершине купола при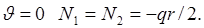

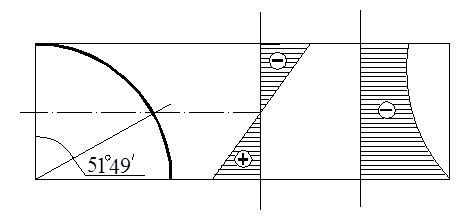
Если построить графики распределения этих усилий по высоте купола, то получится рис. 1:

                                                        N₂                    N₁

Рекомендация для Вас - Методы управления персоналом.

Из этих графиков следует, что существует некоторое значение координаты , при котором у окружного усилия N₂ меняется знак. Сжимающие усилия (отрицательные) переходят в растягивающие через ноль. Для определения этого значения угла необходимо в выражении для N₂ приравнять квадратную скобку нулю. Тогда получим

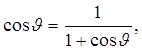
откуда _* = 51⁰49^/.

Эта линия представляет собой т.н. «шов перехода».

Если сферический купол будет опираться на основание как раз на уровне шва перехода, то в основании не будет возникать ни сжимающих, ни растягивающих напряжений. Во всех остальных случаях нужно основание подкреплять – либо набором тяг, работающих на растяжение (<_*), либо подкрепляющих ребер, работающих на сжатие (>_*)/