Усилия и моменты. Уравнения равновесия

Усилия и моменты. Уравнения равновесия

Элемент оболочки вырезается таким образом, чтобы нормальные сечения оболочки были направлены вдоль линий кривизны.

В произвольном слое на расстоянии z от срединной поверхности ненулевые напряжения обозначим , соответствующие значения в срединной поверхности записываются далее без верхнего индекса.

Усилия на части контура  вводятся по формулам

,

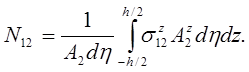
Если учесть зависимости коэффициентов Ламе, полученные для оболочки ранее, то

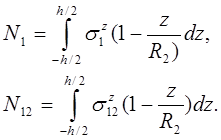
Аналогично вводятся усилия на части контура :

Рекомендуемые материалы

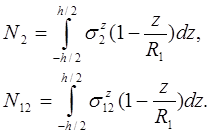
Размерность усилий сила/расстояние (Н/м). Для сравнения: силы измеряются в Н, напряжения в Н/м² = Па.

Изгибающие и крутящие «погонные», т.е. распределенные, моменты, вводятся по формулам

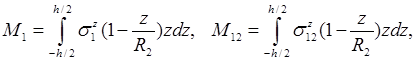
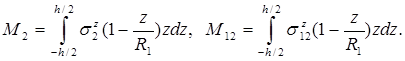
Размерность этих величин – Н, хотя правильнее было бы говорить о размерности Н·м / м.

Если считать, что то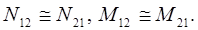

В сечениях вводим так называемые поперечные силы  Кроме того, считаем, что на единицу элемента оболочки действуют распределенные нагрузки вдоль осей q₁, q₂, q_z.

При составлении уравнений равновесия учтем, что в них входят не усилия или напряжений, а силы. Кроме того, учтем, что длины дуг, вырезающих элемент оболочки, по одной паре смежных сторон

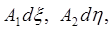
а по другой

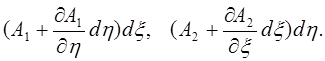
Кроме того, в криволинейных координатах у вырезанной координатными линиями элементарной площадки противоположные стороны в общем случае не параллельны друг другу.

Подробно распишем уравнение равновесия вдоль касательной к линии ξ:

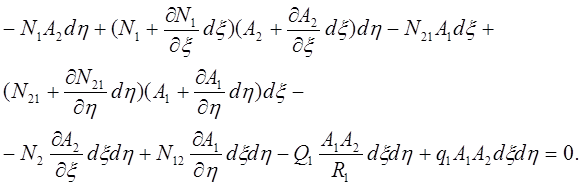
Два первых слагаемых в последней строке появляются за счет непараллельности сторон элемента оболочки. Последнее слагаемое – распределенная внешняя нагрузка.

После приведения подобных и отбрасывания слагаемых высшего порядка малости получим первое и второе по аналогии уравнения равновесия

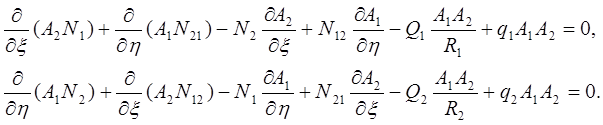
В проекции на нормаль к срединной поверхности оболочки третье уравнение равновесия приводится к виду

В лекции "3.16 Наука и просвещение, книжное дело и периодика" также много полезной информации.

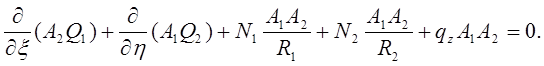
         Аналогично получаются два уравнения равновесия моментов, когда вектор-моменты проецируются на оси в срединной поверхности

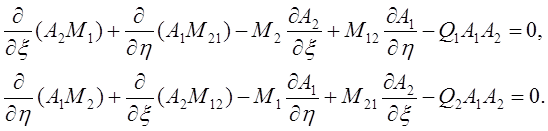
         Наконец, проецируя вектор-моменты на нормаль, получим

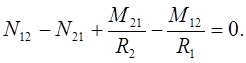
         Обычно принимается, что это последнее уравнение выполняется тождественно. Оценки погрешности возникающей неточности показывают, что они не превышают отношения h/R по сравнению с единицей.