Динамика простейших движений твердого тела

Лекция 4. Динамика простейших движений твердого тела

4. 1. Основные задачи динамики твердого тела

В статике были рассмотрены условия равновесия системы сил, приложенных к абсолютно твердому телу и условия, при которых твердое тело находится в покое. Задание уравнений движения твердого тела и определение скоростей и ускорений точек твердого тела было рассмотрено в кинематике. При решении задач динамики твердого тела встают более сложные задачи, которые делятся на две основные группы. К первой группе относятся задачи, в которых по заданным уравнениям движения твердого тела требуется определить систему сил, под действием которых происходит это движение. Ко второй относятся задачи, в которых по заданным силам, действующим на тело, требуется при определенных начальных условиях найти уравнения движения тела, а для несвободного тела найти также реакции связей.

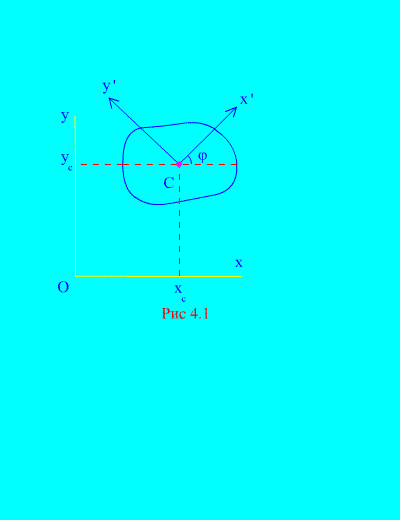
Рассмотрим движение твердого тела в плоскости. Для определения его положения требуется задать три независимых между собой параметра. Обычно это координаты центра масс ,  и угол поворота , который составляет ось х с осьюна теле  (рис. 4.1). Очевидно, что координаты центра масс ,  и угол   полностью определяют положение твердого тела в плоскости.

Движение тела в плоскости обычно раскладывают на простейшие: поступательное движение тела, задаваемое уравнениями движения  центра масс   и вращение тела вокруг оси, проходящей через центр масс тела, задаваемое уравнением

Для получения законов движения воспользуемся теоремой о движении центра масс и теоремой об изменении кинетического момента.

Согласно теореме о движении центра масс (3.6), имеем

Рекомендуемые материалы

, т.е.  .

Здесь m – масса тела, главный вектор внешних сил. Если тело не свободно, реакции связей считаем внешними силами.

Используя теорему об изменении кинетического момента относительно оси Оz, перпендикулярной плоскости вращения Оху (3.18, а), имеем

Здесь  кинетический момент тела, главный момент внешних сил.

Итак, законы движения тела в плоскости имеют вид

                                                         (4.1)

4.2.Дифференциальные уравнения поступательного движения твердого тела

Для того, чтобы твердое тело двигалось поступательно, линия действия главного вектора внешних сил должна проходить через центр масс тела. Тогда угловая скорость и, соответственно, кинетический момент тела равны нулю.

Пусть тело движется поступательно, уравнения движения имеют вид: , а угол  (рис. 4.1). Тогда проекции дифференциального закона, описывающего поступательное движение твердого тела в плоскости, согласно (4.1), имеют вид

.                                     (4.2)

Дифференциальный закон (4.2)  имеет форму закона движения материальной точки в плоскости и в  общем случае позволяет решить две основные задачи динамики:

· первая задача: по заданным уравнениям движения центра масс  и , вычисляя вторые производные по времени и, используя (4.2), находят проекции главного вектора внешних сил  и ;

· вторая задача: по заданным  и  и начальным условиям задачи (при  заданы значения ), определяют  уравнения  движения центра масс:  и ; методы интегрирования полностью аналогичны методам интегрирования дифференциальных уравнений прямолинейного движения точки.

4.3. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси

Твердое тело, вращающееся вокруг неподвижной оси, является примером несвободного твердого тела. Следовательно, при изучении его движения необходимо (применив аксиому связей) отбросить связи и, заменив их реакциями связей, рассматривать твердое тело как свободное.

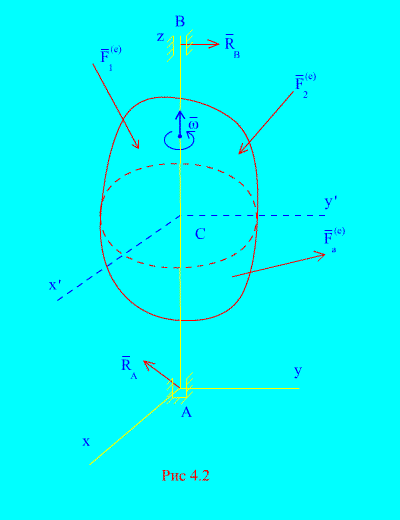
Рассмотрим вращение тела относительно неподвижной оси z, проходящей через центр масс (рис. 4.2). Тогда положение тела будет определяться углом между плоскостями zAх и(оси x,y – неподвижны; оси - связаны с телом и вращаются вместе с ним). Для нахождения закона, описывающего вращение тела вокруг неподвижной оси, воспользуемся законом движения свободного тела в плоскости (4.1). Поскольку , имеем

                                    (4.3)

Здесь главный момент внешних сил. При  вращении твердого тела вокруг неподвижной оси, согласно (3.16), кинетический момент

,

где  - постоянный для твердого тела момент инерции относительно оси вращения; - угловая скорость вращения. Учитывая это, получаем из (4.3)

.                                                   (4.3а)

Известно, что , тогда

 .                                                          (4.4)

Это и есть дифференциальный закон вращения твердого тела вокруг неподвижной оси z. Реакции подшипников  и  считаем внешними силами (отметим, что они не создают моменты относительно оси вращения,  т.к. линии их действия пересекают эту ось).

В частном случае, когда

,       то        ,

т.е. вращение тела происходит с постоянным угловым ускорением. Такое вращение называется равнопеременным вращением.

Если  ,  то .

 Это случай равномерного вращения тела, т.е. вращения тела по инерции.

Дифференциальное уравнение (4.4) в общем случае позволяет решить две основные задачи динамики:

· первая задача связана с дифференцированием: по заданному уравнению вращения тела  определяют главный момент внешних сил.

· вторая задача связана с интегрированием уравнения (4.4): по заданному главному моменту  внешних сил  и  начальным условиям задачи, находят уравнение вращения тела .

4.3.1. Физический маятник. Математический маятник

Физическим маятником называется твердое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси в поле сил тяжести.

 (рис. 4.3). Проведем через центр масс тела С плоскость, перпендикулярную оси вращения. Точка пересечения О этой плоскости с осью вращения называется точкой подвеса. Примем эту точку за начало координат. Оси х и у расположим в плоскости, проходящей через центр масс и точку подвеса, ось z направим по оси вращения (перпендикулярно плоскости xoy).

Дифференциальный закон вращения тела вокруг оси z, согласно (4.4), запишется

.                                                        (4.5)

Здесь  - момент инерции тела, относительно оси, проходящей через точку подвеса;  - угол между неподвижной осью х и линией ОС (рис. 4.3).

Так как в этом случае

                                               ()

здеь m – масса тела; а – расстояние от точки О до центра масс (а);  - момент инерции тела относительно оси , проходящей через центр масс С.

Дифференциальное уравнение вращательного движения тела (4.5) c учетом  () примет вид

                              (4.5а)

Знак минус в уравнении означает, что момент силы тяжести направлен против увеличения угла . Если угол отклонения мал, то с большой точностью можно считать , тогда уравнение (4.5а) перепишется в виде

.              (4.6)

Полученное уравнение совпадает по форме с дифференциальным уравнением свободных колебаний точки и его общим решением будет

Полагая, что в начальный момент t=0 маятник отклонен на малый угол  и отпущен без начальной скорости (), найдем для постоянных интегрирования значения А₁=0,А₂=, тогда .

Маятник совершает колебания с малой амплитудой, частота и период которых определяются формулами

(4.7)

Такие колебания называются гармоническими, а уравнение (4.6) называется уравнением гармонических колебаний.

Пусть физический маятник состоит из материальной точки массой m, подвешенной на невесомой нити длиной а и колеблющейся около точки подвеса О. Такой маятник называется математическим. Поскольку момент инерции материальной точки относительно оси z, проходящей через центр С равен нулю, т.е. , из (4.7) находим частоту и период колебаний математического маятника:

.                                       (4.8)

Сравнение формул (4.7) и (4.8) показывает, что период колебаний математического маятника меньше периода колебаний физического маятника той же длины.

4.3.2. Экспериментальное определение моментов инерции

Рассмотрим определение момента инерции тела способом крутильных колебаний. Тело подвешивают на упругом стержне или струне так, чтобы центр масс тела лежал на продолжении оси стержня (рис. 4.4). Закрутив стержень, жестко связанный с телом, на малый угол , измеряют период колебания системы.

Так как при малом угле закручивания момент упругих сил пропорционален этому углу, то дифференциальное уравнение крутильных колебаний системы имеет вид

где k – постоянный коэффициент, характеризующий упругие свойства струны (стержня).

Частота и период колебаний, очевидно, будут

.                                      (4.9)

Затем на тот же стержень подвешивают тело (например, диск), момент инерции которого относительно оси ОС известен и равен , и измеряют период колебаний  в этом случае.

Период колебаний определяется аналогично (4.9):

.                                                 (4.10)

Исключая в равенстве (4.9) и (4.10) неизвестный коэффициент k, получим формулу для определения момента инерции

.

4. 4. Плоское движение твердого тела

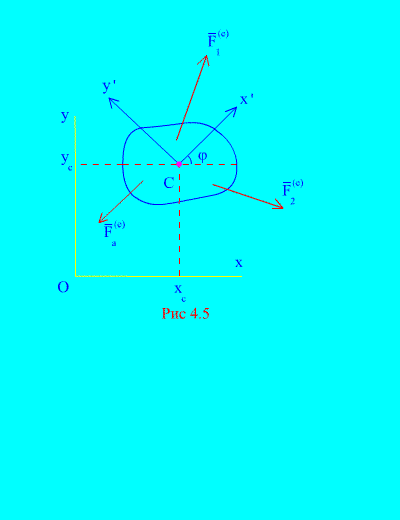
При  плоском движении все точки твердого тела движутся  в параллельных плоскостях. Поэтому достаточно рассмотреть движение какого-либо сечения тела в одной плоскости (рис. 4.5).

В соответствии с (4.1) имеем

Cогласно (3.16), кинетический момент твердого тела  , тогда дифференциальный закон плоско – параллельного движения примет вид

     (4.11)

где m – масса тела,  - момент инерции твердого тела относительно оси вращения,  главный момент внешних сил относительно оси вращения.

Если тело совершает несвободное движение, то в число внешних сил следует включить реакции связей.

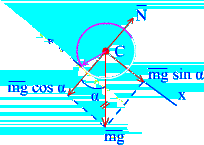
4.4.1.Скатывание цилиндра с наклонной плоскости

Будем считать, что скатывание цилиндра радиусом R происходит без скольжения. Силы, действующие на цилиндр, указаны на (рис. 4.6). Сила Т – сила сцепления, которая обеспечивает скатывание цилиндра. Ось х удобно направить вдоль наклонной плоскости. Напишем законы движения, имея в виду, что через точку С проходит мгновенная ось вращения. Уравнения (4.11)  имеют вид

,    ,                   (4.12)

где ; отсчет направлений вращения выбран так, чтобы угловая скорость  () увеличивалась при скатывании цилиндра.

Вычисляя Т из второго уравнения (4.12) и подставляя в первое, учитывая, что , получим

,

Или

.               (4.13)

Таким образом, центр масс цилиндра движется с постоянным ускорением .

4. 4. 2. Маятник Максвелла

Маятник Максвелла представляет собой диск, подвешенный на нерастяжимой нити. Нить конечной длины намотана на ось диска и закреплена на оси (рис. 4.7). Уравнения движения маятника имеют вид

, ,                          (4.14)

где  - момент инерции всего диска относительно оси, проходящей через центр масс;  - радиус оси диска, на которую намотана нить; Т – сила натяжения.

Структура уравнений маятника Максвелла полностью аналогична структуре уравнений цилиндра, скатывающегося с наклонной плоскости (уравнения 4.12) и решаются аналогично.

Получаем из (4.14)

Откуда

                  (4.15)

Проследим динамику движения маятника. Ускорение диска всегда постоянно и направлено вниз. Его числовое значение тем меньше, чем больше момент инерции . При достаточно большом моменте инерции  диск будет иметь малое ускорение. В пределе , , а ; так и должно быть, потому что диск просто висит на нити без движения. При  сила натяжения нити . В этом случае диск свободно падает, и поэтому нить не испытывает никакого натяжения. Уравнения (4.14) и решение (4.15) не описывают поведение маятника в нижней «мертвой» точке. В этом положении центр масс диска испытывает большое ускорение. По третьему закону Ньютона, это приводит к большому натяжению нити. Если нить недостаточно прочна, то она может в этот момент порваться.

Рассмотрим еще один пример плоского движения тела.

Пример. На двух нерастяжимых невесомых нитях одинаковой длины подвешен в точке О однородный стержень АВ массой m и длиной 2L (рис. 4.8). Нити со стержнем образуют углы . В некоторый момент времени нить ОВ обрывается. Найти натяжение Т нити ОА непосредственно после момента обрыва.

Решение. Движение стержня после разрыва нити плоское. В момент разрыва ускорение центра находится по теореме об ускорениях при плоском движении. За полюс выберем точку А. Вычислим ускорение центра масс стержня АВ, т.е. ускорение точки С:

       (4.16)

здесь  - ускорение полюса А,  - ускорение центра масс при его вращении относительно полюса А. Поскольку точка А может двигаться только по окружности радиуса ОА, а ее скорость в момент обрыва нити равна нулю, то . Проекцию ускорения точки А по касательной обозначим .

Обозначим модуль углового ускорения стержня через , а модуль угловой скорости через  (начальный момент времени равен нулю). Тогда  и направлена вдоль стержня от точки С к точке А;  и направлена перпендикулярно стержню в точке А (рис. 4.9).

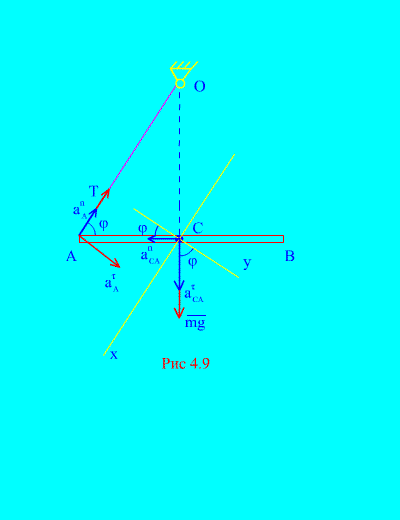
Выберем систему координат xСy, как показано на (рис. 4.9). Тогда ускорение точки  имеет следующие проекции на эти оси:

          (4.17)

Поскольку  закон плоского движения (4.11) с учетом (4.17) запишется

Ещё посмотрите лекцию "Нейропсихологические синдромы при локальных поражениях мозга" по этой теме.

 (4.18)

где учтено, что момент инерции стержня относительно его центра , равен .

Из третьего уравнения (4.18) выразим  и подставим в первое уравнение, получим

.

Отсюда находим

.