Общие теоремы динамики
Лекция 3. Общие теоремы динамики
Динамика системы материальных точек является важным разделом теоретической механики. Здесь в основном рассматриваются задачи о движении механических систем (систем материальных точек) с конечным числом степеней свободы – максимальным числом независимых параметров, определяющих положение системы. Главная задача динамики системы – изучение законов движения твердого тела и механических систем.
Наиболее простой подход к исследованию движения системы, состоящий из N материальных точек, сводиться к рассмотрению движений каждой отдельной точки системы. При этом должны быть определены все силы, действующие на каждую точку системы, в том числе и силы взаимодействия между точками.
Определяя ускорения каждой точки в соответствии со вторым законом Ньютона (1.2), получим для каждой точки три скалярных дифференциальных закона движения второго порядка, т.е. 3N дифференциальных закона движения для всей системы.
Для нахождения уравнений движения механической системы по заданным силам и начальным условиям для каждой точки системы, полученные дифференциальные законы нужно проинтегрировать. Эта задача трудна даже в случае двух материальных точек, которые движутся только под действием сил взаимодействия по закону всемирного притяжения (задача о двух телах), и исключительно трудна в случае трех взаимодействующих точек (задача о трех телах).
Поэтому необходимо отыскать такие методы решения задач, которые бы приводили к решаемым уравнениям и давали представление о движении механической системы. Общие теоремы динамики, являясь следствием дифференциальных законов движения, позволяют избежать сложности, возникающие при интегрировании и получать необходимые результаты.
3. 1. Общие замечания
Рекомендуемые материалы
Точки механической системы будем нумеровать индексами i, j, k и т.д., которые пробегают все значения 1, 2, 3…N, где N – число точек системы. Физические величины, относящиеся к k-й точке, обозначаются таким же индексом, что и точка. Например, 
, 
выражают соответственно радиус-вектор и скорость k-й точки.
На каждую из точек системы действуют силы двоякого происхождения: во-первых, силы, источники которых лежат вне системы, называемые внешними силами и обозначаемые 
; во-вторых, силы со стороны других точек данной системы, называемые внутренними силами и обозначаемые 
. Внутренние силы удовлетворяют третьему закону Ньютона. Рассмотрим простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии.
Первое свойство. Геометрическая сумма всех внутренних сил системы (главный вектор внутренних сил) равна нулю.
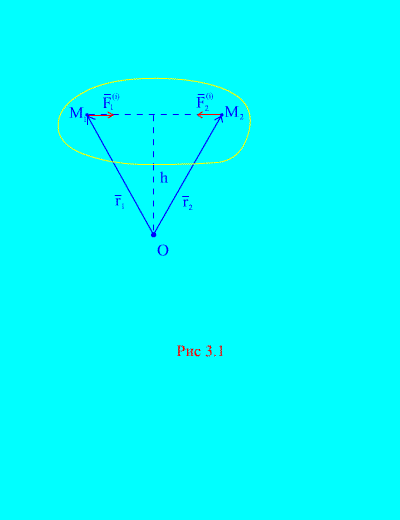
Действительно, если рассмотреть какие-либо две произвольные точки системы, например 
и 
(рис. 3.1), то для них 
, т.к. силы действия и противодействия всегда равны по модулю, действуют вдоль одной линии действия в противоположном направлении, которое соединяет взаимодействующие точки. Главный вектор внутренних сил 
состоит из пар сил взаимодействующих точек, следовательно
(3.1)
Второе свойство. Геометрическая сумма моментов всех внутренних сил относительно произвольной точки пространства равна нулю.
Рассмотрим систему моментов сил 
и 
относительно точки О (рис. 3.1). Из (рис. 3.1). видно, что
,
т.к. обе силы имеют одинаковые плечи и противоположные направления векторных моментов. Главный момент внутренних сил 
относительно точки О состоит из векторной суммы таких выражений и равен нулю. Следовательно,
.
(3.2)
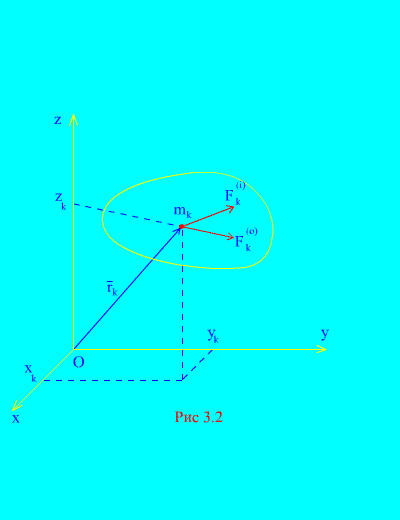
Пусть заданы внешние и внутренние силы, действующие на механическую систему, состоящую из N точек (рис. 3.2). Если к каждой точке системы приложить равнодействующую внешних сил 
и равнодействующую всех внутренних сил , то для любой k-й точки системы можно составить дифференциальные уравнения движения. Всего таких уравнений будет N:
, (3.3)
а в проекциях на неподвижные оси координат 3N:
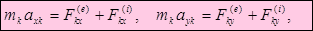
(3.4)
Векторные уравнения (3.3) или эквивалентные им скалярные уравнения (3.4) представляют дифференциальные законы движения материальных точек всей системы. Если все точки движутся параллельно одной плоскости или одной прямой, то число уравнений (3.4) в первом случае будет 2N, во втором N.
Пример 1. Два груза массой 
и 
связаны между собой нерастяжимым тросом, перекинутым через блок (рис. 3.3). Пренебрегая силами трения, а также массой блока и троса, определить закон движения грузов и натяжения троса.
Решение. Система состоит из двух материальных тел (связанных нерастяжимым тросом), движущихся параллельно одной оси х. Запишем дифференциальные законы движения в проекциях на ось х для каждого тела.
Пусть правый груз опускается с ускорением 
, тогда левый груз будет подниматься с ускорением 
. Мысленно освобождаемся от связи (троса) и заменяем ее реакциями 
и 
(рис. 3.3). Считая тела свободными, составим дифференциальные законы движения в проекции на ось х (имеется в виду, что натяжения нити являются внутренними силами, а вес грузов – внешними):
.
Поскольку 
и 
(тела связаны нерастяжимым тросом), получаем
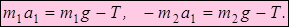
Решая эти уравнения относительно ускорения
и натяжения троса Т, получим
.
Отметим, что натяжение троса при 
не равно силе тяжести соответствующего груза.
3. 2. Теорема о движении центра масс
Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его.
Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде:
(3.5)
где N – число точек системы.
Сложим почленно уравнения между собой:
(а)
Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): 
где М – масса системы. Тогда левая часть равенства (а) запишется
(б)
Первая сумма, стоящая в правой части равенства (а), равна главному вектору 
внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется
, (3.6)
т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.
Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.
Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и L (рис. 3.4).
Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом 
, длиной R+r в точке С2. Кривошип вращается с постоянной
угловой скоростью 
. В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.
Решение. Система состоит из двух масс (N=2): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.
Запишем теорему о движении центра масс (3.6) в координатной форме
(б)
Внешними силами этой системы являются: вес станины и неподвижного диска – Mg, вес подвижного диска – mg, 
- суммарная горизонтальная реакция болтов, 
- нормальная суммарная реакция плоскости. Следовательно,
. (в)
Тогда законы движения (б) перепишутся
.
Вычислим координаты центра масс механической системы:
; (г)
как видно из (рис. 3.4), 
, 
, 
(угол поворота кривошипа 
), 
. Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от 
, 
, получим, что
(д)
Подставляя (в) и (д) в (б), находим
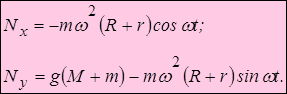
Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos
=
1 соответственно, т.е
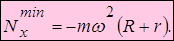
Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sin
соответственно, т.е.
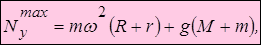
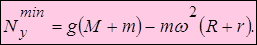
Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.
В условиях отсутствия брусков K и L (рис. 3.4), механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда 
, т.е. когда 
, отсюда следует, что угловая скорость вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству
.
3. 3. Закон сохранения движения центра масс
Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. 
, то из (3.6) следует, что ускорение центра масс 
равно нулю, следовательно, скорость центра масс 
является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.
Из этой теоремы вытекает несколько следствий.
· Одними внутренними силами нельзя изменить характер движения центра масс системы.
· Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.
· Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.
· Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).
Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.
Пример 3. Два груза массами 
и 
соединены нерастяжимой нитью, переброшенной через блок (рис. 3.5), закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.
Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести 
, 
и Mg, а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,
.
Поскольку в начальный момент система находилась в покое, имеем 
.
Вычислим координату центра масс системы при 
и в момент t1, когда груз весом g опустится на высоту H.
Для момента :
,
где 
, 
, х – соответственно координаты центра масс грузов весом g, g и клина весом Мg.
Предположим, что клин в момент времени 
переместится в положительном направлении оси Ox на величину L, если груз весом 
опустится на высоту Н. Тогда, для момента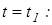 
,
т.к. грузы вместе с клином передвинутся на L вправо, a груз переместится на расстояние 
по клину вверх. Так как 
, то после вычислений получим
, откуда
.
3.4. Количество движения системы
3.4.1. Вычисление количества движения системы
Количеством движения материальной точки 
называется векторная величина, равная произведению массы точки на вектор ее скорости
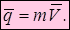
Единица измерения количества движения -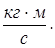 
Количеством движения механической системы 
называют векторную сумму количества движения отдельных точек системы, т.е.
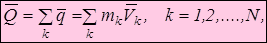
где N – число точек системы.
Количество движения механической системы можно выразить через массу системы М и скорость центра масс . Действительно,
(3.7)
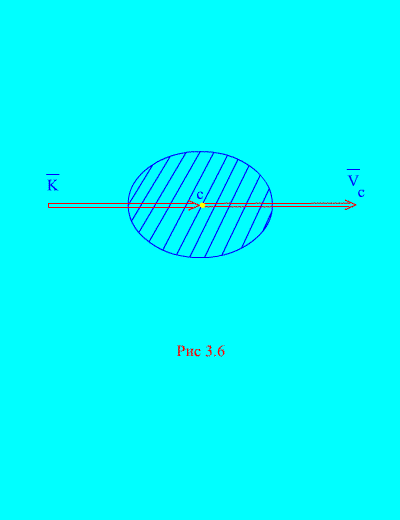
т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Направление совпадает с направлением (рис. 3.6)
В проекциях на прямоугольные оси имеем
,
где 
, 
, 
- проекции скорости центра масс системы.
Здесь М – масса механической системы; не меняется при движении системы.
Этими результатами особенно удобно пользоваться при вычислении количеств движения твердых тел.
Из формулы (3.7) видно, что если механическая система движется так, что ее центр масс остается неподвижным, то количество движения системы остается равным нулю.
3.4.2. Элементарный и полный импульс силы
Действие силы 
на материальную точку в течение времени dt можно охарактеризовать элементарным импульсом 
. Полный импульс силы за время t, или импульс силы 
, определяют по формуле
, (3.8)
или в проекциях на координаты оси
(3.8а)
Единица импульса силы - 
.
3.4.3. Теорема об изменении количества движения системы
Пусть к точкам системы приложены внешние и внутренние силы. Тогда для каждой точки системы можно применить дифференциальные законы движения (3.3), имея в виду, что 
:
.
Суммируя по всем точкам системы, получим
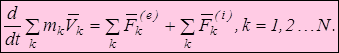
По свойству внутренних сил 
и по определению 
имеем
(3.9)
Умножая обе части этого уравнения на dt, получим теорему об изменении количества движения в дифференциальной форме:
, (3.10)
т.е. дифференциал количества движения механической системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на точки механической системы.
Вычисляя интеграл от обеих частей (3.10) по времени от 0 до t, получим теорему в конечной или интегральной форме
(3.11)
В проекциях на координатные оси будем иметь
(3.11а)
Изменение количества движения механической системы за время t, равно векторной сумме всех импульсов внешних сил, действующих на точки механической системы за то же время.
Пример 4. Груз массой m спускается вниз по наклонной плоскости из состояния покоя под действием силы F, пропорциональной времени: 
, где 
(рис. 3.7). Какую скорость приобретет тело через t секунд после начала движения, если коэффициент трения скольжения груза о наклонную плоскость равен f.
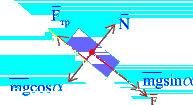
Решение. Изобразим силы, приложенные к грузу: mg – сила тяжести груза, N – нормальная реакция плоскости, 
- сила трения скольжения груза о плоскость, причем 
. Направление всех сил изображено на (рис. 3.7).
Направим ось х вдоль наклонной плоскости вниз. Запишем теорему об изменении количества движения (3.11) в проекции на ось х:
(а)
По условию 
, т.к. в начальный момент времени груз находился в состоянии покоя. Сумма проекций импульсов всех сил на ось х равна
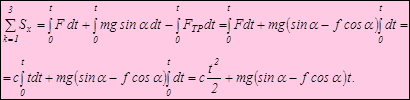
Следовательно,
,
откуда
.
3.4.4. Законы сохранения количества движения
Законы сохранения получаются как частные случаи теоремы об изменении количества движения. Возможны два частных случая.
· Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т.е. 
, то из теоремы следует (3.9), что 
,
т.е. если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению.
· Если проекция главного вектора внешних сил на какую-либо координатную ось равна нулю, например Ох, т.е. 
, то проекция количества движения на эту ось величина постоянная 
.
Рассмотрим пример применения закона сохранения количества движения.
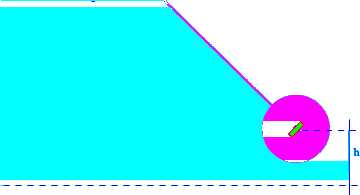
Пример 5. Баллистический маятник представляет собой тело массой , подвешенное на длинной нити (рис. 3.8).
Пуля массой , движущаяся со скоростью V и попадающая в неподвижное тело, застревает в нем, и тело отклоняется. Какова была скорость пули, если тело поднялось на высоту h ?
Решение. Пусть тело с застрявшей пулей приобрело скорость 
. Тогда, пользуясь законом сохранения количества движения при взаимодействии двух тел, можно записать 
.
Скорость можно вычислить, воспользовавшись законом сохранения механической энергии 
. Тогда 
. В результате находим
.
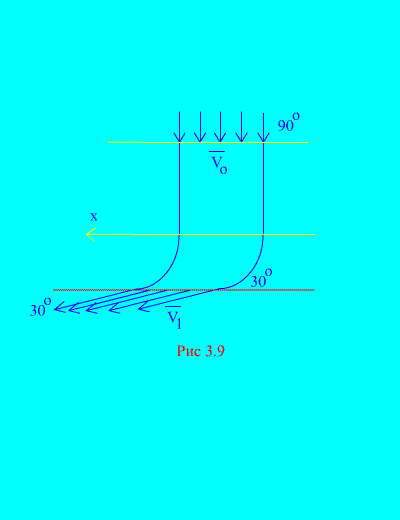
Пример 6. Вода входит в неподвижный канал (рис. 3.9) переменного сечения со скоростью 
под углом 
к горизонту; площадь поперечного сечения канала при входе 
; скорость воды у выхода из канала 
и составляет угол 
с горизонтом.
Определить горизонтальную составляющую реакции, которую вода оказывает на стенки канала. Плотность воды 
.
Решение. Будем определять горизонтальную составляющую реакции, оказываемой стенками канала на воду. Эта сила равна по модулю и противоположна по знаку искомой силе. Имеем, согласно (3.11а),
. (а)
Здесь 
.
Вычисляем массу объема жидкости, поступающей в канал за время t:
,
т.е.
(б)
Величина rАV0 называется секундной массой - масса жидкости, протекающей через любое сечение трубы в единицу времени.
Такое же количество воды покидает канал за это же время. Начальная и конечная скорости даны в условии.
Вычислим правую часть равенства (а) которая определяет сумму проекций на горизонтальную ось внешних сил, приложенных к системе (воде). Единственной горизонтальной силой является горизонтальная составляющая равнодействующей реакции стенок Rx. Эта сила при установившемся движении воды является постоянной. Поэтому
. (в)
Подставляя (б) и (в) в (а), получаем
,
Откуда
.
3.5. Кинетический момент системы
3.5.1. Главный момент количества движения системы
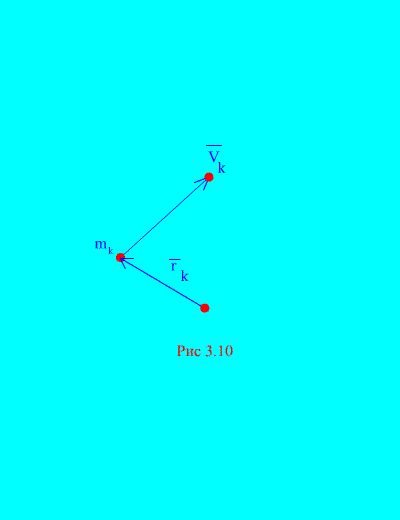
Пусть 
- радиус-вектор точки массой 
системы относительно некоторой точки А, называемой центром (рис. 3.10).
Моментом количества движения (кинетическим моментом) точки 
относительно центра А называется вектор 
, определяемый по формуле
. (3.12)
При этом вектор направлен перпендикулярно плоскости, проходящей через центр А и вектор 
.
Моментом количества движения (кинетическим моментом) точки 
относительно оси называется проекция на эту ось момента количества движения точки относительно любого выбранного на данной оси центра.
Главным моментом количества движения (кинетическим моментом) системы относительно центра А называется величина
(3.13)
Главным моментом количества движения (кинетическим моментом) системы относительно оси называется проекция на эту ось главного момента количества движения системы относительно любого выбранного на данной оси центра.
3.5.2. Кинетический момент вращающегося твердого тела относительно оси вращения
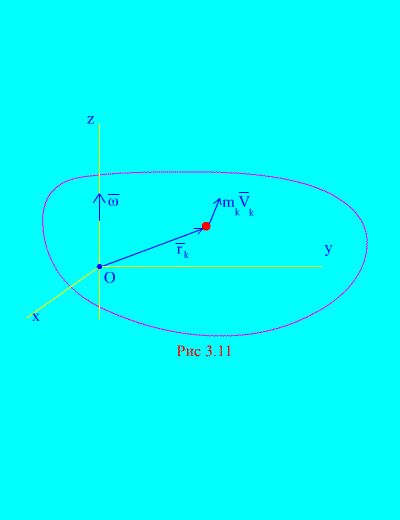
Совместим неподвижную точку О тела, лежащую на оси вращения Оz, с началом системы координат Охуz, оси которой будут вращаться вместе с телом (рис. 3.11). Пусть - радиус-вектор точки тела относительно начала координат, его проекции на оси обозначим 
, 
, 
. Проекции вектора угловой скорости тела 
на те же оси обозначим 0, 0, 
(
).
Вычислим кинетический момент тела относительно центра О. Подставим в (3.13) скорость 
точки 
: 
, получим
(3.14)
Используя формулу 
для двойного векторного произведения трех векторов 
, 
, 
, выражение 
можно переписать в виде
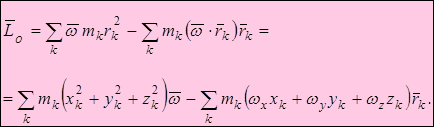
Имея в виду, что 
поскольку 
, 
; 
имеем
.
Отсюда получим следующее выражение для проекции 
вектора 
на ось Ох
.
Аналогично запишем выражения для проекций 
и 
. Учитывая формулы (2.10) и (2.12) для осевых и центробежных моментов инерции, окончательно получим
(3.15)
Если ось вращения Оz является главной центральной осью для тела, то 
и, следовательно, 
. В этом случае кинетический момент тела направлен по оси вращения Oz и равен
. (3.16)
3.5.3. Теорема об изменении кинетического момента
Пусть - скорость точки массой системы в инерциальной системе отсчета, а - ее радиус-вектор относительно начала координат (рис. 3.11). Кинетический момент системы относительно начала координат вычисляется по формуле
. (3.17)
Продифференцировав по времени обе части равенства (3.17), получим
(3.17а)
поскольку 
т.к. 
.
Если к k-ой точке системы приложить внешние и внутренние силы, то, согласно (3.3), получим
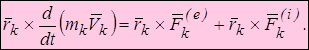
Суммируем правые и левые части последнего соотношения по всем точкам системы
(а)
Второе слагаемое полученного равенства, согласно (3.2), равно нулю. Подставляя (а) в (3.17а), получим
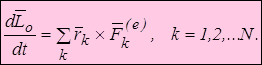
Правая часть в этом равенстве равна главному моменту 
внешних сил относительно центра О.
Таким образом,
. (3.18)
Равенство (3.18) представляет собой теорему об изменении кинетического момента относительно неподвижного центра: производная по времени от кинетического момента системы относительно неподвижного центра равна главному моменту внешних сил системы относительно этого центра.
Проецируя (3.18) на прямоугольные оси координат, получаем
(3.18,а)
Теорема об изменении кинетического момента позволяет изучать вращательное движение системы вокруг неподвижной оси.
3.5.4. Теорема об изменении кинетического момента твердого тела
Подставляя (3.15) в закон движения (3.18), получаем дифференциальные уравнения, описывающие вращение твердого тела относительно оси 0z
(3.19)
Из записанных формул видно, что если ось вращения oz является главной центральной осью, тогда 
, то (3.19) перепишутся:
. (3.20)
3.5.5. Закон сохранения кинетического момента
Если главный момент внешних сил относительно центра 
, то из (3.18) следует закон сохранения кинетического момента:
Если главный момент внешних сил относительно центра , то кинетический момент системы относительно того же центра постоянен по модулю и направлению, т.е.:
(3.21)
Если 
, 
, 
- проекции вектора 
на соответствующие оси координат, то из (3.21) следует три первых интеграла
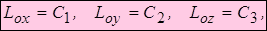
где 
- произвольные постоянные.
Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы, так же, как они не изменяют ее количество движения.
Для тела, вращающегося относительно неподвижной главной оси z, имеем
, или 
, (3.22)
где 
и 
- момент инерции тела и его угловая скорость относительно оси вращения в произвольный момент времени ; 
и 
- момент инерции тела угловая скорость в момент времени 
.
Закон сохранения кинетического момента в виде (3.22) используют в своей работе фигуристы, акробаты, танцоры.
Пример 7. Горизонтальная трубка ОА весом Mg и длиной 2а вместе с шариком, находящимся в ней на расстоянии 
от конца О и привязанным нитью к этому концу (рис. 3.12), сначала вращается по инерции вокруг вертикальной оси z, проходящей через центр О, с постоянной угловой скоростью w0, затем нить перерезают. Определить угловую скорость вращения трубки в тот момент, когда шарик вылетает из нее, если вес шарика равен mg.
Решение. Связи допускают поворот всей системы, состоящей из трубки и шарика, вокруг неподвижной вертикальной оси oz. Внешние силы Mg и mg параллельны оси вращения oz, следовательно, момент внешних сил относительно оси вращения равен нулю.
Момент инерции трубки обозначим через 
и вычислим его (рис. 3.12б). По определению 
, где dm=rdx, 
-плотность трубки. Тогда
Обратите внимание на лекцию "Реформы 1867 - 1868 гг.".
.
Момент инерции шарика относительно оси oz до отрыва нити равен ma2, а после отрыва нити в момент вылета шарика из трубки равен m(2a)2=4ma2.
Запишем закон сохранения кинетического момента (3.22)
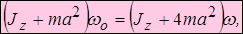
Откуда
