Геометрия масс
Лекция 2. Геометрия масс
2. 1. Центр масс
При рассмотрении движения твердых тел и механических систем важное значение имеет точка, называемая центром масс. Техника вычисления центра масс, как и моментов инерции, относится к области курсов математики; там подобные задачи служат хорошими примерами по интегральному исчислению. Напомним основные положения.
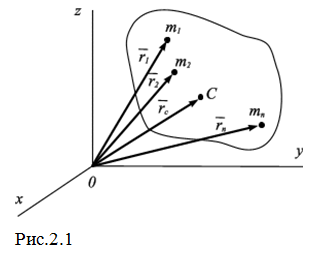
Если механическая система состоит из конечного числа материальных точек N с массами  , радиус-векторы которых проведены из одной и той же точки О –
, радиус-векторы которых проведены из одной и той же точки О –  (рис. 2.1), то центром масс называется геометрическая точка С, радиус-вектор которой
(рис. 2.1), то центром масс называется геометрическая точка С, радиус-вектор которой  определяется выражением
определяется выражением
 , (2.1)
, (2.1)
где  - масса всей системы. Обозначая декартовы координаты материальных точек
- масса всей системы. Обозначая декартовы координаты материальных точек  ,
,  …
… , из (2.1) проецированием на декартовы оси координат получим следующие формулы для координат центра масс:
, из (2.1) проецированием на декартовы оси координат получим следующие формулы для координат центра масс:
Рекомендуемые материалы
 (2.2)
(2.2)
Если механическая система представляет собой твердое тело, то формулы (2.1) и (2.2) принимают вид
 ,
,
 , (2.3)
, (2.3)
где  – масса тела. Интегрирование ведется по всему объему тела.
– масса тела. Интегрирование ведется по всему объему тела.
Для плоского тела в формулах (2.2) и (2.3)  =0, dm=rdA, A – площадь тела, интегрирование ведется по площади.
=0, dm=rdA, A – площадь тела, интегрирование ведется по площади.
2. 2. Моменты инерции твердого тела
Движение тел существенным образом зависит от характера распределения масс. Например, балерина, группируясь в танце, увеличивает или уменьшает угловую скорость своего вращения. Положение центра масс не характеризует распределение масс. Поэтому при изучении динамики механических систем точек и при изучении динамики твердого тела, вводится еще одна характеристика - момент инерции системы материальных точек и момент инерции твердого тела.
2. 3. Моменты инерции относительно точки и оси
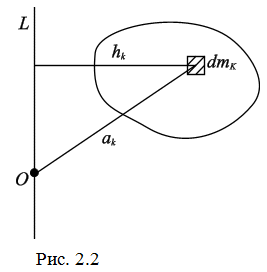
Моментом инерции системы материальных точек массой mК относительно точки О, состоящей из N точек, называется сумма произведений масс этих точек на квадраты их расстояний  до точки О (рис. 2.2), т.е.
до точки О (рис. 2.2), т.е.
 (2.4)
(2.4)
Моменты инерции относительно точки часто называют полярным моментом инерции.
Момент инерции твердого тела относительно точки О будет определятся следующим выражением:
 , (2.5)
, (2.5)
где dm – масса элементарной частицы тела, принимаемой в пределе за точку;
а – расстояние частиц тела до точки О. Интегрирование ведется по всему объему.
Моментом инерции  системы материальных точек относительно оси
системы материальных точек относительно оси  называется сумма произведений масс этих точек на квадраты их расстояний
называется сумма произведений масс этих точек на квадраты их расстояний  до оси
до оси  (рис. 2.2):
(рис. 2.2):
 (2.6)
(2.6)
В случае твердого тела сумму следует заменить интегралом:
 . (2.7)
. (2.7)
Здесь  , где
, где  – плотность тела, V – объем тела. Моменты инерции одинаковых по форме тел, изготовленных из различных материалов, отличаются друг от друга.
– плотность тела, V – объем тела. Моменты инерции одинаковых по форме тел, изготовленных из различных материалов, отличаются друг от друга.
Характеристикой, не зависящей от массы тела, является радиус инерции. Радиус инерции  относительно оси
относительно оси  определяется равенством:
определяется равенством:
 . (2.8)
. (2.8)
Тогда момент инерции относительно оси можно определить по формуле
 . (2.9)
. (2.9)
Из равенства (2.9) следует, что радиус инерции геометрически равен расстоянию от оси  той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела относительно оси
той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела относительно оси  .
.
2. 4. Моменты инерции относительно декартовых осей координат
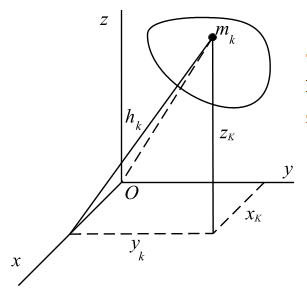
Выразим моменты инерции системы материальных точек относительно оси  (2.6) для декартовых осей координат. Расстояние k-й частицы до оси х определяется из геометрии задачи (рис. 2.3).
(2.6) для декартовых осей координат. Расстояние k-й частицы до оси х определяется из геометрии задачи (рис. 2.3).
Известно, что (теорема Пифагора)
 .
.
Аналогично
 ,
,  .
.
Подставим эти выражения в (2.6), получим моменты инерции относительно декартовых осей координат:
 (2.10,а)
(2.10,а)
Поскольку расстояние k-й частицы до центра О определяется известным выражением  , момент инерции относительно этого центра
, момент инерции относительно этого центра
 (2.10,б)
(2.10,б)
Для сплошных твердых тел формулы (2.10,а, б) примут вид
 (2.10)
(2.10)
Из формул (2.10) следует:
 . (2.11)
. (2.11)
2. 5. Центробежные моменты инерции. Главные оси инерции тела
В механике в качестве характеристик, учитывающих несимметричность в распределении масс, вводят еще так называемые центробежные моменты инерции. Если через любую точку O провести координатные оси оxyz, то по отношению к этим осям центробежными моментами инерции называют величины  , определяемые равенствами:
, определяемые равенствами:
 (2.12)
(2.12)
где  – массы точек;
– массы точек;  – координаты точек. Очевидно, что
– координаты точек. Очевидно, что  и т.д. Для твердых тел формулы (2.12) принимают вид
и т.д. Для твердых тел формулы (2.12) принимают вид

 (2.12а)
(2.12а)

В отличие от осевых центробежные моменты инерции могут быть как положительными, так и отрицательными величинами и, в частности, при определенном выборе осей могут обращаться
в нули.
Рассмотрим однородное тело, имеющее ось симметрии. Проведем координатные оси oxyz так, чтобы ось оz была направлена вдоль оси симметрии (рис. 2.4). В силу симметрии каждой точке тела с массой  и координатами
и координатами  будет соответствовать точка с другим индексом, но с такой же массой и с координатами, равными
будет соответствовать точка с другим индексом, но с такой же массой и с координатами, равными  . В результате получим, что
. В результате получим, что  (слагаемые попарно одинаковы по модулю и противоположны по знаку); отсюда, учитывая (2.12), находим, что
(слагаемые попарно одинаковы по модулю и противоположны по знаку); отсюда, учитывая (2.12), находим, что

Ось 0z, для которой центробежные моменты инерции равны нулю, называется главной осью инерции тела.
Если тело имеет ось симметрии, то эта ось является главной осью инерции твердого тела.
2. 6. Моменты инерции относительно параллельных осей.
Теорема Гюйгенса-Штейнера
Существует простая связь между моментами инерции тела относительно параллельных осей (теорема Гюйгенса-Штейнера), одна из которых проходит через центр масс.
Теорема. Момент инерции тела  относительно некоторой оси
относительно некоторой оси  равен сумме момента инерции
равен сумме момента инерции  тела относительно оси
тела относительно оси  , проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями:
, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями:
 , (2.13)
, (2.13)
где М – масса тела, d – расстояние между двумя параллельными осями.
Пусть оси  и
и  параллельны, причем ось
параллельны, причем ось  проходит через точку С – центр масс тела.
проходит через точку С – центр масс тела.
Возьмем начало координат в точке С, совместим ось z с осью  , а ось у направим так, чтобы она пересекала оси
, а ось у направим так, чтобы она пересекала оси  и
и  (рис. 2.5).
(рис. 2.5).
Выделим в теле произвольный элемент массой dm и опустим из него перпендикуляры на оси z и  , обозначив их соответственно h и
, обозначив их соответственно h и  . Согласно определению осевых моментов инерции моментов (2.7), будем иметь
. Согласно определению осевых моментов инерции моментов (2.7), будем иметь
 .
.
По теореме косинусов (рис.2.5) найдем  , однако
, однако  , где у – координата элемента, тогда
, где у – координата элемента, тогда
 .
.
Подставим полученное выражение  в формулу (2.13), определяющую момент инерции
в формулу (2.13), определяющую момент инерции  :
:
 .
.

Первый интеграл равен  по определению, второй – массе тела М, а третий – нулю:
по определению, второй – массе тела М, а третий – нулю:  , поскольку начало координат совпадает с центром масс. Следовательно,
, поскольку начало координат совпадает с центром масс. Следовательно,
 .
.
Эта формула широко используется в практических расчетах при определении моментов инерции тел относительно осей, не проходящих через центр масс. Применяя метод разбиения, с помощью этой формулы можно определять осевые моменты инерции тел сложной формы.
Установим формулы для центробежных моментов инерции, аналогичные (2.13). Рассмотрим две системы координат с взаимно параллельными осями  и Сxyz, где С-центр масс тела (рис. 2.6). Обозначим через a,b,c координаты точки С в системе
и Сxyz, где С-центр масс тела (рис. 2.6). Обозначим через a,b,c координаты точки С в системе  Тогда формулы перехода от одной системы координат к другой будут иметь вид
Тогда формулы перехода от одной системы координат к другой будут иметь вид
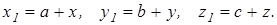
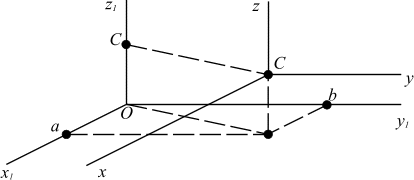
Рис. 2.6
По определению центробежных моментов инерции имеем
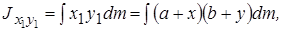
или, раскрывая скобки, группируя члены и вынося постоянные множители за знак интеграла,

Первый интеграл равен массе тела М, второй и третий равны нулю (они соответственно определяют положение центров тяжести  ), а последний равен
), а последний равен  по определению. Таким образом, имеем (две другие формулы получены аналогично)
по определению. Таким образом, имеем (две другие формулы получены аналогично)
 (2.14)
(2.14)
2. 7. Моменты инерции простейших однородных тел
Получим формулы для вычисления моментов инерции некоторых простых тел.
Однородный стержень
Имеем однородный стержень длиной L и массой М. Вычислим момент
инерции стержня относительно оси Сz, проходящей через центр масс стержня и перпендикулярной к нему (рис. 2.7).

Для этого нужно просуммировать все массы, умноженные на квадраты расстояния x до оси Cz. Тогда, согласно(2.7), имеем
 .
.
Если разделить стержень на отрезки длиной dx, то соответствующий элемент массы будет пропорционален dx (dm~dx), а если бы dx составляло длину всего стержня, то его масса была бы равна М (M~L). Поэтому

Вычисляя интеграл, получаем
 .
.
Таким образом,
 . (2.15)
. (2.15)
Размерность момента инерции всегда равна массе, умноженной на квадрат длины (кг м2), так что единственная величина, которую мы вычислили, это множитель  .
.
Момент инерции стержня относительно оси  , проходящей перпендикулярно стержню через его конец, параллельно zС, определяется по теореме Гюйгенса-Штейнера:
, проходящей перпендикулярно стержню через его конец, параллельно zС, определяется по теореме Гюйгенса-Штейнера:
 , где
, где  .
.
Следовательно,  .
.
Прямоугольная пластина
Тонкая прямоугольная пластина имеет размеры L и H и массу М. Оси Ох и Оу расположены в плоскости пластины (рис. 2.8), тогда для всех точек  . Формулы для вычисления
. Формулы для вычисления  и
и  (2.10) принимают вид
(2.10) принимают вид
 . (2.16)
. (2.16)

Для вычисления  разобьем пластину на элементарные полосы шириной dy и массой
разобьем пластину на элементарные полосы шириной dy и массой  и проинтегрируем по у от 0 до H:
и проинтегрируем по у от 0 до H:
 ,
,
здесь  .
.
Момент инерции  вычислим по аналогии:
вычислим по аналогии:
 .
.
Для определения момента инерции пластины относительно оси Оz, воспользуемся формулой (2.10)

Здесь A - площадь прямоугольной пластины.
Итак, для моментов инерции пластины относительно осей координат получены формулы
 (2.17)
(2.17)
Упомянем свойство, которое полезно при нахождении моментов инерции плоских тел. Оно состоит в следующем. Если есть плоская фигура и оси координат x и y расположены на этой плоскости, а ось z направлена перпендикулярно к ней, то моменты инерции этой фигуры равны


Доказать это просто, поскольку все  =0.
=0.
Круглый диск
Имеем тонкий однородный диск радиусом R и массой М (рис. 2.9, а). Вычислим момент его инерции  относительно точки О. Этот момент инерции совпадает с моментом инерции
относительно точки О. Этот момент инерции совпадает с моментом инерции  относительно координатной оси Оz, перпендикулярной плоскости диска (рис. 2.9, a). Действительно, согласно (2.10),
относительно координатной оси Оz, перпендикулярной плоскости диска (рис. 2.9, a). Действительно, согласно (2.10),

поскольку  , следовательно,
, следовательно,  .
.
Разобьем диск на концентрические полосы шириной dr (рис. 2.9, б). За элемент массы dm возьмем массу кольца толщиной dr. Такой выбор элемента массы объясняется тем, что расстояния от всех точек до центра диска одинаковы и равны r (радиальная симметрия). Элемент массы dm равен ее площади  , умноженной на плотность
, умноженной на плотность  (А - площадь диска).
(А - площадь диска).

Тогда 
Для всего диска
 .
.
Таким образом,
 . (2.18)
. (2.18)
Для осей Ох и Оу, расположенных в плоскости диска, в силу симметрии  . Используя формулу (2.11), имеем
. Используя формулу (2.11), имеем  , но
, но  , поэтому J0 =2Jx , тогда Jx=Jy=
, поэтому J0 =2Jx , тогда Jx=Jy= J0 , т.е.
J0 , т.е.
 . (2.19)
. (2.19)
Момент инерции цилиндра относительно его осей
Пусть радиус цилиндра равен R, а его масса М, высота Н. Построим цилиндрическую трубку радиуса r  высотой Н толщиной dr и
высотой Н толщиной dr и
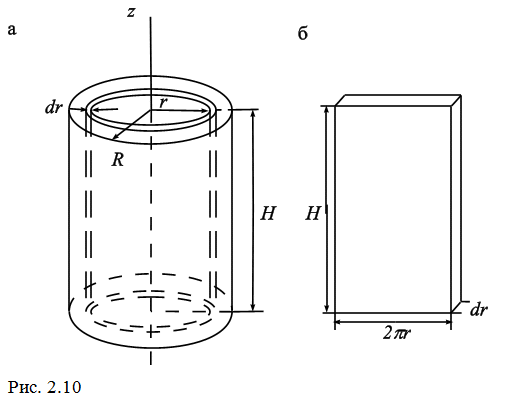
За элемент массы dm возьмем массу этой трубки. Объем трубки равен  (рис. 2.10, б), а ее масса
(рис. 2.10, б), а ее масса  ,
,  - плотность. Объем всего цилиндра
- плотность. Объем всего цилиндра  . Следовательно,
. Следовательно,
 .
.
Тогда
 . (2.20)
. (2.20)
Пример. Физический маятник, изображенный на рис. 2.11, состоит из тонкого однородного стержня длиной L и массой  и круглого однородного диска радиусом R и массой
и круглого однородного диска радиусом R и массой  . Определить момент инерции
. Определить момент инерции  маятника, относительно оси его вращения Оz (ось Оz направлена перпендикулярно к плоскости рисунка).
маятника, относительно оси его вращения Оz (ось Оz направлена перпендикулярно к плоскости рисунка).

Решение. Маятник состоит из двух тел: стержня (1) и диска (2).
Поэтому
 ,
,
где  и
и  - моменты инерции относительно оси Оz соответствующих тел.
- моменты инерции относительно оси Оz соответствующих тел.
Момент инерции стержня
 ,
,
а момент инерции диска найдем по формуле (2.12):
 .
.
Здесь JZC - момент инерции диска относительно оси, проходящей через центр C, параллельной оси Оz, а  - расстояние от центра диска до оси Оz.
- расстояние от центра диска до оси Оz.
Вычислим момент инерции маятника:
 .
.
Перечислим свойства момента инерции плоской фигуры относительно оси z, направленной перпендикулярно к плоскости фигуры (плоскости xoy).
· Момент инерции равен
 ,
,
где r - плотность; А - площадь плоской фигуры.
· Если тело состоит из нескольких частей, причем момент инерции каждой составной части известен относительно одной оси z, то полный момент инерции равен сумме моментов инерции этих частей:
 .
.
· равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс:
 .
.
· Момент инерции плоской фигуры относительно оси, перпендикулярной к плоской фигуры, равен сумме моментов инерции относительно любых двух других взаимно перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с перпендикулярной осью:

Обычно моменты инерции твердых тел вычисляются интегрированием сравнительно легко только в том случае, когда эти тела однородные и имеют правильную геометрическую форму. В случае же неоднородных тел и тел, имеющих сложные очертания, моменты инерции надежнее и проще определять экспериментально с помощью соответствующих приборов. Один из таких методов рассмотрен в лекции 3.
Моменты инерции некоторых элементарных фигур, имеющих постоянную плотность ρ, см. в таблице.
Таблица
| Фигура | Ось z | ρ |
|
| Тонкий стержень длиной L (рис.2.7) | Проходит через центр С, перпендикулярно стержню |
|
|
| Прямоугольник со сторонами L и H (рис.2.8) | Проходит через центр параллельно стороне H |
|
|
| Прямоугольник со сторонами L и H (рис.2.8) | Проходит через центр, перпендикулярно к плоскости |
|
|
| Диск радиуса R (рис.2.9) | Проходит через центр, перпендикулярно плоскости |
|
|
| Круговой цилиндр радиусом R, длиной H (рис.2.10) | Проходит через центр параллельно H | "6.7. Стереоскопические способы" - тут тоже много полезного для Вас.
|
|
| Круговой цилиндр радиусом R, длиной H (рис.2.10) | Проходит через центр перпендикулярно H |
|
|


 .
.
 .
.
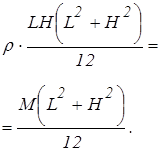

 .
.
 .
.



















