Динамика материальной точки

Лекция 1. Динамика материальной точки.

1. 1. Основные понятия

Классическая механика создана в XVII в. Галилео Галилеем (1564–1642), Рене Декартом (1596–1656), Христианом Гюйгенсом (1629–1695) и другими учеными XVII века. В  конечной форме классическая механика  сформулирована Исааком Ньютоном (1642–1727). Ньютон изложил основы классической механики в более строгой, систематической и законченной форме, чем его предшественники, поэтому классическую механику называют «механикой Ньютона».

В динамике изучаются механические движения (т. е. перемещения) материальных объектов под действием сил.

Сила считается в механике основным понятием. Силы не являются в механике какими-либо самостоятельными сущностями, независимыми от материальных тел. Они создаются материальными телами и полями. Поэтому можно сказать, что посредством сил материальные тела действуют друг на друга, т.е. взаимодействуют. Сила при этом выступает как векторная количественная мера интенсивности взаимодействий. Силы не только изменяют скорость движения материальных тел, но и вызывают их деформации. Наиболее простым и наглядным примером деформированного тела является сжатая или растянутая пружина.

Движение материальных объектов всегда следует рассматривать относительно определенной системы отсчета. Оно совершается в пространстве с течением времени. В классической механике, в основу которой положены аксиомы Ньютона, пространство считается однородным, изотропным трехмерным евклидовым пространством. Если тело не меняет своей формы и размеров при параллельном переносе, – значит пространство однородно, в нем нет выделенных точек. Если тело не меняет формы и размеров при вращении, значит пространство изотропно, в нем нет выделенных направлений. Движение в однородном изотропном пространстве не меняет формы и размеров тела – оно меняет лишь его положение относительно системы отсчета.

В евклидовом пространстве координаты подчиняются евклидовой геометрии, т. е. геометрии, основанной на системе аксиом, постулатов и теорем, сформулированных Эвклидом в III веке до н.э. Основой эвклидовой геометрии является постулат о "параллельных" прямых. Согласно этому постулату, через точку, взятую вне прямой, можно провести только одну прямую, не пересекающуюся с данной. Из этого постулата вытекает, что сумма углов треугольника равна двум прямым углам и ряд других утверждений.

Рекомендуемые материалы

Николай Лобачевский (1793–1856) в 1826 г. предположил, что может существовать другая геометрия, в которой допускается существование бесчисленного множества прямых, не пересекающих данную и проходящих через взятую вне ее точку. В геометрии  Лобачевского сумма углов треугольника меньше двух прямых углов.

Бернхард Риман (1826–1186) в 1854г. сформулировал другую неэвклидову геометрию, в которой через точку, взятую вне прямой, нельзя провести ни одной прямой, не пересекающей данную; иными словами, любые две параллельные линии обязательно пересекутся. Геометрия Римана отказывает параллельным линиям в существовании. В этой геометрии сумма углов треугольника больше двух прямых углов; различные перпендикуляры к прямой не параллельны (как в эвклидовой геометрии), и не расходятся (как в геометрии Лобачевского), а пересекаются.

Основные законы движения

Инерциальная система отсчета

Начиная с Аристотеля (384–322 г. до н. э.) считалось, что движение тела всегда поддерживается некоторой действующей причиной и, как правило, только эта причина иссякает, тело немедленно останавливается. Только в XVII в. появилась и победила концепция движения, согласно которой движение по инерции, т. е. прямолинейное и равномерное движение тела, представляет собой неизменное состояние и не требует какой-либо поддерживающей силы. Тело, предоставленное самому себе, сохраняет неизменное состояние покоя или равномерного и прямолинейного движения, иными словами, сохраняет постоянную скорость – нулевую или конечную. Сформулировал принцип инерции итальянский ученый Галилео Галилей.

В различных системах отсчета математическая форма законов природы различна, однако существуют так называемые инерциальные системы отсчета, в которых эти законы имеют наиболее простой вид.

Инерциальной системой называются система отсчета, в которой  материальная точка при отсутствии действующих на нее сил взаимодействия, движется прямолинейно и равномерно, т.е. системы, для которой справедлив принцип инерции Галилея.

Принцип инерции Галилея устанавливает, что всякое тело пребывает в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока внешние силы не выведут его из этого состояния, т.е. состояния покоя и состояния прямолинейного и равномерного движения неразличимы. С достаточной точностью такой инерциальной системой можно считать гелиоцентрическую систему координат. В большинстве технических задач инерциальная система отсчета может быть связана с Землей.

Механика Ньютона пользуется некоторыми приближенными представлениями. К ним принадлежат представления о материальной точке, механической системе, абсолютно твердом теле.

Чтобы определить положение тела в пространстве одним числом на линии, двумя – на поверхности, тремя – в трехмерном пространстве, нужно рассматривать это тело как точку, т. е. игнорировать его размеры. Считая тела материальными точками, можно говорить о расстоянии между телами как об одной величине.

Объектом изучения в динамике являются:

· материальная точка – тело конечной массы, положение и движение которого в пространстве можно определять как для объекта, не имеющего размеров, т.е. геометрической точкой. Это условие выполнено, если при изучении движения можно пренебречь размерами тела и его вращением. Можно или нельзя принять материальное тело за материальную точку, зависит от конкретной задачи;

· механическая система (или просто система) – выделенная каким - либо образом совокупность материальных точек;

· абсолютно твердое тело (или просто тело) – механическая система, расстояние между точками которой  не меняется. Абсолютно твердое тело является моделью материального тела.

Механика рассматривает сначала движение отдельной материальной точки, а затем переходит к системам материальных точек – абсолютно твердым телам, и к механическим системам, состоящим из конечного числа отдельных материальных точек, связанных между собой определенными взаимодействиями.

Чтобы ответить на вопрос,  как изменяется скорость тела, если на него действует сила, Исаак Ньютон сформулировал три закона.

1. 2. 1.    Первый закон Ньютона

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние.

Под телом здесь подразумевается материальная точка. Сила определяется как причина, изменяющая равномерное и прямолинейное движение материальной точки. За меру силы Ньютон принял то ускорение, которое эта сила вызывает. Поэтому в механике эта сила называется ускоряющей. Первый закон Ньютона еще называют законом инерции. Под инерцией понимают способность тела сохранять свое движение или состояние покоя при отсутствии сил или изменять это состояние под действием силы.

1. 2. 2. Второй закон Ньютона

Количеством движения материальной точки называется векторная величина , равная произведению массы точки на вектор ее скорости –  .

Изменение количества движения пропорционально приложенной силе, направление вектора изменения количества движения совпадает с линией действия этой силы.

Математически этот закон записывается в виде векторного уравнения

                                                    (1.1)

где m – масса движущейся точки; – скорость движущейся точки;  –  сила. Считая массу материальной точки величиной постоянной, второй закон Ньютона можно представить в виде формулы:

,                                                          (1.2)

т.е. ускорение , которое получает материальная точка, пропорционально действующей на точку силе. В таком виде в 1736г. основной закон записан Леонардом Эйлером (1707–1783).

Масса m входит в это уравнение, как коэффициент пропорциональности между силой и ускорением. Масса является характеристикой инертного свойства материальной точки, т.е. способности ее под действием заданной силы получать определенное ускорение. Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе – главному вектору , равному геометрической сумме этих сил. Тогда закон (1.2) примет вид

                                              (1.2а)

Этот же результат можно получить, используя вместо аксиомы параллелограмма аксиому независимого действия сил.

Аксиома. При одновременном действии на материальную точку нескольких сил ускорение точки, относительно инерциальной системы отсчета, от действия каждой отдельной силы, не зависит от наличия других приложенных к точке сил и  равно векторной сумме ускорений от действия отдельных сил.

Второй закон (основной закон динамики) остается справедливым и для несвободной материальной точки, на которую наложены связи. Следует только отбросить связи, заменить их реакциями связи и  в число приложенных внешних сил включить силы реакций связей.

1. 2. 3. Третий закон Ньютона

Действию всегда есть равное противодействие, другими словами – действия двух материальных точек друг на друга всегда равны по модулю, направлены в противоположные стороны вдоль прямой, соединяющей эти точки (линии действия).

Законы (аксиомы) классической механики хорошо согласуются с результатами опытов для скоростей, много меньших скорости света в пустоте (V<<C, С – скорость света). Для скоростей порядка скорости  света  (VC), следует применять механику специальной теории относительности. Размеры тела должны быть много больше межатомного расстояния в твердом теле, т.е. >>, здесь . Для тел, размеры которого  L ~, следует применять квантовую механику.

Системы единиц. Для измерения всех механических величин достаточно ввести три основные единицы измерения: единицу длины, единицу времени и единицу измерения массы или силы. В международной системе единиц измерения физических величин (CИ), основными являются метр (м), секунда (с), килограмм массы (кг). Единицей измерения силы является производная единица - 1 Ньютон (Н); 1Н – это сила, сообщающая массе в 1 кг ускорение 1(1Н=1).

1. 3. Две основные задачи динамики точки

В динамике точки рассматривают две основные задачи.

Первая задача: В некоторой системе отсчета заданы уравнения движения материальной точки массой m. Требуется определить силу или силы, под действием которых происходит это движение.

Вторая задача: На материальную точку массой m действует сила, определенная в каждой точке пространства; требуется определить уравнение движения материальной точки, происходящее под действием этой силы.

1. 3. 1. Первая задача динамики

Зная массу точки и ее уравнение движения, можно найти действующую на точку силу.

А. Уравнения движения точки в декартовых координатах

Действительно, если заданы уравнения движения точки в декартовой системе координат

,

то проекции силы на оси координат определяются из уравнений (1.2)

                      (1.3)

Зная проекции силы на координатные оси, легко определить модуль силы и направляющие косинусы углов силы с осями координат.

Пример 1. Груз спускается вниз по шероховатой  наклонной плоскости, расположенной под углом  к горизонту, двигаясь согласно уравнению . Определить модуль силы трения скольжения груза о плоскость.

Решение. Совместим ось x c направлением движения тела. К грузу приложены три силы: сила трения , реакция поверхности  и вес тела(рис. 1.1).

Составим дифференциальное уравнение движения груза в проекции на ось х:

.                             (а)

Так как , то , уравнение (а) примет вид

,

откуда

.

Следует отметить, что решение накладывает ограничения на условия задачи и справедливо только, когда

Пример 2. Материальная точка массы m движется согласно уравнениям , . Определить силу , вызывающую это движение, если известно, что сила зависит только от положения точки, т.е. .

Решение. Уравнение траектории движения, согласно заданным уравнениям движения: , т. е. точка вращается по окружности против часовой стрелки (рис. 1.2). Совместим систему координат с центром окружности и составим уравнение (1.3) в проекциях на оси получим:

Модуль силы

,

где r – модуль радиус-вектора материальной точки  (рис. 1.2).

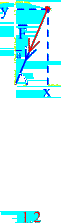
Направление силы  определяем по направляющим косинусам:

.

.

Так как величины  и  определяют углы, образуемые соответственно осями х и у с радиус-вектором  ,  то сила  направлена от точке М к центру окружности  (рис. 1.2). Такая сила называется центральной.

Б. Естественные уравнения движения

Если точка движется по известной траектории, радиус кривизны которой известен, то следует использовать в качестве системы координат   оси естественного трехгранника (трехгранник Френе). Такие оси, как известно из кинематики, называются естественными осями координат . Проекции ускорения точки на естественные оси имеют вид

.

Обозначая проекции сил на естественные оси  через , , , получим закон движения материальной точки в проекциях на эти оси

                   (1.4)

Из этих уравнений видно, что  > 0 и = 0. Таким образом, сила, действующая на материальную точку, всегда расположена в соприкасающейся плоскости к траектории движения точки и направлена в сторону вогнутости траектории.

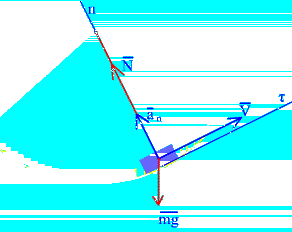
 Пример 3. Вездеход массой  2000 кг движется по оврагу с постоянной скоростью . Определить давление вездехода на дно оврага, когда радиус кривизны . Силой сопротивления движению пренебречь.

Решение. Примем вездеход за материальную точку, тогда на нее действуют две силы:  вес  и  реакция грунта(рис. 1.3). Направим ось  по горизонтали в сторону движения, а ось n по вертикали вверх.

 Составим  уравнения (1.4), учитывая, что  поскольку .

Закон движения точки примет вид

,

.

Откуда

Здесь учтено, что

.

Отметим, что давление вездехода на дно оврага больше его веса . Следовательно, чтобы уменьшить давление на грунт, необходимо снизить скорость.

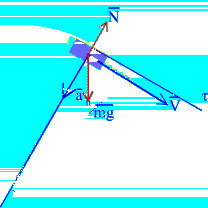
Если вездеход будет двигаться по холму (рис. 1.4), то направление нормальной составляющей ускорения  будет совпадать с направлением веса вездехода .

Тогда

,

.

В этом случае давление вездехода на грунт будет меньше веса. Следовательно, для уменьшения давления на грунт нужно увеличить скорость.

Из примеров видно, что первая задача динамики сводится к чисто кинематическим расчетам.

1. 3. 2. Вторая задача динамики

По заданной массе и действующей на точку силе можно определить уравнения движения этой точки.

Рассмотрим решение этой задачи в декартовой системе координат. В общем случае сила  является функцией многих переменных. Проецируя (1.2) на декартовы оси, получим

                                (1.5)

если рассматривать случай зависимости силы только времени, координат и скорости.

Законы движения материальной точки представляют собой систему трех линейных дифференциальных уравнений второго порядка относительно неизвестных функций  х(t), у(t), z(t), где независимым параметром  является время t.

Общий интеграл этих уравнений содержит шесть произвольных постоянных. Функции, удовлетворяющие дифференциальным уравнениям движения точки и содержащие шесть произвольных  постоянных интегрирования, называются общим решением дифференциальных уравнений  движения свободной точки и записываются в виде

В каждой конкретной задаче постоянные интегрирования определяются из начальных условий задачи:

                (1.6)

где , , - координаты движущейся точки; , ,  - проекции ее скоростей (рис. 1.5).

Подчинив найденные первые и вторые интегралы дифференциальных уравнений (1.5) начальным условиям задачи (1.6), вычисляют все шесть постоянных интегрирования. Начальные условия задачи определяют единственное решение системы дифференциальных  уравнений.

Интегрировать уравнения движения (1.5) можно с помощью определенных интегралов. Тогда нижние пределы интегрирования будут соответствовать значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, верхние пределы интегрирования будут соответствовать значению интегрируемых величин при текущем времени t.

1. 3. 3. Основные виды прямолинейного движения точки

При прямолинейном движении скорость и ускорение точки все время направлены вдоль траектории точки. Совместим ось Ox с траекторией движущейся точки,  тогда дифференциальное уравнение прямолинейного движения точки, согласно (1.5), имеет вид 

                                            (1.5а)

Начальные условия задачи задают в виде:

при .

Наиболее простыми и интересными примерами прямолинейного движения материальной точки являются примеры, когда сила зависит от одного параметра.

Рассмотрим конкретные примеры на составление и интегрирование дифференциального уравнения (1.5а). Эти примеры позволят выявить некоторые особенности в решениях таких задач.

1. Постоянная сила

 

Пример 4. В результате полученного толчка тело весом mg начало скользить вниз с начальной скоростью  по шероховатой поверхности, расположенной под углом  к горизонту (рис. 1.6). Определить путь, пройденный телом за время , если коэффициент трения скольжения тела по поверхности равен .

Решение. Направим ось х вдоль наклонной поверхности (рис. 1.6). Совместим начало отсчета на оси х с положением тела в начальный момент времени.

Начальная скорость  направлена вдоль оси х вниз, следовательно, начальные условия задачи имеют вид

.

Тело не является свободным. Мысленно отбросим наклонную поверхность и заменим ее действие на тело реакцией . Реакция шероховатой поверхности  имеет две составляющие: нормальную  и силу трения  (и направлена перпендикулярно поверхности, сила  направлена в сторону, противоположную предполагаемому движению).

Запишем закон движения (1.5а):

и после сокращения на m , получим

.                                       (а)

Согласно определению ускорения  = , тогда (а) запишем как

.                                    (б)

Получили линейное дифференциальное уравнение с неразделенными переменными. Для разделения  переменных помножим правую и левую части уравнения  (б) на dt,

.

Проинтегрируем  правую и левую части последнего уравнения с учетом заданных начальных условий (). Нижние пределы интегрирования правой и левой части уравнения соответствуют значениям интегрируемых величин при  t = 0, верхние пределы интегрирования  – соответствуют значениям интегрируемых величин при текущем времени t,  т.е.

.

Вычислим интегралы

.

Для определения уравнения движения тела используем подстановку , получим

.

Разделяя переменные

.

Проинтегрируем полученное уравнение с учетом заданных начальных условий (t = 0, x = 0):

.

Вычисляя, получим

.

Подставив заданное значение   и = 4, получим путь, пройденный телом за 2с:

2. Сила зависит от координаты (например, силы упругости)

Пример 5. Груз весом mg прикреплен к правому концу пружины, левый конец которой закреплен в стене (рис. 1.7). В начальный момент времени груз оттянули вдоль гладкой поверхности на величину  и отпустили. Найти уравнение движения груза, если сила упругости пружины равна .

 Решение. Запишем начальные условия задачи:

.                            (а)

Составим дифференциальный закон движения (1.5а):

или

.                                                       (б)

Для разделения переменных в (б), скорость нужно определить как функцию от координат,  т.е. .

Тогда

.                             (в)

Подстановка (в) позволит исключить из дифференциального уравнения (б) время:

.

Разделим переменные: умножим обе части этого уравнения на dx:

.

Вычисляя интегралы от обеих частей уравнения с учетом начальных условий (а), получим

.

Вычислим интегралы

.

Находим

.                                            (г)

Для определения уравнения движения тела используем подстановку , получим

.

Разделим переменные: умножим на dt и поделим на  правую и левую части и затем проинтегрируем полученное уравнение с учетом начальных условий (а):

.

Вычислим правый и левый интегралы:

или

.                        (д)

Известно, что , тогда уравнение движения (д) примет вид

Из полученного уравнения видно, что тело будет совершать гармонические колебания с амплитудой  (рис. 1.7).

3. Сила зависит от времени

Пример 6. Груз весом  начинает двигаться прямолинейно из состояния покоя вдоль гладкой горизонтальной поверхности под действием силы , направленной вдоль оси ox. Вычислим  уравнение движения груза.

Решение. Выберем начало отсчета О в начальном положении груза и направим ось oх в сторону предполагаемого движения (рис. 1.8).

Начальные условия задачи имеют вид:

при , ,.

Составим  закон движения груза (1.5а):

.

Разделим переменные по известной схеме и проинтегрируем полученное уравнение с учетом начальных условий задачи

,

откуда

.                                                     (а)    

Для определения уравнения движения тела используем подстановку , получим

.

Разделим переменные (помножим правую и левую части уравнения наи проинтегрируем полученное уравнение с учетом начальных условий

.

Вычисляя интегралы в правой и левой части уравнения, получим уравнение движения груза

.

4. Сила зависит от скорости

Пример 7. Точка массой m падает вертикально вниз без начальной скорости под действием силы тяжести, испытывая силу сопротивления воздуха , где k – положительная константа, которая зависит от плотности среды и площади проекции тела на плоскость, перпендикулярную направлению движения (рис. 1.9). Найти уравнение движения точки.

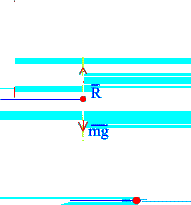
Решение. Направим ось х вертикально вниз, выбрав за начало координат положение точки в нулевой момент времени, т.е.  (рис. 1.9). В произвольный момент времени прикладываем к точке действующие на нее силы  и . Составим дифференциальный закон движения (1.5а)    

.

Сократив на m правую и левую части уравнения и заменим  на , получим 

.                                          (а)        

Разделим переменные, помножим на dt и разделим на  правую и левую части (а). Проинтегрируем полученное выражение с учетом начальных условий:

.

Вычисляя интегралы, получим

,

откуда  

 

 или 

  ,                                    (б)

поскольку  lg1=0.

Потенцируя уравнение (б) и далее решая относительно V, имеем

,

 откуда  

.                                        (в)

Переходя к пределу при , получим предельную скорость падения тела:

.

Предельную скорость можно получить проще из условия максимума скорости, т.е. равенства нулю ускорения (а):

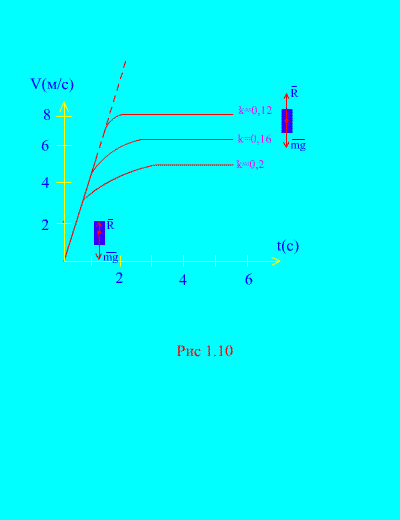
Скорость, близкая к предельной, устанавливается довольно быстро (рис. 1.10). Величина скорости зависит от значения константы k. Если не учитывать  сопротивление среды (k=0), то предельного значения скорости нет:  пунктирная кривая на (рис. 1.10); при увеличении константы k , предельная скорость уменьшается.

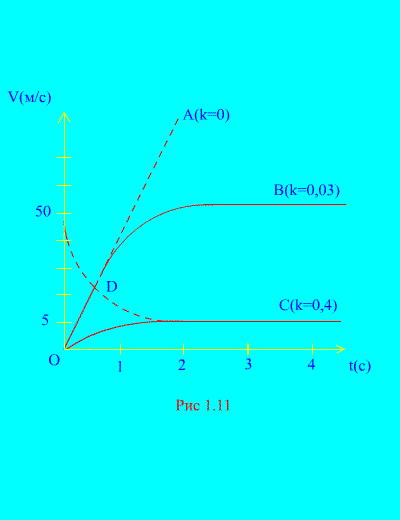
На (рис. 1.11) показано  падение тела массой  с высоты без парашюта (k0,003) ­­–  кривая В и с парашютом (k0,4)  – кривая С. Если начальная скорость падения тела не нулевая (например ), то при падении тела с парашютом (k0,4), скорость быстро затухает до своего критического значения – пунктирная кривая кривая D на (рис. 1.11).

Продолжим вычисление уравнения движения падающей точки. Заметим, что правую часть выражения (в) можно представить через гиперболический тангенс (th х):

.

Тогда выражение (в) можно записать как

.

Подставим вместо V ее значение , разделяя переменные и интегрируя правую и левую части, получим

,

или

.

Итак, уравнение движения падающей точки имеет вид

.

Здесь ch х – гиперболический косинус.

Замечание. При вычислении интегралов полезно пользоваться таблицей интегралов.

1. 4. Криволинейное движение точки

Одним из наиболее важных приложений законов движения свободной материальной точки является задача о движении точки под действием силы тяжести в плоскости. Рассмотрим движение материальной точки, на которую действует сила тяжести с учетом и без учета сопротивления среды.

1. 4.1. Движение материальной точки в пустоте

Рассмотрим движение материальной точки, на которую действует только сила тяжести (сила, имеющая постоянную величину и направление).

Выберем неподвижную систему координат так, чтобы ее начало совпадало с начальным положением точки, а ось y направим вертикально вверх. Ось x расположим в плоскости движения (рис. 1.12)

Начальная скорость точки  образует угол  с осью x. Тогда начальные условия задачи запишутся

            (1.7)

Составим дифференциальные уравнения движения точки в проекциях на оси координат. На точку действует сила тяжести, направленная по вертикали вниз. Тогда дифференциальные уравнения движения точки в плоскости имеют  вид

          (1.8)

Интегрируя первое уравнение  (1.8) с учетом начальных условий  (1.7), имеем

Интегрируя второе уравнение (1.8) с учетом начальных условий  (1.7), имеем

Интегрируя третье уравнение (1.8) с учетом начальных условий  (1.7) имеем

Из полученных уравнений видно, что точка движется в соприкасающейся плоскости xoy, согласно уравнениям движения

  

.          (1.9)

Проведем исследования уравнений движения точки (1.9). Исключим из них  параметр t (время), получим уравнение траектории движения в явном виде

,                                    (1.10)

которое представляет собой уравнение параболы. Вершина параболы может быть определена из условия

,

т.е.                        

,

откуда

.                                   (1.11)

Дальность полета по горизонтали ОА (рис. 1.11), за счет симметричности траектории, равна

 .       (1.12)

Из выражения (1.12) видно, что

· при углах  и  тело падает в одну и ту же точку, т.к. ;

· максимальная дальность полета обеспечивается при , т.е. при , тогда максимальная дальность полета ОС (рис. 1.11) равна

.                                                        (1.13)

Подставляя значение  в уравнение траектории (1.10), определим ординату вершины

  (1.14)

Из (1.14) видно: максимальная высота полета ОД (рис. 1.12) обеспечивается, когда , т.е. при , и равна

.                                                   (1.14,а)

Отметим, что расстояние от начала координат до максимально возможной высоты полета зависит только от величины скорости.

Определим время , в течение которого тело поднимается вверх. Для этого достаточно решить уравнение , т.к. в тот момент, когда  достигнет наибольшего значения, проекция скорости на эту ось равна нулю, т.е.

Итак, используя второе уравнение из (1.9), имеем

,

откуда

.                                                      (1”)

Полное время полета  определим исходя из того, что полет прекращается в тот момент, когда . Пользуясь первым уравнением в (1.9) и (1.12), находим

,

 откуда 

.                                                        (2”)

Сравнивая выражения (1”) и (2”), видно, что при любом угле наклона броска материальной точки полное время  полета в 2 раза больше времени  подъема.

1. 4 .2.Парабола безопасности

Проведем исследование движения тела (1.9) меняя углы наклона начальной скорости . Если при заданном значении начальной скорости  тела менять угол наклона начальной скорости  (формулы (1.9 – 1.10)), то получим множество разных траекторий снаряда (рис. 1.13).

Максимальная дальность полета снаряда по горизонтали  достигается при =45⁰, а максимальная высота полета равна при =90⁰.

Уравнение параболы, проходящей через точки D и С (рис. 1.13), имеет вид

.                                         (1.15)

Эта парабола называется  параболой безопасности.

При этом все траектории, отвечающие значениям , заключенным в интервале , будут находиться внутри этой параболы.

Действительно, решая совместно уравнения (1.10) и (1.15), находим, что соответствующие линии (траектория полета и парабола безопасности) имеют единственную общую точку с координатами

1. 4. 2.  Движение снаряда в сопротивляющейся среде

Рассмотрим задачу о полете снаряда, выброшенного из орудия с начальной скоростью  под углом  к горизонту. Примем точку вылета из ствола за начало координат, ось у направим вертикально вверх, ось х будем считать горизонтальной (рис. 1.14).

Силу сопротивления воздуха примем пропорциональной скорости, т.е.

. Для определенности предположим, что начальная скорость  располагается в плоскости хoу.

Дифференциальный закон движения точки имеет вид

                                                     (1.16)

Вектора  и  в формуле (1.16) имеют, в общем случае, по три проекции:  и .

Тогда проекции векторного уравнения (1.16) на декартовы оси координат,  имеют вид

 (1.16,а)

На снаряд действуют две силы: сила тяжести снаряда , направленная вдоль оси у вниз, и сила сопротивления , направление которой противоположно направлению скорости (рис. 1.14); их равнодействующая , (сила, действующая на снаряд), равна их геометрической сумме этих сил:

.

Проекции силы  на декартовы оси координат, запишутся

. (1.17)

Тогда уравнения движения (1.16,а), учитывая (1.17), примут вид

.      (1.18)

Запишем начальные условия задачи:

при t = 0, 

    (1.19)

где  - модуль начальной скорости снаряда.

После преобразования и сокращения на m, дифференциальные уравнения (1.18) примут вид

                    (1.20)

Получили дифференциальные уравнения с неразделенными переменными.

Разделим переменные в каждом из уравнений (1.20):

Проинтегрируем каждое из этих уравнений, с учетом начальных условий (1.19), получим

 

После потенцирования уравнений, имеем:

                  

Подставляя значения начальных условий задачи  (1.19), получаем

       (а)

Последние формулы дают возможность определить скорость снаряда в любой момент времени. Из них следует, что снаряд летит в плоскости хОу, поскольку .

Для определения перемещений х и у вдоль координатных осей воспользуемся тем, что . Тогда, уравнения (а) примут вид

 (б)

Уравнения (б) снова разделились: первое из них связывает неизвестную функцию , а второе – функцию .

Разделяя переменные в уравнениях (б) и интегрируя с учетом начальных условий (1.19), находим:

Получили уравнения движения точки в плоскости в виде

              (1.21)

Формулы (1.21) дают возможность определить положение снаряда в любой момент времени.

На (рис. 1.15) представлены траектории движения снаряда с различными коэффициентами k, т.е. в средах различной плотности.

Путем предельного перехода при , получим уравнения движения снаряда под действием одной силы тяжести. Обозначим координаты в этом случае  и . При вычислении пределов используется формула разложения в ряд экспоненты

.

Для х(t) из (1.21) получаем

Бесплатная лекция: "2.1 История развития конфликтологических идей" также доступна.

Прежде чем переходить к пределу в  из (1.21), преобразуем выражение:

Тогда

Получили уравнения движения точки под действием одной силы тяжести, которые соответствуют полученным раньше (1.9).

Отметим, что траектории движения тела (1.21) не являются в точности параболами. В действительности траектории еще сложнее, поскольку снаряд при движении испытывает сопротивление воздуха; ускорение свободного падения g зависит от высоты над поверхностью Земли; определенные поправки в процесс попадания снаряда в цель вносит вращение Земли.

 При решении реальных задач всегда пренебрегают теми или иными факторами. Так, если при небольшой начальной скорости тела ()  роль сопротивления воздуха невелика, то при больших , например, при ,  сопротивлением воздуха пренебрегать нельзя; сопротивление воздуха уменьшает дальность полета снаряда от получающегося по формуле (1.11) значения 61 км  до 22,2 км по формулам (1.21).