Анализ точности импульсных систем

Точность воспроизведения входных воздействий является одной из наиболее важных характеристик импульсных систем. При исследовании точности автоматических систем обычно рассматривают вынужденные процессы, то есть, процессы устанавливающиеся по истечении бесконечно большого промежутка времени после подачи входного воздействия. Рассмотрим, как определяются вынужденные процессы в импульсных системах.

Реакция импульсной системы (безразлично, замкнутой или разомкнутой) на входное воздействие f[kT] определяется соотношением:

, (21.1)

где w[kT] - импульсная переходная функция системы, связанная с ее z- передаточной функцией зависимостью:

w[kT]=Z^-1{w(z)}.

Формула (21.1) записана в предположении, что входное воздействие приложено в момент времени k=0. Если же входное воздействие приложено в произвольный момент времени k=k₀, то выражение (21.1) примет вид:

Пусть , то есть между моментом приложения входного воздействия и моментом наблюдения прошло бесконечно большое время. Такой процесс в системе мы назовем вынужденным и обозначим его через x_в[kT]. Тогда:

. (21.2)

Проведем замену переменных по формуле k-i=j. Тогда выражение (21.2) трансформируется в следующее выражение для вынужденного процесса:

. (21.3)

Разность между общим процессом (21.1) и вынужденным процессом (21.3) определяет свободный процесс импульсной системы x_c[kT]:

x_c[kT]=x[kT]-x_в[kT],

или, с учетом (21.1) и (21.3):

Таким образом, свободный процесс определяет отклонение общего процесса в импульсной системе от вынужденного.

Вернемся к формуле (21.3). Разложим входное воздействие в ряд Тейлора по переменной jТ в окрестности точки kT:

, (21.4)

где .

Подставив выражение (21.4) в формулу (21.7), получим:

Обозначим: и назовем эту величину моментом r-ого порядка весовой характеристики w[kT].

Тогда выражение для вынужденного процесса в системе приобретает вид:

. (21.5)

Числа d₀, d₁, ... характеризуют дискретную систему и могут быть вычислены заранее. Производные также легко определяются (особенно это просто делается для степенных входных воздействий) и, таким образом, зависимость (21.5) позволяет построить вынужденные процессы в системе.

Для определения моментов d₀, d₁, ... можно использовать следующую формулу:

где W^*(p) - передаточная функция импульсной системы, соответствующая дискретному преобразованию Лапласа:

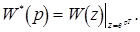
Указанная зависимость получается r- кратным дифференцированием формулы D- преобразования функции w[kT] :

с последующей подстановкой p=0 .

Протекание переходных процессов в ИС имеет свои особенности. В частности, здесь оказываются возможными процессы, затухающие за конечное время, так называемые процессы конечной длительности. Определим условия их возникновения в дискретной системе с передаточной функцией W(z). Рассмотрим импульсную переходную функцию w[kT] и установим, когда возможно выполнение равенства:

w[kT]=0, k>k₀ . (21.6).

Пусть передаточная функция W(z) является дробно-рациональным выражением, то есть:

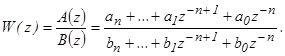
Функции w[kT] и W(z) связаны между собой z- преобразованием, то есть с учетом равенства (21.6):

. (21.7)

Очевидно, что равенство (21.7) возможно при выполнении условий:

. (21.8)

Таким образом, выполнение условий (21.8) влечет за собой выполнение равенства (21.6). С учетом равенства (21.6) при k₀=n из выражения (21.1) имеем:

x_c[kT]=0, k=n,n+1...,

то есть свободные процессы в системе заканчиваются за n- шагов квантования, где n- порядок системы.

После этого в системе устанавливается вынужденный процесс x_в[kT]. Наличие процессов с конечной длительностью, то есть выполнение условий (21.8), обеспечивается надлежащим выбором параметров исходной системы или параметров дополнительного корректирующего устройства. Отметим, что характеристическое уравнение такой системы имеет вид:

в_nzⁿ=0,

то есть устойчивость такой системы гарантируется.

21.2. АНАЛИЗ ТОЧНОСТИ ПРИ ПОЛИНОМИАЛЬНЫХ (СТЕПЕННЫХ) ВОЗДЕЙСТВИЯХ.

Рассмотрим вынужденные процессы, возникающие в дискретных системах при степенных воздействиях, и оценим точность воспроизведения входного сигнала.

Пусть входной сигнал является постоянным, то есть f[kT]=A=const

Определим вынужденный процесс:

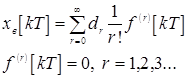
тогда: х_в[kT]=d₀A.

В соответствии с формулой , имеем , то есть вынужденный процесс при постоянном входном воздействии также является постоянной величиной.

Пусть входной сигнал:

f[kT]=A*kT,

изменяется по линейному закону. Тогда Для вынужденного процесса (21.5) получаем:

х_в[kT]=d₀AkT+d₁A,

где d₀=W^*(0), ;

то есть вынужденный процесс при линейном входном воздействии является также сигналом, изменяющимся по линейному закону, параметры которого определяются коэффициентами передаточной функции системы.

Продолжая рассмотрение, можно прийти к следующему результату: вынужденный процесс при степенном воздействии является полиномом той же степени, что и входной сигнал. Коэффициенты этого полинома определяются коэффициентами входного воздействия и параметрами передаточной функции системы.

Рассмотрим замкнутую импульсную систему, структурная схема которой представлена на рис.21.1.

Рис.21.1.

Оценим точность воспроизведения системой полиномиального входного воздействия:

f[kT]=A₀+A₁(kT)+...+A_e(kT)^e (21.9),

для чего рассмотрим установившуюся ошибку системы .

Рассматривая z-ПФ дискретных систем, легко видеть, что порядок астатизма дискретной системы (то есть порядок полюса z=1 передаточной функции W(z)) совпадает с порядком астатизма приведенной непрерывной части системы. Если порядок астатизма дискретной системы равен r, то ее z-ПФ может быть записана в виде:

(21.9),

где - не имеет в точке z=1 ни нулей, ни полюсов.

Так как ПФ замкнутой системы по ошибке определяется соотношением:

то с использованием зависимости (21.9) найдем:

где .

Тогда по теореме о предельном значении решетчатой функции для сигнала ошибки можно записать:

. (21.10)

В последнем выражении в точке z=1 не имеет ни нулей, ни полюсов.

F(z) - z- преобразование входного воздействия. Для функции (21.4) z- преобразование определится формулой:

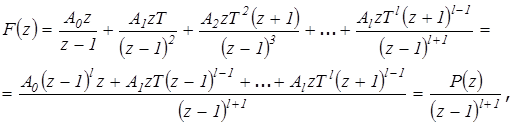
где - полином степени l, причем P(1)0.

Тогда зависимость (21.10) может быть представлена в следующем виде:

Из полученной формулы следует, что могут иметь место три случая:

1. r<l - порядок астатизма меньше степени полинома входного воздействия. Тогда , то есть ошибка неограниченно увеличивается с течением времени.

2. r=l- порядок астатизма равен степени полинома входного воздействия.

Тогда , то есть установившееся значение ошибки является постоянной величиной, отличной от нуля.

3. r>l- порядок астатизма больше степени полинома входного воздействия. Тогда , то есть в этом случае установившееся значение ошибки равно нулю.

Если система является статической (r=0), то установившаяся ошибка при отработке ступенчатого входного сигнала:

, и, тогда .

Величина представляет собой коэффициент передачи разомкнутой системы К. Нетрудно показать, что для случая экстраполятора нулевого порядка он совпадает со значением коэффициента передачи приведенной непрерывной части К_НЧ. Таким образом, установившаяся ошибка статической системы на постоянный сигнал определяется по выражению:

Для системы с астатизмом первого порядка (r=1) установившаяся ошибка на линейно- нарастающий сигнал f[kT]=a₀+a₁(kT) определяется по выражению:

или, аналогично предыдущему случаю: , где К=W₀(1)- коэффициент передачи системы по скорости.

21.3. КОЭФФИЦИЕНТЫ ОШИБОК ДИСКРЕТНОЙ СИСТЕМЫ.

При анализе точности непрерывных систем при полиномиальных (степенных) входных воздействиях успешно применяется метод коэффициентов ошибок. Этот же метод может использоваться и для дискретных автоматических систем.

КОЭФФИЦИЕНТЫ ОШИБОК В НЕПРЕРЫВНЫХ СИСТЕМАХ.

Допустим, входная функция g(t) имеет ограниченное число производных (до m- порядка). В этом случае ошибку системы можно определить следующим образом:

Раскладываем ПФ по ошибке в ряд по степеням р:

Перейдем к оригиналу:

Величины с₀, с₁, ..., с_m- коэффициенты ошибок. Они могут определяться согласно общему правилу разложения функции в ряд Тейлора по формулам:

причем коэффициент с₀ отличен от нуля только в статических системах.

В системах с астатизмом первого порядка с₀=0, а коэффициент с₁ связан с добротностью по скорости соотношением: и т.д.

Если управляющее воздействие имеет ограниченное число производных, то рассматриваемый ряд будет иметь ограниченное число членов.

Вернемся к рассмотрению точности импульсных систем.

Из изложенного ранее материала следует, что выражение для сигнала ошибки импульсной системы в вынужденном процессе может быть записано в виде:

, (21.11)

где - импульсная переходная функция замкнутой системы по ошибке.

Выразим решетчатую функцию через ее разности конечного порядка, в частности, для i=1,2,3 , получим:

;

В общем случае, для i- ого порядка:

, (21.12)

где .

Подставляя выражение (21.12) в (21.11), получим:

Группируя в этом выражении слагаемые, соответствующие разностям , будем иметь:

. (21.14)

Введем коэффициенты с_j, определяемые соотношениями:

, (21.15)

где i⁽^j⁾=i*(i-1)*…*(i-j+1).

Тогда выражение (21.14) приобретает вид:

, (21.16)

то есть величина вынужденной ошибки в системе полностью определяется введенными коэффициентами С_j и разностями квантованного входного сигнала.

Выражение (21.6) позволяет вычислить установившуюся ошибку системы в зависимости от разностей входного сигнала. Пусть, например,

Тогда:

;

Коэффициенты С_j - называются коэффициентами ошибок дискретной системы. Они могут быть вычислены заранее по передаточной функции замкнутой системы :

Дифференцируя эту зависимость по z, получим для j- производной:

Сравнивая полученное выражение с формулой (21.15), получим:

. (21.17)

При вычислении коэффициентов ошибок производные обычно находят не непосредственным дифференцированием, а определяя коэффициенты разложения функции в ряд Тейлора по степеням (z-1).

Действительно, данное разложение имеет вид:

Коэффициенты данного разложения легко находятся переходом от переменной z к новой переменной и последующим делением числителя полученного дробно- рационального выражения на знаменатель.

Рассмотрим пример:

Определим ошибку, устанавливающуюся в импульсной системе, если:

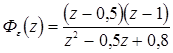
и f[kT]=a₀+a₁kT, a₀=2, a₁=4, T=1.

Введем новую переменную , получим:

Проводящая система сердца - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

(21.18)

Разделив числитель и знаменатель, найдем разложение функции (21.18) в ряд по степеням (запишем только два первых члена):

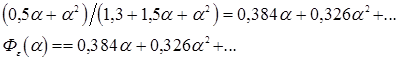
Откуда следует, что с₀=0; с₁=0,384; с₂=0,326 и тогда:

Таким образом, мы рассмотрели, как оценивается точность импульсных систем при степенных входных воздействиях. В случае необходимости проведения анализа точности при гармоническом входном сигнале он выполняется с помощью псевдочастотных ЛАФЧХ импульсной системы совершенно аналогично тому, как это делалось для непрерывных систем. При этом для перехода от ЛАФЧХ разомкнутой дискретной системы к ЧХ по сигналу ошибки могут использоваться те же номограммы замыкания, что и для непрерывных систем.

Поделитесь ссылкой:

Популярные услуги

Анализ точности импульсных систем

Рекомендуемые материалы

Рекомендуемые лекции