Нестационарные итерационные методы

4. Нестационарные итерационные методы

В разделе 3 были изучены некоторые простейшие стационарные методы, т.е. такие методы, у которых итерационные параметры () не зависят от номера итерации. Ясно, что можно попытаться ускорить сходимость, если выбирать их по-разному на каждой итерации:

                                                                 (4.1)

Градиентные методы решения задачи  характеризуются тем, что у них оператор  постоянный, а параметр экстраполяции  (или шаг) меняется на каждой итерации.

Название происходит от того, что исходная задача эквивалентна минимизации функционала

                                                   (4.2)

Очевидно, при  квадратичный функционал (4.2) ограничен снизу нулем, и достигает минимума на точном решении  задачи . Преобразуем (4.2).

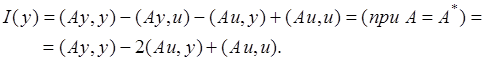
Поскольку , а , то минимум функционала  совпадает с минимумом функционала

Рекомендуемые материалы

                                           (4.3)

Дополнительные сведения из математики.

Градиент произвольного функционала  в точке  определяется через производную Гато (производная, вычисленная в точке  по направлению , или дифференциал Гато, типа  для функций)

                             .

, как разность функционалов, сам является функционалом.

Очевидно, если  - линейный функционал, то производная Гато совпадает с ним:

                                   .

Это значит, что  для линейного функционала не зависит от , и его производная Гато постоянна в любой точке.

Пример 1. Рассмотрим нелинейный функционал . Вычислим его производную Гато

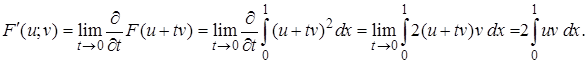
Он всегда линеен по , но зависит от точки .

Пример 2.  Пусть линейный функционал  Тогда

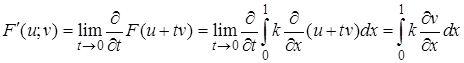
1.6 Интеграционные процессы в менеджменте - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Он совпадает с  и не зависит от .

Градиентом функционала  в точке , определенного в пространстве функций  со скалярным произведением  называется функция , такая, что .

Для функционала (4.3) имеем

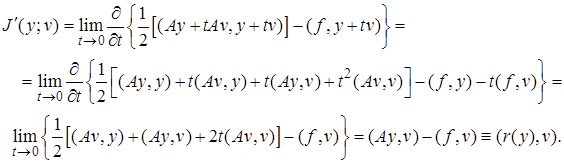
Здесь  - невязка исходного уравнения, которая совпадает с .

Геометрически это значит, что в точке  направление невязки  ортогонально линии , а функционал (4.3) быстрее всего растет в этом направлении; соответственно быстрее всего он убывает в направлении .