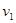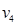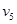Порождающие системы
Лекция 9
4. Порождающие системы
4.1 Системы с поведением
Термин поведение используется для характеристики общего параметрически инвариантного ограничения на переменные обобщенной представляющей системы и, может быть, на некоторые дополнительные абстрактные переменные. Дополнительные переменные определяются на параметрическом множестве с помощью правил сдвига.
Так как описание параметрически инвариантного ограничения на рассматриваемые переменные может быть использовано для порождения состояний переменных при данном параметрическом множестве, системы, содержащие такие ограничения, называются порождающими системами. Поведение представляет собой одну из форм задания этого ограничения.
Для заданной обобщенной представляющей системы диапазон возможных типов параметрически инвариантных ограничений зависит от свойств, приписываемых параметрическому множеству. Если на этом множестве никаких свойств не определено (как это часто бывает для групп), то состояния переменных могут ограничивать только друг друга. Однако если параметрическое множество упорядочено, состояния переменных могут ограничиваться не только другими состояниями, но и состояниями выбранного соседства для каждого конкретного значения параметра.
Соседство на упорядоченном параметрическом множестве обычно называется маской и определяется через переменные, параметрическое множество и набор правил сдвига на параметрическом множестве. Правило сдвига, скажем правило  ,— это однозначная функция
,— это однозначная функция
Рекомендуемые материалы
 , (4.1)
, (4.1)
которая каждому элементу W ставит в соответствие другой (причем единственный) элемент W. Если, например, параметрическое множество полностью упорядочено (как в случаях, когда рассматривается время или одновременное пространство) и представляет собой множество последовательных целых положительных чисел, то любое правило сдвига может быть задано простым уравнением
 , (4.2)
, (4.2)
где  — целая константа (положительная, отрицательная или нуль). При
— целая константа (положительная, отрицательная или нуль). При 
 называется тождественным правилом сдвига.
называется тождественным правилом сдвига.
Все выше сказанное, можно пояснить следующим образом. Для того чтобы система, была способна генерировать данные, из исходных данных, нужно определить некоторые правила по которым будут получаться новые данные. В узком смысле это будут некоторые функции. Например, линейная функция одной переменной – геометрически прямая. Эта функция преобразует значение аргумента, в некоторое значение. В более широком смысле это параметрически инвариантное ограничение.
4.2 Выборочные переменные и маски
Пусть задана обобщенная представляющая система I, определяемая уравнением (2.12). Обозначим через V множество переменных из I, а через R набор правил сдвига, рассматриваемых для этих переменных. Тогда множество переменных
 ,(4.3)
,(4.3)
называемых выборочными переменными, может быть введено с помощью уравнений
 ,(4.4)
,(4.4)
для некоторых переменных  и правил сдвига
и правил сдвига  ;
;  обозначает состояние выборочной переменной
обозначает состояние выборочной переменной  при значении параметра w, а
при значении параметра w, а  — состояние переменной
— состояние переменной  при значении параметра
при значении параметра  , т. е. при значении, полученном для заданного w, при применении правила сдвига
, т. е. при значении, полученном для заданного w, при применении правила сдвига  . Для полностью упорядоченного параметрического множества, правила сдвига которого имеют вид (4.2), уравнение (4.4) может быть переписано в более определенном виде
. Для полностью упорядоченного параметрического множества, правила сдвига которого имеют вид (4.2), уравнение (4.4) может быть переписано в более определенном виде
 ,(4.5)
,(4.5)
Так как любое правило сдвига из набора R может быть применено к любой переменной из множества V, то множество всех возможных выборочных переменных представляется декартовым произведением  . В действительности рассматриваются выборочные переменные, характеризуемые отношением
. В действительности рассматриваются выборочные переменные, характеризуемые отношением
 , (4.6)
, (4.6)
так, что всякой паре  соответствует одно уравнение из (4.4). Отношение М представляет схему соседства на параметрическом множестве, в терминах которого определены выборочные переменные. Эта схема обычно называется маской.
соответствует одно уравнение из (4.4). Отношение М представляет схему соседства на параметрическом множестве, в терминах которого определены выборочные переменные. Эта схема обычно называется маской.
Для введения идентификаторов выборочных переменных k должна быть введена некая однозначная функция (кодирование).
 , (4.7)
, (4.7)
где  — это количество элементов множества М.
— это количество элементов множества М.
Если выборочная переменная  определена через переменную
определена через переменную  и некоторое правило сдвига согласно уравнению (4.4), то множество состояний
и некоторое правило сдвига согласно уравнению (4.4), то множество состояний  , очевидно, То же самое, что и множество состояний
, очевидно, То же самое, что и множество состояний  т. е.
т. е.  . Однако для удобства обозначений будем множество состояний выборочной переменной обозначать
. Однако для удобства обозначений будем множество состояний выборочной переменной обозначать  ; смысл любого
; смысл любого  однозначно определяется маской в терминах одного из множеств
однозначно определяется маской в терминах одного из множеств  . Таким образом, декартово произведение
. Таким образом, декартово произведение
 ,(4.8)
,(4.8)
представляет собой полное множество состояний выборочных переменных.
4.3 Маски в случае полностью упорядоченных параметрических множеств
Рассмотрим сначала понятие маски и связанное с ним поведение представляющих систем для полностью упорядоченных параметрических множеств, а затем распространим его на частично упорядоченные параметрические множества. Обозначим полностью упорядоченные параметрические множества  , а их элементы
, а их элементы  . При этом уравнение (4.4) немного изменится:
. При этом уравнение (4.4) немного изменится:
 , (4.9)
, (4.9)
Для полностью упорядоченных параметрических множеств маска может быть изображена в виде вырезки из матрицы, представляющей декартово произведение  .Это показано на рис.4.1,а, на котором строки помечены идентификаторами
.Это показано на рис.4.1,а, на котором строки помечены идентификаторами 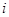
|
 | = |
| = | 2 | ||
|
| = |
| = | 0 | ||
|
  | = |
| = | 3 | ||
|
| = |
| = | 2 | ||
|
| = |
| = | 1 | ||
|
| = |
| = | 1 | ||
|
 | = |
| = | 0 | ||
| | = |
| = | 3 | ||
| | = |
| = | 0 | ||
|
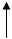  | = |
| = | 2 |
|
| -2 | -1 | 0 | 1 |
| i=1 | 1 | 2 |
| |
| 2 | 3 | 4 | ||
| 3 | 5 | 6 | 7 | |
|
| 8 | 9 | ||
| 5 | 10 |
в) а)
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … | ||
|
| 0 | 0 | 1 | 2 | 2 | 2 | 0 | 1 | 1 | |||
|
| 3 | 2 | 2 | 1 | 2 | 3 | 3 | 2 | 0 | |||
|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||
|
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | 1 | 2 | |||
|
| 2 | 2 | 2 | 0 | 1 | 2 | 2 | 2 | 1 |
|
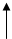
б)
Рис.4.1. Пояснение понятия маски для полностью упорядоченных параметрических множеств.
переменных из множества V, a столбцы — целыми константами  , связанными с правилами сдвига вида (4.2). Элементы матрицы или пусты, или представляют собой идентификаторы k выборочных переменных, приписанные парам
, связанными с правилами сдвига вида (4.2). Элементы матрицы или пусты, или представляют собой идентификаторы k выборочных переменных, приписанные парам  согласно (4.6); пустые элементы матрицы соответствуют элементам
согласно (4.6); пустые элементы матрицы соответствуют элементам  , не входящим в маску. В визуальном представлении становится ясно, почему используется термин «маска».
, не входящим в маску. В визуальном представлении становится ясно, почему используется термин «маска».
Часто бывает удобно разбить маску М на подмаски М„ каждая из которых связана с одной переменной и, из подобной системы. Формально
13 Фрактальные алгоритмы - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
 , (4.10)
, (4.10)
В визуальном (матричном) представлении  подмаски
подмаски  представляют собой строки. В любой маске один столбец соответствует тождественному правилу сдвига
представляют собой строки. В любой маске один столбец соответствует тождественному правилу сдвига  . Этот столбец имеет особое значение, поскольку связанные с ним выборочные переменные идентичны базовым переменным заданной представляющей системы. Будем этот столбец в масках называть справочником. Если маска помещена на матрицу данных таким образом, что справочник совпадает с определенным значением t, то маска выделит только некоторое подмножество элементов, а именно элементы, представляющие полное состояние выборочных переменных при данном значении t. Так, например, на рис. 4.1,б изображена маска (определенная на рис. 4.1,а), помещенная на матрицу данных d при t=7 (справочник маски совпадает с t=7). Полное состояние выборочных переменных для этого положения маски показано на рис. 4.1,в. Состояния справочника выборочных переменных
. Этот столбец имеет особое значение, поскольку связанные с ним выборочные переменные идентичны базовым переменным заданной представляющей системы. Будем этот столбец в масках называть справочником. Если маска помещена на матрицу данных таким образом, что справочник совпадает с определенным значением t, то маска выделит только некоторое подмножество элементов, а именно элементы, представляющие полное состояние выборочных переменных при данном значении t. Так, например, на рис. 4.1,б изображена маска (определенная на рис. 4.1,а), помещенная на матрицу данных d при t=7 (справочник маски совпадает с t=7). Полное состояние выборочных переменных для этого положения маски показано на рис. 4.1,в. Состояния справочника выборочных переменных  в точности те же (для любого t), что и состояние базовых переменных соответственно
в точности те же (для любого t), что и состояние базовых переменных соответственно  . Остальные выборочные переменные представляют собой состояния из параметрического соседства в t. Для любой маски при любом t схема соседства сохраняется. Если t — время, то переменная
. Остальные выборочные переменные представляют собой состояния из параметрического соседства в t. Для любой маски при любом t схема соседства сохраняется. Если t — время, то переменная  будет представлять будущее (относительно рассматриваемого значения t) состояние переменной
будет представлять будущее (относительно рассматриваемого значения t) состояние переменной  , а переменные
, а переменные  и
и  будут представлять, прошлые состояния переменной
будут представлять, прошлые состояния переменной  любая маска представляет определенную точку зрения, в соответствии с которой представляются ограничения на базовые переменные.
любая маска представляет определенную точку зрения, в соответствии с которой представляются ограничения на базовые переменные.
К.Р. № 9
Опишите систему с поведением в случае полностью упорядоченных параметрических множеств. (Обязательно необходимо указать маски и выборочные переменные.)



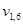
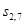
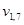
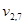
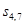
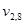
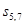
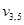
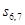
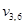
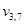
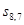
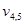
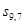

 4
4