Решение дифференциальных уравнений

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальное уравнение – это соотношение вида

                                         (7.1)

Здесь:  - независимая переменная (аргумент),  – искомая функция этого аргумента,  – производные искомой функции. Левая часть равенства (7.1) представляет собой непрерывную функцию своих аргументов.

Порядок старшей производной, входящей в уравнение (7.1), называют порядком дифференциального уравнения. В естественных науках и технических приложениях чаще встречаются уравнения первого порядка

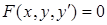
и уравнения второго порядка

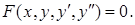
Решить уравнение (7.1) – значит найти функцию, которая при подстановке в дифференциальное уравнение обращает последнее в тождество при всех допустимых значениях аргумента. Таких функций оказывается не одна, а целое семейство. При этом мы находим общее решение дифференциального уравнения. Это решение можно представить в виде

Рекомендуемые материалы

                                              (7.2)

Здесь  – произвольные постоянные интегрирования, число которых совпадает с порядком уравнения. Искомое семейство функций может быть также найдено в неявном виде:

                                          (7.3)

Равенство (7.3) определяет общий интеграл дифференциального уравнения.

Числовые значения констант интегрирования определяются, если наряду с уравнением (7.1) заданы начальные условия

              (7.4)

Число начальных условий должно равняться порядку уравнения. В начальных условиях могут быть заданы значения искомой функции, а также её производных, порядок которых меньше порядка дифференциального уравнения. Уравнение (7.1) вместе с начальными условиями (7.4) представляют собой задачу с начальными условиями. При решении такой задачи сперва получается общее решение (7.2), затем на основании условий (7.4) составляется система уравнений относительно неизвестных . Решение этой системы  подставляется в общее решение (7.2). Это позволяет построить частное решение уравнения (7.1), удовлетворяющее начальным условиям (7.4). Частное решение представляет собой определенную функцию аргумента . Эта функция может быть задана неявно. В этом случае получается частный интеграл дифференциального уравнения.

Вопросы существования и единственности решения задачи с начальными условиями полно рассмотрены в учебной литературе. В рамках данных методических указаний заметим только, что в большинстве задач, связанных с инженерными приложениями, существуют решения, причем единственные.

Далее рассматриваются решения типовых задач.

Пример 7.1: Линейное уравнение первого порядка. Метод вариации произвольной постоянной

Пусть требуется найти решение дифференциального уравнения

                                           (7.5)

удовлетворяющее начальному условию

                                                 (7.6)

Примечание: Уравнение (7.5) содержит искомую функцию  и ее производную  первой степенью. Таким образом, уравнение (7.5) – линейное уравнение первого порядка. Наличие свободного слагаемого делает уравнение неоднородным.

1. Рассмотрим соответствующее однородное уравнение

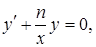
которое можно проинтегрировать, разделив переменные:

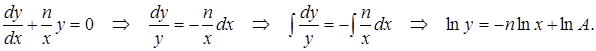
В результате получим

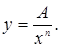
2. Используем полученное общее решение однородного уравнения. Будем искать общее решение данного неоднородного уравнения в виде

                                            (7.7)

Примечание: Подстановка на место постоянной  неизвестной функции  называется вариацией произвольной постоянной.

Подставляя выражение (7.7) в уравнение (7.5), получим:

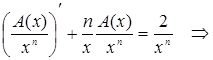
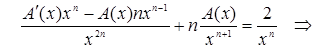
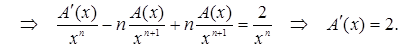
Интегрируем полученное уравнение, разделяя переменные:

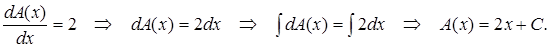
Подставляя последнее выражение в равенство (7.7), получим:

                                    (7.8)

В формуле (7.8) общее решение неоднородного уравнения представлено как сумма двух слагаемых: первое совпадает с общим решением однородного уравнения, второе является частным решением неоднородного уравнения.

3. Определим числовое значение постоянной  из начального условия (7.6):

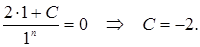
Тогда искомое решение задачи с начальным условием:

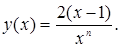
Пример 7.2: Линейное уравнение второго порядка с постоянными коэффициентами

Решение дифференциального уравнения

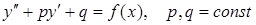
может быть получено как сумма общего решения соответствующего однородного уравнения

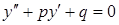
и частного решения данного неоднородного уравнения. Чтобы найти общее решение однородного уравнения, определим корни  характеристического уравнения

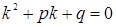
и применим одну из стандартных формул:

                          если           ,

                           если           ,

         если           .

Частное решение рекомендуется построить методом неопределенных коэффициентов, ориентируясь по виду функции  в правой части уравнения.

Рассмотрим далее следующую задачу: требуется найти общее решение дифференциального уравнения

                                       (7.9)

и частное решение, удовлетворяющее начальным условиям

                              (7.10)

1. Составим и решим характеристическое уравнение:

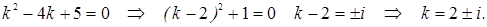
Тогда

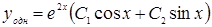
- общее решение однородного уравнения, соответствующего данному.

2. Исходя из вида правой части уравнения (7.9), будем искать частное решение этого уравнения в форме . Тогда:

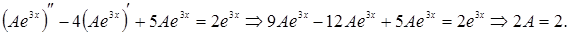
Получили , следовательно, .

3. Общее решение данного неоднородного уравнения представим в виде

.

В результате получим общее решение:

                         (7.11)

Дифференцируя выражение (7.11), находим:

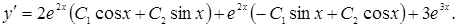
Учитываем начальные условия:

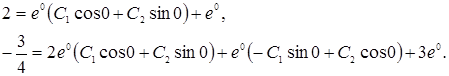
Тогда

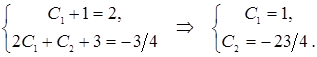
Получили частное решение, удовлетворяющее начальным условиям:

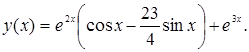
Пример 7.3: Система дифференциальных уравнений

Рассмотрим далее задачу об общем решении системы дифференциальных уравнений. Ограничимся случаем, когда выполняются следующие условия:

1) система содержит уравнения первого порядка, разрешенные относительно производных;

2) независимая переменная не входит явно в уравнения;

3) уравнения линейные с постоянными коэффициентами, однородные.

Система принимает вид

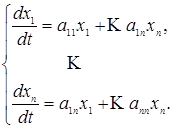
Через  обозначены искомые функции.

Возможна также матричная форма записи системы

                                           (7.12)

где

.

Общее решение системы (7.12) допускает представление

.                                    (7.13)

В формуле (7.13)  – произвольные постоянные интегрирования,  – линейно независимые частные решения системы. Частные решения можно найти в виде

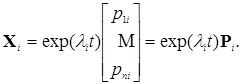
Здесь  – собственные числа матрицы , которые получаются как корни характеристического уравнения

.                                     (7.14)

Вектор-столбец  является ненулевым решением неопределенной системы линейных алгебраических уравнений.

                                      (7.15)

Пусть требуется найти общее решение системы дифференциальных уравнений

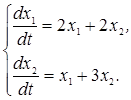
Характеристическое уравнение (7.14) принимает вид:

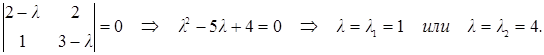
При  система (7.15) для рассматриваемой задачи принимает вид:

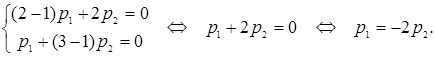
Полагая , получим . Возникает частное решение системы

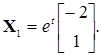
При  система (7.15) для рассматриваемой задачи принимает вид:

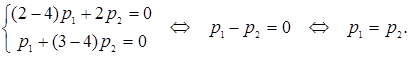
Полагая , получим . Возникает частное решение системы

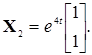
Используя выражение (7.13), построим общее решение сначала в матричном виде

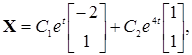
а затем в скалярной форме

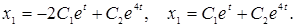
Пример 7.4: Уравнения, допускающие понижение порядка

1. Общее решение уравнения вида  можно получить путем повторного интегрирования правой части. Например,

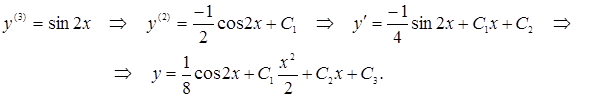
2. Общее решение уравнения вида  можно получить путем введения новой неизвестной функции

.                                          (7.16)

Для этой функции получается вспомогательное уравнение

,

Лекция "Свойства и виды устноречевой коммуникации" также может быть Вам полезна.

порядок которого меньше, чем порядок исходного уравнения. Получив общее решение вспомогательного уравнения, подставляем его в правую часть равенства (7.16). Затем восстанавливаем искомую функцию. Для этого интегрируем уравнение (7.16) так, как было показано в пункте 1.

Найдем далее общее решение уравнения:

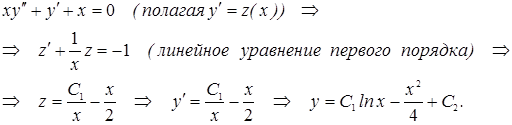
3. Уравнение вида  не содержит явным образом независимую переменную x. Порядок такого уравнения понижается на единицу, если принять, что . В качестве примера найдем общее решение уравнения:

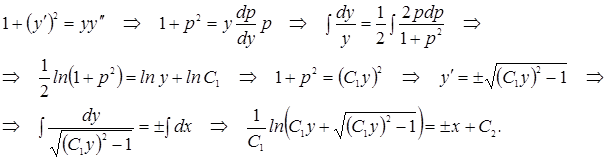
Получили общий интеграл данного уравнения.