Основные соотношения теории вероятностей

Основные соотношения теории вероятностей, как это ни   покажется парадоксальным, выглядят боолее естественно и гораздо более понятны, ее ли они рассматриваются не в дискретном, а в непрерывном выборочном пространстве, в котором определение вероятности дается через теорию меры и интегрирование. В связи с этим основные положения теории веро ятностей мы рассмотрим в пространстве Rⁿ. Как уже говорилось, в дискретных выборочных пространствах  вероятность приписывается веем подмножествам, в то время как в непрерывных пространствах подобный подход неприемлем, так как приводит к противоречиям.  Соответственно и не всякая функция на непрерывном пространстве может рассматриватьс. в качестве случайной величины. Для большинства приложений достаточно ограничиться  s-алгеброй борелевских множеств и беровскими функция ми, измеримыми относительно этой s-алгебры U.

Определение 2.1. Функция точки F(t) на прямой есть функция распределения  некоторой случайной величины, если она

а) неубывающая функция, т.е. F(a)£F(b)  при а < b ;

в) непрерывна справа, т.е.  F(а) = F(а+) ;

с) удовлетворяет условиям  F(- ¥ ) = 0,  F(¥) = I.

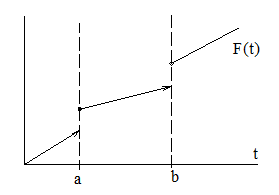
Между вероятностной мерой Р, определенной на s-алгебре подмно­жеств из R¹ и вероятностной функцией распределения  F(t) имеет место отношение

     F(t)=P{x £ t}.

Полагая t = а  и  t = b, получаем

Рекомендуемые материалы

     F(b)-F(a)=P{a<X£b}=P{(a,b]}

Вероятность попадания случайной величины Х в интервал (a,b]  можно также обозначать посредством. Соответственно, можно написать: F{(а,b]}=F(b)-F(a-), F{(a,b)]=F(b-)-F(a), F{[a,b)}=F(b-)-F(a-).

Понятие функции распределения можно обоощить и на многомерные про­странства. В Rⁿ функция распределения F(х) является функцией точки х = (х₁,..., х_n)ÎRⁿ. А в  общем случае можно показать, что  по заданной в Rⁿ функции  точки можно построить аддитивную функцию F{(a,b]} промежутка (а,в] по формуле

                                        (2.1)

где с = (с₁,..., с_n ) - это множество всех угловых точек промежутка

(а,в], т.е. точек  с_i=а_i, и с_j= b_j,  , а  l(c) - число входящих в  с  компонент а_j. Например, для пространства  R²  получаем

F{(а,b]} =  F(b₁,b₂) - F(а₁, b₂) - F(b₁,a₂) + F(а₁,а₂ ).

Понятно, что в многомерном случае функции распределения  становятся весьма неудобными для использования .  Из формулы (2.1) видно, что любая функция распределения порождает вероятностную меру  на s-алгебре борелевских множеств в Rⁿ .

Рассмотрим дискретные случайные величины, т.е. такие, которые при­нимают только конечное или счетное множество значений х₁, х₂, ..., х_n,...- с вероятностями  P_k>0, т.е. p_k=P{X=x_k}.  Расп­ределение подобных случайных величин описывается функцией

    

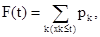
Легко видеть, что функция распределения дискретных случайных величин кусочно-постоянна и величина ее скачков в точках х_k равна F(x_k+0) - F(х_k - 0) = р_k .

Если же случайные величины непрерывно распределены на вещественной оси, то  функция их вероятностного распределения будет задаваться интегралом типа Лебега-Стилтьеса: 

    

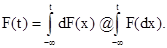
Очевидно,  F(¥) = I. Если же случайные величины распределены на некотором подмножестве   А  в R¹, то можно записать

    

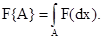
Если существует такая интегрируемая по Лебегу функция ¦(x), что

    

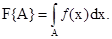
то говорят, что функция Fабсолютно непрерывна относительно меры Ле­бега, а функцию ¦(x)  называют плотностью  (или производной Радона-Никодима) функции F относительно меры Лебега. Согласно теореме Радона-Hикодима, распределение F абсолютно непрерывно относительно меры Лебега тогда и только тогда, когда для любых подмножеств A оси R¹ нуле вой длины оказывается F{A}=0.

Говорят, что вероятностное распределение F сингулярно относительно меры Лебега, если оно сосредоточено на множестве меры Лебега нуль т.е. на множестве нулевой протяженности.

Теорема Лебега о разложении. Любое вероятностное распределение F является смесью атомического (дискретного), абсолютно непрерывного и сингулярного непрерывного распределений.

Примером сингулярного непрерывного распределения является функция Кантора

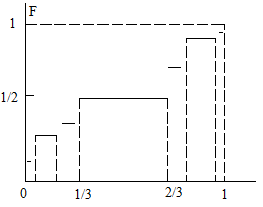
Эта функция является кусочно-постоянной, возрастающей лишь на множестве Лебега нуль, представляющем собой совершенное множество (замкнутое и плотное в себе), т.е. содер­жащее все свои предельные точки и одновременно содержащееся во множестве всех своих предельных точек, причем это совершенное множество нигде не плотно, т.е. его замыкание не содержит открытого множества.

Интеграл Лебега-Стилтьеса удовлетворяет всем свойствам обычного интеграла Лебега и для интегрируемых функций  U(х) записывается в виде (на Rⁿ) :

    

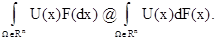
Для распределений в R¹ имеет место следующая формула интегрирования по частям:                                      

     

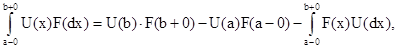
где в отношении функции U(х) предполагается, что она является функ­цией ограниченной вариации и непрерывна в тех точках в которых F(x) разрывна.

Если функция  U(х) непрерывна, а функция распределения F(х) терпит разрыв в точке сÎ(а,b), то имеет место представление:

    

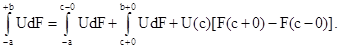
На практике редко когда бывает известно вероятностное распределе­ние случайной величины,и для получения всевозможного рода оценок пользуются некоторыми количественными характеристиками случайных величин, среди которых наиболее важны математическое ожидание, дис­персия и моменты различных порядков (³ 2).

Понятие математического ожидания, или среднего ожидаемого значения пришло из теории игр, где под этим понятием подразумевается ожидаемы выигрыш в игре. Определим это понятие сначала для дискретного случая Пусть w_i элементарные события из некоторого дискретного выборочного пространства W, вероятность появления i-го из которых имеет величину  р_i. Тогда  под математическим ожиданием cлучайной величины понимается величина E(х), определяемая рядом

    

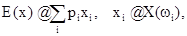
причем этот ряд предполагается абсолютно сходящимся. Если же ряд не сходится абсолютно, то операция усреднения (определения математичес­кого ожидания) теряет смысл.

Приведенное определение математического ожидания для дискретного ны борочного пространства нетрудно распространить на континуумиальные выборочные пространства, например, на подмножества W. Пространства Rⁿ Сначала это распространение целесообразно провести для случая наи­более простого представления случайной величины U, задаваемой сту­пенчатой функцией U(х), принимающей  значения  a₁,…,a_n .  По аналогии с дискретным случаем математическое ожидание будет задаваться

    

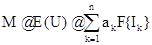
где I_k - интервалы, на которых функция U(х) принимает значения a_k, a F{I_k}- вероятности реализации значений  a_k .

Математическое ожидание  Е(U) обладает следующими свойствами:

а) Линейностью:  Е(a₁U₁+ a₂) = a₁Е (U1) + a₂Е(U₂);

в) Положительностью:    Е( U ) > 0  при U³0;

с) Нормированностью:    Е(1) = 1.

Вышеопределенное математическое ожидание Е(U) можно продолжить на более широкий класс функций с сохранением свойств а)-с). Известно, что непрерывные функции можно рассматривать как предел последователь­ности ступенчатых функций, a эти последние можно продолжить до бэровски функций. В этом случае математическое ожидание определяется при заме­не конечных сумм интегралом Лебега-Стилтьеса :

    

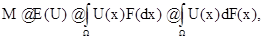
где предполагается абсолютная сходимость интеграла.

Из свойств интеграла следует, что математическое ожидание постоян­ной равно этой постоянной и математическое ожидание суммы случайных величин равно сумме их математических ожиданий. Столь же естественно из свойств интеграла следует, что математическое ожидание произведени независимых случайных величин равно произведению их математических ожиданий.

Математическое ожидание можно определить, вообще говоря, двумя способами. Выше мы определили его как интеграл , где F(х) - распределение вероятностей на множестве W. Однако  U(х), как функция переменной  х, распределенной по закону F(х) на множестве W, сама является случайной величиной, значения которой распределены на оси R¹ с некоторой вероятностью G(U), индуцируемой вероятностью F(х). Следовательно, математическое ожидание случайной величины Х = U(х)  можно также записать в виде

    

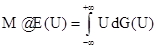
Наряду с математическим ожиданием, большую роль в приложениях иг­рает еще одна характеристика случайных величин - дисперсия, представ­ляющая собой математическое ожидание квадрата уклонения случайной ве­личины  Х = U(х) от ее математического ожидания М = E(U). Но опред лению, дисперсия D(Х) равна

    

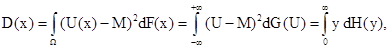
где F(х) - функция распределения на множестве W , G(U) –функция распределения значений  U(х)  и  Н(у) - функция распределения случайной величины (U - М)².

Очевидно, дисперсия постоянной величины С равна нулю.

Предложение 2.1. Дисперсия суммы двух независимых случайных величин Х и Y

равна сумме их дисперсий.

Доказательство. Из независимости Х и Y следует независимость также и разностей  (X - Е(Х))  и (Y - Е(Y)). Tогда утверждение следует из следующей цепочки элементарных преобразований:

     D(X + У) = Е[(Х+У - Е( Х+У)]²  = E[Х+У - Е(Х) - Е(У)]² = Е [(X - Е(Х))+ (У - Е(У))]² =

= DХ +DУ + 2 Е[(Х - Е(Х))( У - Е(У)] = DX + DУ + 2 Е(Х - Е(Х))·Е(У - Е(У)) .

                                                                                                  ë=0              ë=0

Следствие 2.1. Если X₁ ,..., X_n  - случайные величины, каждая из ко­торых независима от суммы  остальных, то дисперсия их суммы равна сум ме дисперсий каждой из них.

Следствие 2.2. дисперсия суммы конечного числа попарно независимых случайных величин Х₁,..., Х_n равна сумме их дисперсий.

Доказательство: 

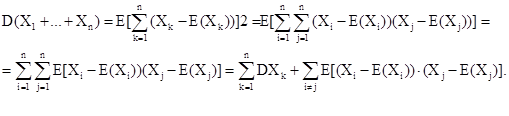
Нормированным уклонением случайной величины Х называется величина

    

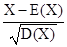
Если воспользоваться тем, что случайные величины Х и (постоянная) Е(Х

независимы и что дисперсия постоянной равна нулю, то можно получить:

    

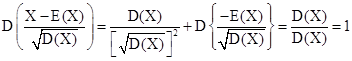
Нетрудно получить, что  D(Х - У) =D(X)+D(y), где Х и Y - независимые случайные величины. В самом деле, D(- Y) = (-1)² D(y) = D(Y)

В качестве аналога математического ожидания случайной величины мож но рассматривать  центр масс стержня неоднородной массы, а механичес­ким аналогом дисперсии может служить центральный момент инерции стержня. Чем больше масса стержня сосредоточена в окрестности его центра масс, тем  меньше  момент инерции, характеризующий разброс массы отно сительно центра масс; аналогично, с уменьшением разброса случайной величины относительно среднего значения уменьшается и дисперсия, ха­рактеризующая этот разброс.

На практике вместо дисперсии, имеющей размерность квадрата случай­ной величины, предпочитают пользоваться величиной

    

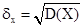
имеющей размерность самой случайной величины и называемой средним квадратическим отклонением.

Следует отметить, что  на практике нередко удобнее рассчитывать дисперсию не по формуле  Е( Х - Е(Х))² по формуле,а получающейся из нее после возведения в квадрат величины (X - Е(Х)) и  следующего уп­рощения  с использованием свойств математического ожидани

     D(Х) =  Е( Х² - 2 Х Е(Х) +[E(X)]²)= Е(Х²) - 2 Е(Х) Е(Х) +[Е(Х )]²= Е(Х²) – [Е(Х)]² .

Эта формула аналогична известной формуле механики, определяющей мо­мент инерции тела относительно любой оси через момент инерции относи­тельно параллельной оси, проходящей через центр масс тела.

В качестве примера вычислим математическое ожидание и дисперсию случайной величины Х , равномерно распределенной в интервале (а,b):

    

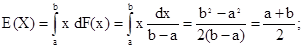
таким образом, математическое ожидание совпадает с серединой интервал подсчитаем теперь дисперсию по формуле: Е(Х² ) – [Е(Х)]² . Находим

    

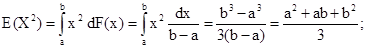
подставляя в формулу для дисперсии Е(Х)  и Е(Х²), получаем

    

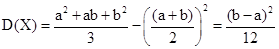
Отсюда видно, что чем больше длина интервала (а,b), на котором расп­ределена случайная величина X, тем больше дисперсия, т.е. дисперсия играет роль характеристики рассеяния случайной величины около матема­тического ожидания.

3.

Математическое ожидание и дисперсию называют также моментами пер­вого и второго порядка случайной величины X.  Для многих приложений важны не только первые два момента, но и моменты более высоких поряд­ков. Моментом  к-го порядка случайной величины Х называется математическое ожидание величины (X - а)^k , т.е.

    

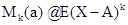
Если  а = 0, то момент называется начальным. Начальный момент первого порядка есть, очевидно, математическое ожидание. Если  а = Е(X), то момент называется центральным. Нетрудно убедиться, что центральный момент первого порядка равен нулю, а  центральный момент второго по­рядка есть дисперсия. Между центральными и начальными моментами  суще ствуют относительно простые полиномиальные зависимости, которые могут быть получены в результате выполнения операций вычисления степеней, входящих в определение этих моментов. Несколько первых центральных и начальных моментов играют большую роль в статистике. Например, если известен закон распределения случайной величины с точностью до нескол ких постоянных, то эти постоянные могут быть найдены во многих случая с помощью  нескольких первых моментов.  Если же функция распределена неизвестна, то даже с помощью всех целочисленных моментов не представ ляется возможным ее определить,  поскольку один и тот же набор счет­ного числа целочисленных моментов может относиться к различным функ­циям распределения. В связи с этим возникает проблема моментов; дана последовательность чисел     с₀ = I, с₁ , с₂ ....  и требуется найти, при каких условиях  существует такая функция распределения F(х), для ко­торой при всех n имеют, место равенства  и когда эта функция единственна? В настоящее время эта задача решена.

Дадим определение дисперсии n - случайных величин (Х₁ , ..., Х_n ), или , что то же самое,      n-мерной случайной величины (Х₁,…, X_n ). Дисперсией (или корреляционной матрицей) n-мерной случайной величины называется совокупность n² чисел, определяемых по формулам:

    

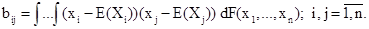
Числа и представляют собой элементы неотрицательно определенной матрицы

            ,

диагональные элементы которой, как легко видеть, представляют собой дисперсии соответствующих случайных величин: b_ij = D(X_i).

Числа b_ij при i¹j называются смешанными центральными моментами второго порядка случайных величин X_i, и X_j, . Очевидно, bij=bji. Коэфициенты b_ij обычно называют коэффициентами ковариации, а нормированные следующим образом коэффициенты ковариации

    

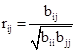
называют коэффициентами корреляции между случайными величинами Х_i и Х_j

Значения коэффициентов r_ij лежат в диапазоне [-1, 1] , причем значения  ±1  достигаются только в случае линейной зависимости между X_i, и X_j, что нетрудно подсчитать непосредственно. В самом деле,

а следовательно, r_ijÎ[-1,1].

Равенство r_ij = 1 возможно в том и только том случае, если

    

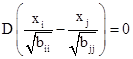
поскольку это равенство имеет место одновременно с равенством (I - r_ij) = 0. Но дисперсия равна нулю только от постоянной величины следовательно,

    

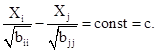
A последнее равенство выражает линейную связь между.  Аналогичная линейная связь лишь со знаком  + вместо  -  в левой части имеет место для случая r_ij= - I.

Задав линейную связь между Х_i и Х_j , нетрудно подсчитать, что коэффициент корреляции между Х_i и X_j равен ±1.

Таким образом, коэффициент корреляции  служит как бы оценкой бли­зости зависимости между случайными величинами к линейной.  Для неза­висимых случайных величин  коэффициент корреляции равен нулю.  Однак он может равняться нулю и для зависимых случайных величин.  Например, пусть случайные величины Х и Y связаны параболической зависимостью Y = Х²  , т.е. на плоскости (х,у) случайные величинны (X,Y) распределены вдоль параболы, и пусть распределение вероятностей величины Х симметрично относительно начала координат. Тогда Е(Х) = 0  и интеграл, выражающий коэффициент корреляции, окажется симметричным относитель­но оси у, а следовательно, обратится в нуль.

Случайные величины называются коррелированными, если их  корреляционныи момент не равен нулю, в противном случае они называются некоррелированными. Независимые случайные величины всегда не коррелирован Понятно, что в общем случае  корреляционный момент случайных величин X и Y равен нулю, когда совместное распределение этих случайных ве­личин Р(Х,Y) симметрично относительно хотя бы одной из прямых, парал лельных осям координат и проходящих через точку, определяющую их математические ожидания.

Итак, коэффициент корреляции не может служить характеристикой зани симости или независимости случайных величин. Равенство этого коэффи­циента нулю является лишь необходимым условием независимости, но не достаточным.  В следующей теореме  указывается необходимое и достатс ное условие независимости; правда, к сожалению, оно является мало пригодным для практической проверки.

Теорема 3.1.   Случайные величины Х и Y являются независимыми в том и только том случае, если для любых непрерывных функций  (на вещественной оси) f и, обращающихся в нуль вне конечного интер­вала,  имеет место равенство:

Е(f(Х)y(Y))  = Е(f(Х))·Е(y(Y)).

Доказательство. Необходимость очевидна: при независимости величин математическое ожидание, представляющее соббй интеграл от пары функ­ций, интегрируемых каждая по своей вероятностной мере, распадается на произведение интегралов.  При доказательстве достаточности следуе вспомнить, что , по определению, случайные величины называются неза­висимыми, если вероятность их совместной реализации равна произведению вероятностей каждой из них. Но из условия теоремы получаем что вероятность совместной реализации равна произведению вероятносте при fºyº1

Рассмотрим теперь вероятностные меры, функции распределения и математические ожидания на произвольных подмножествах конечномерног пространства и на произведении пространств. Приведенные ниже интег­ральные представления для случая плоскости понятным образом распрост раняются на многомерные пространства.

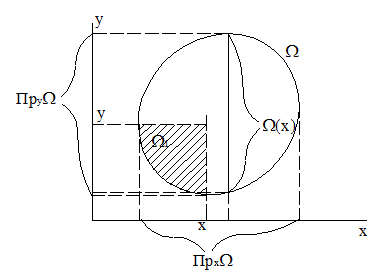
Пусть на множестве WÎR² координатные величины Х и Y являются случайными. Их распределение нa W задается  вероятностной мерой Р, определенной на s-алгебре подмножеств множества W. Вероятно­стная мера Р на множестве W,  может быть записана  в виде одного из следующих, равных  друг другу интегралов:

                              (3.1.)

где Пр_xW - проекция множества W на ось x, W(x) - сечение множества W  некоторой прямой  х=const.  Все пять введенных мер Р(х,у), Р₁(х), P₂(у), Р₁(х/у)  и  Р₂(у/х)  являются вероятностными мерами. Меры  Р₁(х)  и P₂(y) называются маргинальными (проекциями мер Р на оси  х  и у), а меры Р₁(х/у) и Р₂(у/х) - условными мерами. Соответствующие этим мерам функции распределения вероятностей называются соответственна маргинальными и условными распределениями. Нетрудно основываясь на одной из трех приведенных форм интегрального представ ления вероятности, определить функции распределения F(x)= P(X £ x) и F(у)= Р(У £ у)  или же функцию распределения F(х,у) = Р(Х £ х, Y £ у). Приведем, например, одно из возможных представле­ний для  функции распределения F(х,у):

           

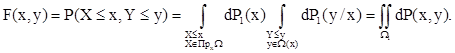
Область W1=WÇ (X£ x, Y£ Y )изображен на рис.

В приведенном подходе к анализу случайных величин Х и Y  исходным понятием y нас являлась область W на плоскости (х,у) с определенной на ее подмножествах вероятностью P. Однако весьма часто бывает и нао­борот: задаются независимые случайные величины Х и Y, каждое со свои собственным вероятностным распределением, т.е. исходными являются дв частных (маргинальных) распределения, а вероятности на плоскости (т.е. Р(х,у)) получаются из них с помощью произведений пространств. Рассмотрим два произвольных вероятностных (выборочных) пространства W₁ и W₂, на s-алгебрах U₁ и U₂ которых  определены вероятно­стные меры P₁ и Р₂, соответственно. Можно, в частности, принять W₁=R^m и W₂=Rⁿ. Пусть  А₁ - произвольное подмножество из W₁, принадлежащее s-алгебре U₁, а  А₂ - аналогичное подмножество W₂. На произведении пространств W₁´W₂ рассмотрим множества вида A₁´А_2. Множества такого вида будем наделять вероятностями по правилу умножения:

Р(A₁´А₂) = Р₁(A₁)·Р₂(А₂).

Известно, что на наименьшей s-алгебре, содержащей все множества типа A₁´А₂, существует единственная вероятностная мера Р, такая, что вероятности «прямоугольников» задаются  приведенным правилом умно­жения. Эта наименьшая s-алгебра обозначается U₁´U₂, а опреде­ленная на ней мера Р  называется произведением мер Р₁ и Р₂.

Понятно, что в рассмотренном выше случае, когда мы сначала опреде ляли вероятности Р(х,у) на произведении пространств (х,у), а затем уже вводили маргинальные распределения  Р₁(х) и Р₂(у), исходная s-алгебра U на (х,у) не могла быть меньше s-алгебры произведения.

В общем случае случайными величинами мы назвали выше не сами эле­менты s-алгебры U, а функции U, определенные на W  и измеримые от­носительно U (и, в частности, бэровские функции). В частном случае эти функции могут тождественно равняться единице; и тогда объектом исследования оказываются сами элементы s-алгебры - случайные вели­чины. Записанное выше равенство (3.1)  выражает собой частный случай теоремы Фубини о повторном интегрировании на произведении пространен когда рассматривается единичная функция. В более общем случае теорем Фубини утверждает существование повторных интегралов при выполнении весьма слабых требований к классу функций U(х,у), определенных на W (например, измеримых относительно алгебры-произведения) и к классу условных вероятностей (например, регулярных в определенном ниже смысле).Согласно этой теореме имеет место равенство (теорема умножения вероятностей):

Рекомендуем посмотреть лекцию "Подразделение паблик рилейшнз".

    

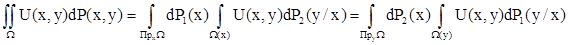
В отношении, например, первого из повторных интегралов в (3.2) регу­лярность  условной вероятности означает, что интеграл

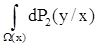
есть измеримая относительно s-алгебры U₁ функция от  х и  есть вероятносная мера  на s-алгебре U₂.

Понятно, что левая часть равенств (3.2) определяет в общем случае математическое ожидание случайной величины U(х,у), определенной на подмножестве W некоторого конечномерного пространства, а правые части определяют два возможных представления математического ожида­ния в виде повторных интегралов. Внутренние интегралы в каждом из повторных интегралов в (3.2) определяют условные математические ожи­дания.  Аналогичным образом строятся повторные интегралы на произве­дении более чем двух пространств.

Определенные проблемы возникают в связи с тем, что вероятности можно приписывать разным подмножествам выборочного пространства W. Наиболее широко распространенным подходом в теории вероятности явля­ется подход, при котором вероятности приписывают борелевским множествам U^b. Но возможны подходы, при которых s-алгебра является не первичным по отношению к вероятностной мере понятием, а вторичным, и некоторые из подобных подходов мы рассмотрим ниже. Некоторые из воз­никающих при этом проблем состояв в следующем. Например, в случае классического определения вероятностей на борелевских множествах U^b следует иметь в виду, что  любое борелевскюе множество ВÎU^b содержит неборелевские подмножества. Следовательно, множество борелевской меры нуль  может содержать подмножества, на которых вероятности не определены. Т.е. ситуация оказывается странной: мы имеем множества нулевой меры, подмножества которых, вообще говоря, никак не оценива­ются с точки зрения вероятности. Вообще говоря, эту неприятность не­трудно обойти, приняв,  что если  А Ì В и  Р{В}=0 , то  Р{А}=0. Подобное допущение требует расширения s-алгебры U^b до минимальной s-алгебры  U, содержащей U^b и все подмножества нулевых множеств. Подобное расширение называется лебеговским пополнением исходного ве­роятностного пространства. Множество А принадлежит пополненной s-алгебре U^b тогда и только тогда, когда  А-В  и  В-А  содержатся в нулевом множестве.  Лебеговское пополнение удобно в задачах, в ко­торых задано всего одно распределение Р. Если же вероятностных рас ределений  более одного, то возможны  неприятности, связанные с тем, что, например, пополненная s-алгебра U, построеннная с применением распределения Р₁, будет отличатьcя от пополненной s-алгебры,построенной с применением распределения Р₂ , а следовательно, величины, случайные по отношению к одной из этих алгебр, перестанут быть таковыми по отношению к дру­гой s-алгебре.