Мера Радона

Мера Радона

Определение. Семейство T подмножеств множества X образует его топологию, если оно содержит пустое множество, само X, сумму любого числа А_к и пересечение А_к конечного числа своих подмножеств. Топологическим пространством называется пара (Х, Т), т.е. X с заданной в нем топологией Т. Будем обозначать это пространство через Т.

Задать топологию в X – это значит указать те подмножества, которые считаются в X открытыми. Множества Т A, дополнительные к открытым, называются замкнутыми множествами топологического пространства Т. Поскольку X и пустое множество дополняют друг друга, то они одновременно открыты и замкнуты.

Пусть во множестве X заданы две топологии: Т₁ и Т₂. Топология Т₁ сильнее топологии Т₂ , если система множеств Т₁ содержит систему множеств Т₂, т.е. Т₁ Т₁.

Если заданы две системы окрестностей A₁ и A₂, то топология, определенная системой A₁, сильнее топологии, определенной системой A₂, тогда и только тогда, когда они различны и каждая окрестность A₂ содержит некоторую окрестность A₁.

Множество, открытое в слабой топологии, тем более открыто в сильной. В совокупность всех возможных топологий в X можно ввести частичную упорядоченность Т₁ Т₂ Т₃  ... Т. В этой последовательности есть максимальный элемент Т₁ – топология, в которой все множества открыты (например, в произвольном множестве X можно ввести топологию положив открытыми все его подмножества), и есть минимальный – топология Т, в которой открыты только X и пустое множество (например, в произвольном множестве X можно ввести топологию, считая открытыми только X и пустое множество: это пространство «слипшихся» точек, в котором замыкание каждого непустого множества есть все X).

Если учесть, что окрестностью точки x  Т называется всякое открытое множество A  Т, содержащее x, то из самого определения топологического пространства следует, что для того чтобы множество в Т было открытым, необходимо и достаточно, чтобы оно содержало некоторую окрестность каждой своей точки. Тогда, переходя к дополнениям в определении топологии, получаем, что сумма конечного числа замкнутых множеств замкнута и что пересечение любого числа замкнутых множеств замкнуто. Замыканием  множества A называется пересечение всех замкнутых множеств, содержащих A. Замыкание множества A состоит из изолированных точек этого множества, из предельных точек, не принадлежащих A. Напомним, что точка x  X называется предельной точкой множества A  X, если любая ее окрестность содержит бесконечно много точек из A, причем сама точка x может не принадлежать A. Точки из , не являющиеся внутренними для A, образуют границу множества A.

Можно определить топологическое пространство как множество, на котором задана операция замыкания. Тогда если в X заданы две топологии Т₁ и Т₂, то Т₁ сильнее Т₂ тогда и только тогда, когда замыкание всякого множества в топологии Т₁ содержится в его замыкании в топологии Т₂ .

Определение. Семейство 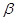 называется системой образующих топологии Т, если Т есть слабейшая из топологий, содержащих  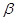( Т  ).

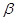Рекомендуемые материалы

Пересечение произвольного множества топологий Т’ = Т_к в X есть топология в X, которая является наиболее слабой среди топологий Т_к .

Если 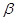 - произвольная система подмножеств множества X, то существует минимальная топология Т в X, содержащая  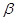(в этом случае  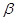является системой образующих топологий Т).

Обычно удобно задавать не совокупность всех открытых в X подмножеств, а некоторую определяющую систему подмножеств, по которой можно построить любое из заданных открытых множеств посредством операций, входящих в определение топологии. Например, на прямой открыты лишь те множества, которые могут быть представлены в виде суммы некоторого числа интервалов. Это приводит к определению базы или базиса топологического пространства.

Определение. Семейством 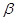 открытых подмножеств из X называется базой, или базисом топологического пространства Т, если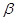 Т и всякое открытое множество из Т может быть представлено как сумма некоторого числа множеств из .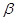

Теорема. Чтобы система 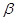открытых множеств { X_к } была базой топологического пространства Т, необходимо и достаточно, чтобы для каждого открытого множества A и каждой точки x  A нашлось бы такое множество X_к из этой системы, что x  X_к  A, т.е. чтобы любую точку из произвольного открытого множества A можно было окружить окрестностью X_к  A и X_к .

Определение. Если Y  X и Т – некоторая топология в X, то топология         Т_у = { A: A = B Y,  B  Т }          называется топологией пространства Y, индуцируемой топологией пространства X, или относительной топологией в Y.

Подмножество в Y называется относительно открытым, если оно открыто в топологии Т_у ; относительно замкнутым, если его дополнение в Y относительно открыто.

Топологию во множество X можно ввести многими способами. Один из них, наиболее плодотворный, основан на введении понятий метрики.

Определение. Пусть X – некоторое множество и - вещественная функция на произведении X * X, обладающая следующими свойствами:

1) (х, y)  0,      x, y  X ;

2) (х, y) = 0 в том и только том случае, если x = y ;

3) (х, y) = (у, x) ;

4) (х, y)  (х, z) +(z, y)  (неравенство треугольника).

Функция  называется метрикой или метрической функцией пространства X.

Метрическая топология в X – это слабейшая из топологий, содержащих сферы (шары) вида:  S ( x, a ) = { y /(х, y)  a }, где точка ч называется центром, а а – радиусом сферы. Метрическое пространство X оказывается топологическим пространством, если на базу окрестностей каждой точки x  X принять совокупность всех открытых шаров с центром в x. В этом случае говорят, что топология в X определена метрикой (х, y). Множество X с определенной в нем метрической топологией называется метрическим пространством.

Топологические пространства – это весьма общие пространства. В них могут встречаться ситуации, не имеющие места, например, в метрических пространствах. Например, в топологическом пространстве конечное множество точек может не быть замкнутым. В связи с этим представляет интерес выделить из топологических пространств такие, которые близки по свойствам к метрическим. Для этого надо не топологическое пространство наложить дополнительные ограничения. В качестве таких ограничений вводят, например, аксиомы отделимости:

Т₁) множество, состоящее из единственной точки, замкнуто;

Т₂) у любых двух несовпадающих точек x и у существуют непересекающиеся окрестности О_х и О_у ;

Т₃) для любого замкнутого множества A и произвольной точки x А существуют непересекающиеся окрестности;

Т₄) у любых двух непересекающихся замкнутых множеств A и В существуют непересекающиеся окрестности.

Топологическое пространство, обладающее свойствами Т₁) и Т₂), называется хаусдорфовым. В анализе редко встречаются пространства более общие, чем хаусдорфовы.

Топологическое пространство, обладающее свойствами Т₁) и Т₃), называется регулярным, а пространство, обладающее свойствами Т₁) и Т₄) называется нормальным. Почти все встречающиеся в анализе пространства являются нормальными. Всякое нормальное пространство регулярно, а регулярное хаусдорфово, но не наоборот.

Наиболее плодотворным для анализ оказались пространства, несколько более узкие, чем регулярные, но более широкие, чем нормальные, введенные А.Н.Тихоновым и получившие название вполне регулярных.

Определение вполне регулярного пространства основано на следующей аксиоме функциональной отделимости: два непересекающихся замкнутых множества A и В функционально отделимы в пространстве X, если существует определенная на всем X непрерывная функция 0  f(x)  1, равная нулю во всех точках множества A и равная единице во всех точках множества В.

Вполне регулярным называется функционально отделимое Т₁-пространство.

Особая роль вполне регулярных пространств проявляется в следующем. Урысоном было показано, что существуют регулярные пространства, на которых не существует каких-либо непрерывных функций, за исключением постоянных; в то же время незначительное усиление регулярных пространств до класса вполне регулярных позволило установить, что на любых вполне регулярных пространствах имеется достаточно много непрерывных функций. Еще одно замечательное свойство вполне регулярных пространств состоит в том, что они, наряду с хаусдорфовыми и регулярными, являются наследственными в том смысле, что любые из подмножества являются пространствами того же типа. Для нормальных пространств свойство наследственности удовлетворяется только в отношении замкнутых подмножеств (т.е. замкнутые подмножества нормального пространства нормальны).

Всякое метрическое пространство нормально (тем самым автоматически оно является и вполне регулярным, и регулярным, и хаусдорфовым). Урысон доказал, что непересекающиеся замкнутые множества в нормальном пространстве функционально отделимы.

Огромную роль в современной математике играет понятие компактности. Для его определения нам потребуется вспомогательное понятие покрытия. Покрытием множества A в топологическом пространстве Т называется семейство { A_К } открытых (или замкнутых) множеств, сумма которых содержит A, т.е. А_К  = A.

Если некоторая часть { A_Кi } покрытия { A_К } сама образует покрытие пространства Т, то { A_Кi } называется подпокрытием покрытия { A_К }.

Определение. Пространство Т называется компактным, если из всякого его покрытия можно выделить конечное подпокрытие.

Множество X  Т называется компактным, если оно, рассматриваемое как подпространство в Т, компактно.

Определение. Топологическое компактное хаусдорфово пространство называется компактом.

Компактны все замкнутые ограниченные подмножества конечномерного эвклидова пространства, сами же эти пространства не компактны.

В дальнейшем мы определим меры Радона как на компактном, так и на так называемом локально компактном пространстве. В связи с этим приведем определение локально компактного пространства.

Определение. Топологическое пространство Т называется локально компактным, если каждая его точка имеет окрестность, замыкание которой в Rⁿ локально компактно. Замкнутые подмножества локально компактного пространства также локально компактны. Закрытые подмножества локально компактного хаудсорфова пространства локально компактны.

Локально компактными пространствами являются замкнутые подмножества конечномерного эвклидова пространства; если же они ограничены, то компактны. (В R шар (0, y)  1 не компактен. Гильбертов кирпич – компакт в R).

Существуют топологические пространства, которые нельзя определить исходя из какой-либо метрики. Говорят, что топологическое пространство метризуемо, если существует метрика, порождающая его топологию. Большинство встречающихся в анализе пространств все же метризуемы. В конечномерном пространстве любые метрики эквивалентны, т.е. все метрики вводят одну и ту же топологию.

Рассмотрим теперь непрерывные отображения топологических пространств.

Отображение f топологического пространства X в топологическое пространство Y назовем непрерывным в точке x  X, если для любой окрестности В(у) точки y = f ( x ) найдется такая окрестность A(х) точки x, что f(A(x))  B(y). Отображение f : X  Y непрерывно, если оно непрерывно в каждой  точке x  X.

Теорема. Чтобы отображение f топологического пространства X в топологическое пространство Y было непрерывным, необходимо и достаточно, чтобы топология Т_x была не слабее топологии f ^–1(Т_y), или, что то же самое, чтобы прообраз f ^–1(B) всякого открытого множества B  Y был открыт в Х.

Теорема. Если X, Y и Z – топологические пространства и f и - непрерывные отображения X в Y и Y в Z соответственно, то отображение          z = (f(x)) пространства X в Z непрерывно.

Обратите внимание на лекцию "ЗОЩЕНКО Михаил Михайлович".

Определение. Гомеоморфизмом называется взаимно однозначное и взаимнонепрерывное отображение f : X Y, а топологические пространства X и Y называются гомеоморфными.

С топологической точки зрения гомеоморфные пространства эквивалентны: топологии в них служат образами и прообразами друг друга. При гомеоморфизме сохраняются свойства множества быть замкнутым, открытым или замыканием некоторого множества. Свойства, сохраняющиеся при гомеоморфизме, называют топологическими. Следует, однако, иметь в виду, что метрические свойства двух гомеоморфных между собой пространств могут быть различными, например, одно может быть полным, а другое – нет.

Рассмотрим один из естественных способов задания топологии на произведении пространств X и Y. Скажем, что множество E  X * Y открыто в топологии произведения Т_х* Т_y пространств X и Y, если вместе с любой своей точкой (a, b) оно содержит хотя бы одно произведение открытых множеств A*B, где A  Т_х , B  Т_y , a  A, b  B. Определенная таким образом топология Т_х* Т_y  называется произведением топологий, заданных на X и Y.

Топологию произведения можно задать также с помощью метрик. Например, если X и Y – метрические пространства с метриками ₁ и ₂ , то на произведении X * Y можно множеством способов задать метрики, в частности, положив:  = max (₁ ( x₁ , x₂), ₂ ( y₁ , y₂) ), или  = ₁ + ₂ , или                    = . Однако все эти метрики будут эквивалентны, т.е. будут определять одну и ту же топологию.

Пример пространства Т₁ , не являющегося хаусдорфовым, можно простроить, взяв множество X всех действительных чисел и любой нечисловой объект Y. В качестве открытых рассматриваются все открытые в X интервалы и представимые с помощью них открытые множества, а также все множества, получающиеся выбрасыванием из X Y конечного числа точек. Это будет Т₁-пространство, не удовлетворяющее аксиоме Т₂), поскольку окрестности O(y) и O(x), где x – любая точка из X, пересекаются: в самом деле, O(y) содержит все действительные числа, кроме конечного их числа, а O(x) – открытое подмножество в X, содержащее интервал.

Примером хаудсорфова пространства, не являющегося регулярным, может служить отрезок [0, 1], в котором окрестности всех точек, кроме точки 0, определяются обычным образом, а за окрестности нуля принимаются различные полуинтервалы вида [0, x), из которых выброшены точки типа 1/K (K = 1, 2, 3, ... ). Полученное пространство хаусдорфово. Последовательность    { 1/K } – замкнутое множество в [0, 1], но неотделимое от 0 непересекающимися окрестностями (поскольку любая окрестность [0, x] нуля пересекается с любой окрестностью множества точек { 1/K } ).