Линейные пространства
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Введение. Основные понятия и определения.
§1. Аксиоматика линейных пространств.
Определение. Линейным пространством L = {a,b,c,…} называется множество, относительно элементов которого определены операции сложения и умножения на число, причем результаты этих операций принадлежат этому же множеству (говорят, что L замкнуто относительно операций сложения и умножения на число): 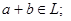
 .
.
(Элементы линейных пространств также будем называть векторами)
Для  эти операции удовлетворяют следующим условиям:
эти операции удовлетворяют следующим условиям:
1. a + b = b + a (коммутативность сложения).
2. (a + b) + c = a + (b + c) (ассоциативность сложения).
Рекомендуемые материалы
3. .
.
4. 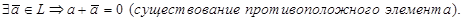
5. 1·а = а.
6. 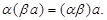
7. (α + β)а = αа + βа (дистрибутивность).
8. α(а + b) = αa + αb (дистрибутивность).
Перечисленные свойства, обычно, называют аксиомами. Имеют место теоремы:
Теорема 1. Нулевой элемент – единственен.
{От противного: 01,02; 01+02=01 и 02+01=02 (акс. (3)). Из акс.(1) следует: 01=02}
Теорема 2.  противоположный элемент – единственен.
противоположный элемент – единственен.
{Пусть для  }
}
Теорема 3. 0·а = 0.
{ }
}
Теорема 4. 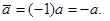
{ }
}
Примеры. 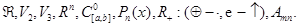
§2. Линейно зависимые и линейно независимые системы элементов.
Определение 1. Сумма  называется линейной комбинацией элементов а1, а2,…,аn с коэффициентами λk .
называется линейной комбинацией элементов а1, а2,…,аn с коэффициентами λk .
Определение 2. Система элементов линейного пространства {a1,…,an} называется линейно зависимой, если найдутся коэффициенты λ1,…,λn не все равные нулю, линейная комбинация с которыми равна нулю, т.е. 
Определение 3. Система элементов линейного пространства {a1,…,an} называется линейно
независимой, если ее линейная комбинация равна нулю только с нулевыми коэффициентами: 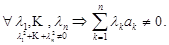
Имеют место несколько простых утверждений.
Теорема 1 (необходимое и достаточное условие линейной зависимости). a1,…,an – линейно зависима  когда хотя бы один из элементов является линейной комбинацией остальных.
когда хотя бы один из элементов является линейной комбинацией остальных.
{1.(необходимость: {ak} – л.з. ):  . Пусть, для определенности,
. Пусть, для определенности,  а1 – линейная комбинация остальных.
а1 – линейная комбинация остальных.
2.(достаточность: am – л.к.):  }
}
Теорема 2. Если один из элементов системы равен нулю, то вся система линейно зависима.
{ }
}
Теорема 3. Если подсистема линейно зависима, то и вся система линейно зависима.
{ }
}
Примеры.
1)  2)
2) 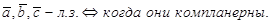
3) {f1 = 1, f2 = x, f3 = x2 } – линейно независимы.
§3. Базис. Размерность. Координаты.
Определение 1. Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
1) Система  линейно независима.
линейно независима.
2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов  ):
): 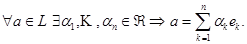
Примеры. Базис на плоскости (V2 – 2 неколлинеарных вектора), в пространстве (V3 – 3 некомпланарных вектора), в пространстве Rn (канонический базис), в пространстве многочленов степени ≤ n − (1,х,х2,…,хn).
Теорема 1. Коэффициенты разложения по базису – единственны.
{Пусть  }
}
Определение 2. Координатами элемента линейного пространства в некотором базисе называются коэффициенты разложения по этому базису.
(В силу Т.1 это определение корректно)
Будем писать:  .
.
В дальнейшем, по умолчанию, будем считать вектор вектором – столбцом, в противном случае будем писать строку координат в явном виде:  либо как
либо как 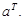
Теорема 2. При сложении векторов их координаты складываются: 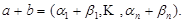
{ }
}
Теорема 3. При умножении вектора на число его координаты умножаются на это число:
λа = (λα1,…,λαn). { }
}
Определение 3. Размерностью линейного пространства L (обозначается dimL) называется максимальное число линейно независимых элементов этого пространства.
Если такого числа не существует – пространство называется бесконечномерным.
Теорема 4. Размерность линейного пространства равна числу базисных векторов. {б/д}
Отсюда, в частности, следует, что все базисы одного пространства состоят из одинакового числа векторов.
Примеры. V2 ; V3 ; Rn.
§4. Подпространства линейных пространств. Линейные оболочки.
Определение 1. Подпространством линейного пространства L называется такое подмножество
элементов L, которое само является линейным пространством.
Т.е. подпространство замкнуто относительно операций сложения и умножения на число и содержит нулевой элемент. (Все аксиомы выполняются автоматически).
Примеры.  , множество решений однородной СЛАУ.
, множество решений однородной СЛАУ.
Определение 2. Рангом системы векторов  называется максимальное число линейно независимых векторов этой системы. Обозначают: rang
называется максимальное число линейно независимых векторов этой системы. Обозначают: rang .
.
Определение 3. Линейной оболочкой системы элементов , принадлежащих L , называется совокупность всех линейных комбинаций этих элементов (иногда говорят линейная оболочка, натянутая на систему векторов):
, принадлежащих L , называется совокупность всех линейных комбинаций этих элементов (иногда говорят линейная оболочка, натянутая на систему векторов):  .
.
Непосредственно из определения следует, что любая линейная оболочка является линейным пространством, а любое линейное пространство – линейной оболочкой натянутой на какой-либо базис этого пространства.
Теорема 1. (Основное свойство линейных оболочек). Любой вектор системы  , линейно зависящий от остальных, можно исключить без изменения линейной оболочки.
, линейно зависящий от остальных, можно исключить без изменения линейной оболочки.
{Пусть, для определенности,  а
а  произвольный . Тогда
произвольный . Тогда
 , т.е.
, т.е.  }
}
Следствие. Размерность линейной оболочки равна рангу соответствующей системы элементов:
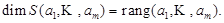
Глава 1. Теория матриц и системы линейных алгебраических уравнений (СЛАУ).
§1. Матрицы. Основные определения.
Определение 1. Матрицей называется прямоугольная таблица чисел.
Матрицу, состоящую из m строк и n столбцов, будем обозначать  , а числа m и n называть ее размерами. Числа, составляющие матрицу, называют ее элементами. Элемент матрицы, стоящий в i−той строке и j−ом столбце обозначается
, а числа m и n называть ее размерами. Числа, составляющие матрицу, называют ее элементами. Элемент матрицы, стоящий в i−той строке и j−ом столбце обозначается  (первый индекс – номер строки, второй – столбца). Таким образом:
(первый индекс – номер строки, второй – столбца). Таким образом:
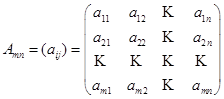
Определение 2. Матрица, все элементы которой – нули, называется нулевой матрицей.
Определение 3. Две матрицы называются равными, если их размеры совпадают и все
соответственные элементы попарно равны:  .
.
Определение 4. Матрица, все строки которой равны соответствующим столбцам матрицы А
(при этом, естественно, ее столбцы будут равны строкам А), называется транспонированной к А
и обозначается АТ.
Из определения сразу следуют несколько элементарных свойств:
1. Если  .
.
2.  .
.
3.  .
.
Определение 5. Матрица, у которой количество строк равно количеству столбцов (m = n)
называется квадратной и обозначается An .
Совокупность элементов квадратной матрицы  называется главной диагональю.
называется главной диагональю.
Квадратная матрица, все элементы которой ниже (выше) главной диагонали равны нулю, называется верхней треугольной (нижней треугольной) матрицей.
Определение 6. Квадратная матрица, все элементы которой вне главной диагонали равны нулю ( ), называется диагональной матрицей.
), называется диагональной матрицей.
Диагональная матрица с единичными элементами называется единичной матрицей.
Единичную матрицу будем обозначать буквой Е:  .
.
Определение 7. Квадратная матрица называется симметричной, если АТ = А, т.е. aij = aji.
§2. Простейшие операции над матрицами и их свойства.
1. Сложение (вычитание) матриц.
Суммой (разностью) двух матриц называется матрица, каждый элемент которой равен сумме (разности) соответствующих элементов слагаемых: 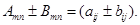
Из определения сразу следует, что складывать (вычитать) можно только матрицы одинаковой размерности.
2. Умножение матрицы на число.
Произведением матрицы на число называется матрица, каждый элемент которой равен произведению элемента исходной матрицы на это число: 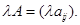
3. Произведение матриц.
Произведением матриц  называется матрица
называется матрица  , каждый элемент которой cij равен сумме попарных произведений элементов i– ой строки матрицы А на элементы j – го столбца матрицы В:
, каждый элемент которой cij равен сумме попарных произведений элементов i– ой строки матрицы А на элементы j – го столбца матрицы В: 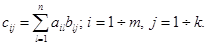
Пример. 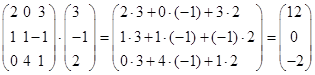
Замечания. 1) Умножать матрицы можно только в том случае, когда число строк правой матрицы равно числу столбцов левой. Отсюда следует, что при умножении не квадратных матриц, их нельзя менять местами по определению.
2) В случае умножения квадратных матриц, произведение, вообще говоря, зависит от порядка сомножителей (т.е. произведение матриц не коммутативно).
3) Полезно заметить, что формула для вычисления элемента произведения совпадает с формулой вычисления скалярного произведения векторов в декартовой системе координат.
Определение. Если произведение двух квадратных матриц не зависит от порядка сомножителей
(т.е. АВ = ВА), то эти матрицы называются перестановочными между собой.
Свойства арифметических операций.
- А +В = В + А
- А + (В + С) = (А + В) + С
![]()
![]()
- А(ВС) = (АВ)С
- А(В +С) = АВ + АС
- (А + В)С = АС + ВС
- АЕ = ЕА = А
{Первые 4 свойства очевидны. Докажем одно из последующих, например, св – во 6:
 }
}
Из двух первых операций (т.е. линейных операций) и их свойств (св. 1 – 4) следует, что матрицы одинаковой размерности образуют линейное пространство. Доказать самостоятельно, что dimL(Amn) = m×n , приведя пример базиса этого пространства.
Свойства арифметических операций для транспонированных матриц.
1)  . 2)
. 2)  . 3)
. 3)  . {Слева – строки А на столбцы В и транспонирование. Справа – столбцы В на строки А , т.е. уже транспонированная.}
. {Слева – строки А на столбцы В и транспонирование. Справа – столбцы В на строки А , т.е. уже транспонированная.}
§3. Определитель квадратной матрицы и его свойства.
Одной из важнейших характеристик квадратных матриц является ее определитель или детерминант:  . Дадим рекуррентное определение этого понятия.
. Дадим рекуррентное определение этого понятия.
1) Определитель второго порядка равен: 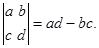
2) Определитель третьего порядка вычисляется по формуле

Таким образом, вычисление определителя третьего порядка свелось к вычислению трех определителей второго порядка. Каждый из них получается вычеркиванием строки и столбца, которые содержат элемент, стоящий перед этим определителем. Знаки перед слагаемыми вычисляются по формуле  , где i и j − индексы этого элемента. Данная формула называется разложением определителя по первой строке. Определитель четвертого порядка выражается по этому же правилу через определители третьего порядка и так далее.
, где i и j − индексы этого элемента. Данная формула называется разложением определителя по первой строке. Определитель четвертого порядка выражается по этому же правилу через определители третьего порядка и так далее.
Утверждение. Определитель может быть разложен по любой строке или столбцу {б/д}.
Перечислим без доказательства основные свойства определителей.
- Столбцы и строки определителя равноправны. Следствие:
![]()
- Определитель, содержащий нулевую строку (столбец), равен нулю.
- Постоянный сомножитель любой строки (столбца) можно вынести за знак определителя.
- Если к любой строке (столбцу) определителя прибавить любую другую строку (столбец), умноженную на произвольное число, то определитель не изменится.
- Если одна из строк (столбцов) линейно выражается через остальные, то определитель
равен нулю.
- Если поменять местами две строки (столбца), то определитель изменит знак.
- det(E) = 1.
![]() (определитель произведения равен произведению определителей)
(определитель произведения равен произведению определителей)- Определитель диагональной и треугольных матриц равен произведению диагональных элементов.
Определение. Матрица, определитель которой равен нулю, называется вырожденной.
§4. Миноры и ранг матрицы.
Рассмотрим матрицу  . Выберем k произвольных строк и k произвольных столбцов этой матрицы (
. Выберем k произвольных строк и k произвольных столбцов этой матрицы ( ).
).
Определение 1. Минором k – го порядка матрицы А (обозначается Мk) называется определитель, составленный из элементов, стоящих на пересечении выбранных k строк и столбцов матрицы А.
Определение 2. Рангом матрицы А (rang(A)) называется максимальный порядок минора, отличного от нуля. Т.е., rang(A) = r, если 1)  , 2)
, 2)  Любой минор,
Любой минор,
имеющий порядок r, называется базисным минором матрицы А. (Из определения сразу следует, что  )
)
Строки и столбцы матрицы А, на которых строится базисный минор, так же называются базисными.
Имеет место очень важное утверждение:
Теорема о базисном миноре. Любая строка (столбец) матрицы А является линейной комбинацией базисных строк (столбцов). {б/д}
Любую матрицу  можно рассматривать как упорядоченную систему из m n – мерных или n m – мерных векторов. Теорема о базисном миноре позволяет доказать следующую фундаментальную теорему:
можно рассматривать как упорядоченную систему из m n – мерных или n m – мерных векторов. Теорема о базисном миноре позволяет доказать следующую фундаментальную теорему:
Теорема 1. Ранг матрицы равен рангу системы векторов, составляющих эту матрицу.
{Для определенности рассмотрим систему строк матрицы (S). Выберем произвольный
базисный минор Mr . По предыдущей теореме любая строка матрицы, не принадлежащая
базисным, линейно выражается через базисные. Следовательно, ее можно исключить из
системы не изменив ранг самой системы (Введение, §4, Т.1). Отсюда получаем, что
rang(S) ≤ r. Но, если ранг будет строго меньше r, то одна из строк базисного минора будет линейной комбинацией остальных и Mr = 0 (§3,св.5), что противоречит условию. Таким образом – rang(S) = rang(A)}
Следствием Т.1 для квадратных матриц является обобщение свойства 5 §3:
Теорема 2. Определитель матрицы равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.
{Необходимость. Пусть det(An) = 0  r < n
r < n  одна из строк – линейная комбинация остальных
одна из строк – линейная комбинация остальных  строки линейно зависимы.
строки линейно зависимы.
Достаточность. Строки линейно зависимы  одна из строк – линейная комбинация остальных. По свойству 5§3 det(An) = 0 (Вычтем эту линейную комбинацию из рассмотренной строки и получим определитель с нулевой строкой)}
одна из строк – линейная комбинация остальных. По свойству 5§3 det(An) = 0 (Вычтем эту линейную комбинацию из рассмотренной строки и получим определитель с нулевой строкой)}
§5. Вычисление ранга матрицы.
Для вычисления ранга матрицы используется два метода.
I. Метод окаймляющих миноров.
Определение 1. Окаймляющими минорами некоторого фиксированного минора называются все миноры, полученные добавлением к нему дополнительного столбца и дополнительного строки данной матрицы ( ).
).
Метод заключается в отыскании произвольного отличного от нуля минора и вычисления всех миноров, его окаймляющих. Если все эти миноры равны нулю, то ранг матрицы равен рангу исходного минора. В противном случае операция повторяется. Обоснованием метода служит
Теорема 1. rang(A) = r, если  {б/д}
{б/д}
II. Метод элементарных преобразований.
Определение 2. Элементарными преобразованиями называются следующие:
1. Перестановка двух строк (столбцов).
2. Умножение строки (столбца) на число, отличное от нуля.
3. Прибавление к одной строке (столбцу) другой строки (столбца), умноженной на число.
Теорема 2. Элементарные преобразования не меняют ранг матрицы.
{При указанных преобразованиях любой минор матрицы (как обычный определитель) может изменить свое значение только следующим образом: }
}
Определение 3. Матрица В, полученная из А элементарными преобразованиями, называется
эквивалентной А ( ).
).
Определение 4. Первый ненулевой элемент строки будем называть отмеченным.
Определение 5. Матрица называется ступенчатой, если отмеченный элемент каждой строки
расположен правее отмеченного элемента предыдущей.
Теорема 3. Любая матрица приводится к ступенчатому виду элементарными преобразованиями.
{Доказательство носит конструктивный характер и будет продемонстрировано на примере}
Пример. Привести матрицу к ступенчатому виду.
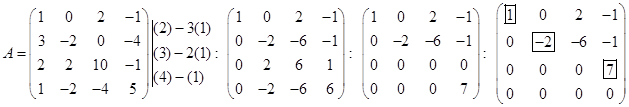
(в рамках −отмеченные элементы матрицы) Алгоритм может быть применен к любой матрице.
Теорема 4. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
{Снова продемонстрируем на том же примере: rang(A) = 3; в качестве базисного минора возьмем
минор, составленный из строк 1,2,3 и столбцов 1,2,4: }
}
§6. Обратная матрица.
Для квадратной матрицы важную роль играет понятие обратной матрицы.
Определение 1. Матрицей, обратной матрице А (обозначается  ), называется матрица, удовлетворяющая условию:
), называется матрица, удовлетворяющая условию:  .
.
Теорема 1. Обратная матрица (если она существует) − единственна.
{Пусть у матрицы А есть 2 обратных: В и С. Рассмотрим произведение ВАС:
ВАС = (ВА)С = ЕС = С. С другой стороны ВАС = В(АС) = ВЕ = В. Отсюда В = С}
Для вычисления обратной матрицы необходимо ввести еще несколько понятий.
Легко заметить, что минор (n – 1) − го порядка у квадратной матрицы Аn можно определять, не задавая строки и столбцы, а, указав один элемент  , вычеркнуть i−ю строку и j−ый столбец, на пересечении которых он находится. Поэтому минор Мп−1 матрицы Ап обычно обозначают
, вычеркнуть i−ю строку и j−ый столбец, на пересечении которых он находится. Поэтому минор Мп−1 матрицы Ап обычно обозначают  .
.
Определение 2. Алгебраическим дополнением элемента  называется величина
называется величина  .
.
Из определения детерминанта матрицы An сразу следует, что определитель матрицы равен сумме произведений элементов любой строки (столбца) на алгебраические дополнения этой строки (столбца):  ………………………………………….(*)
………………………………………….(*)
С другой стороны,  …………….(**)
…………….(**)
Т.е. сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю. {Фактически, мы получаем определитель с двумя одинаковыми строками (столбцами)}
Определение 3. Транспонированная матрица из алгебраических дополнений называется присоединенной матрицей: .
.
Теорема 2. 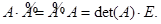
{При умножении k −ой строки А на k − ый столбец  получается det(A) (*), при умножении на любой другой столбец
получается det(A) (*), при умножении на любой другой столбец  получается ноль (**) }
получается ноль (**) }
Следствие. 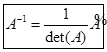
Пример. Найти обратную матрицу для  . {
. {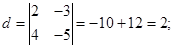
 .(проверка)}
.(проверка)}
Замечания. 1. Полезно запомнить, что обратная матрица второго порядка получается из исходной следующим образом: элементы главной диагонали меняются местами, у элементов второй диагонали изменяется знак. Полученная матрица делится на определитель.
2. Обратная матрица может быть получена с помощью элементарных преобразований. Для этого составляется матрица  и левая часть элементарными преобразованиями приводится к единичной. При этом матрица Е преобразуется в обратную {б/д}. Последний пример:
и левая часть элементарными преобразованиями приводится к единичной. При этом матрица Е преобразуется в обратную {б/д}. Последний пример:
 ;
; .
.
Свойства обратной матрицы.
1.  {
{ (св.7,8 §3)
(св.7,8 §3) 
 }
}
2. 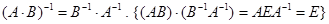
3.  {Из определения
{Из определения  следует, что А и
следует, что А и  − взаимно обратные матрицы.}
− взаимно обратные матрицы.}
В заключение докажем критерий существования обратной матрицы:
Теорема 3. Обратная матрица  существует тогда и только тогда, когда А − невырожденная матрица, т.е.
существует тогда и только тогда, когда А − невырожденная матрица, т.е. 
{1. Пусть  существует. Т.к. она равна присоединенной матрице, деленной на определитель, то последний не равен нулю. 2. Пусть
существует. Т.к. она равна присоединенной матрице, деленной на определитель, то последний не равен нулю. 2. Пусть  По Сл.Т.2 обратную матрицу можно вычислить.}
По Сл.Т.2 обратную матрицу можно вычислить.}
§7. Решение матричных уравнений.
Использование обратных матриц позволяет решать простые матричные уравнения относительно квадратных матриц. Рассмотрим пример одной из таких задач. Решить уравнение AXB + C = D, где  − неизвестная матрица.
− неизвестная матрица.
Матрица Х равна:  Пользуясь замечанием 1 предыдущего параграфа, имеем:
Пользуясь замечанием 1 предыдущего параграфа, имеем:
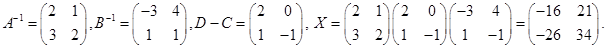
Замечание. Так как умножение матриц не коммутативно, необходимо внимательно смотреть за тем, с какой стороны следует умножать правую часть на обратные матрицы.
§8. Системы линейных алгебраических уравнений (СЛАУ).
Определение 1. Система уравнений  называется системой m
называется системой m
линейных алгебраических уравнений с n неизвестными (сокращенно СЛАУ).
Такая запись уравнений носит название координатной формы записи.
Более компактной записью является матричная форма. Нетрудно видеть, что левая часть системы представляет собой вектор, полученный умножением матрицы системы  на вектор
на вектор
неизвестных  . В правой части получается вектор правых частей
. В правой части получается вектор правых частей  (оба вектора – столбцы). Использование этой закономерности позволяет записывать системы в более компактном виде:
(оба вектора – столбцы). Использование этой закономерности позволяет записывать системы в более компактном виде:
 − матричная форма записи. В случае невырожденной квадратной матрицы решение
− матричная форма записи. В случае невырожденной квадратной матрицы решение
системы может быть записано в виде 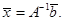
Рассмотрим еще несколько общих понятий, относящихся к СЛАУ.
Определение 2. СЛАУ называется совместной, если у нее существует хотя бы одно решение.
Если решений не существует, система называется несовместной.
Определение 3. СЛАУ, вектор правых частей которой равен нулю:  = 0, называется
= 0, называется
однородной. В противном случае система называется неоднородной.
Для однородных СЛАУ имеют место несколько общих утверждений.
Теорема 1. Однородная СЛАУ всегда совместна.
{Нулевой вектор всегда является решением однородной СЛАУ}
Теорема 2. Множество решений однородной СЛАУ образует линейное пространство.
{Пусть  − решения системы
− решения системы  , т.е. их линейная комбинация тоже решение. Выполнение аксиом − очевидно.}
, т.е. их линейная комбинация тоже решение. Выполнение аксиом − очевидно.}
Замечание. Пространство решений однородной СЛАУ является, очевидно, подпространством линейного пространства n – мерных векторов  .
.
§9. Квадратные СЛАУ. Правило Крамера.
Рассмотрим вначале СЛАУ с квадратной матрицей А − число уравнений равно числу неизвестных: 
Правило Крамера.
Обозначим определитель матрицы буквой d , а определители матриц, полученных из А заменой k – го столбца столбцом правых частей  через dk .
через dk .
Теорема (правило Крамера). Если определитель матрицы системы  , то система имеет единственное решение, которое может быть получено по формулам:
, то система имеет единственное решение, которое может быть получено по формулам: 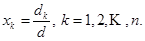
{ – аналогично. Единственность − от противного.}
– аналогично. Единственность − от противного.}
§10. Критерий совместности СЛАУ. Теорема Кронекера – Капелли.
Вернемся к общим СЛАУ  . Введем еще одно понятие.
. Введем еще одно понятие.
Определение. Матрица, составленная из коэффициентов при неизвестных и столбца правых частей, называется расширенной матрицей системы:  .
.
Теорема (Кронекера – Капелли). СЛАУ совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу исходной матрицы системы, т.е.  .
.
{1. Система совместна. Правая часть есть линейная комбинация столбцов матрицы, коэффициенты которой равны координатам вектора решения. Т.е.  .
.
2.  . Следовательно, в качестве базисного минора расширенной матрицы можно взять базисный минор матрицы А. По теореме о базисном миноре (§4) правые части равны линейной комбинации базисных столбцов матрицы. В качестве решения можно взять коэффициенты этой линейной комбинации.}
. Следовательно, в качестве базисного минора расширенной матрицы можно взять базисный минор матрицы А. По теореме о базисном миноре (§4) правые части равны линейной комбинации базисных столбцов матрицы. В качестве решения можно взять коэффициенты этой линейной комбинации.}
§11. Общее решение СЛАУ.
Определение. Множество решений системы линейных алгебраических уравнений 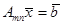
называется общим решением этой системы. Т.е. любой вектор этого множества есть решение и любое решение этой системы принадлежит указанному множеству.
Из §8 следует, что общим решением однородной системы является некоторое подпространство пространства  . Для неоднородной системы это не так: общее решение неоднородной системы не образует линейного пространства.
. Для неоднородной системы это не так: общее решение неоднородной системы не образует линейного пространства.
{Нулевой вектор (0,0,…,0) не является решением исходной системы.}
Итак, дана совместная система 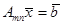 , матрица которой имеет ранг равный r. Для простоты будем считать, что базисный минор матрицы находится в левом верхнем углу (этого всегда можно добиться перестановкой строк и изменением нумерации неизвестных). Оставим первые r уравнений системы и перенесем неизвестные
, матрица которой имеет ранг равный r. Для простоты будем считать, что базисный минор матрицы находится в левом верхнем углу (этого всегда можно добиться перестановкой строк и изменением нумерации неизвестных). Оставим первые r уравнений системы и перенесем неизвестные  в правую часть. Если теперь дать этим неизвестным произвольные фиксированные значения, то по Т. Крамера полученная система будет иметь единственное решение (определитель системы = базисному минору ≠ 0). Это решение (вместе с
в правую часть. Если теперь дать этим неизвестным произвольные фиксированные значения, то по Т. Крамера полученная система будет иметь единственное решение (определитель системы = базисному минору ≠ 0). Это решение (вместе с  ) является решением исходной системы, так как все строки расширенной матрицы (по критерию Кр. – К. ) есть линейные комбинации базисных.
) является решением исходной системы, так как все строки расширенной матрицы (по критерию Кр. – К. ) есть линейные комбинации базисных.
Можно показать, что любое решение может быть получено таким же образом. Достаточно взять  из предложенного решения и первые неизвестные определятся однозначно по теореме Крамера. Тем самым, указанный метод позволяет получить общее решение системы.
из предложенного решения и первые неизвестные определятся однозначно по теореме Крамера. Тем самым, указанный метод позволяет получить общее решение системы.
В общем случае базисного минора будем называть неизвестные, не входящие в базисный минор, свободными, а, входящие в него – зависимыми.
На практике матрицу системы сначала приводят к ступенчатому виду, затем выбирают базисный минор и , таким образом, зависимые и свободные неизвестные. При этом, желательно все преобразования производить только со строками, чтобы сохранить нумерацию неизвестных. После этого зависимые переменные выражают через свободные и записывают общее решение.
Рассмотрим на примере данный алгоритм и сделаем несколько общих выводов.

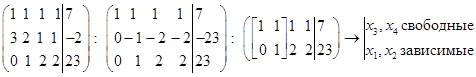
Пусть  .
.
 Последняя формула, вообще говоря, дает общее решение данной системы при произвольных значениях с3 и с4 . Более удобной является векторная форма записи:
Последняя формула, вообще говоря, дает общее решение данной системы при произвольных значениях с3 и с4 . Более удобной является векторная форма записи:
 .
.
Из этого примера можно вывести несколько важных общих закономерностей.
I. Ранг системы решений (S(x)) равен числу свободных неизвестных, т.е. rang(S(x)) = n – r, где
n – количество неизвестных, а r – ранг матрицы системы (В примере: n = 4, r = 2, rang(S) = 2).
Обычно, свободные неизвестные для каждого из решений выбираются следующим образом
(для простоты будем считать  зависимыми, а
зависимыми, а  − свободными):
− свободными):
для решения 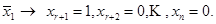
для решения 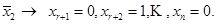
…………………………………………………
для решения 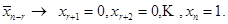
Вместе с этой лекцией читают "Работы Анри Файоля по научному управлению".
Легко видеть, что полученные решения 1) линейно независимы и 2) любое решение системы будет их линейной комбинацией.
II. Вектор  является частным решением неоднородной системы при с3 = с4 = 0, а векторы
является частным решением неоднородной системы при с3 = с4 = 0, а векторы  линейно независимыми решениями соответствующей однородной системы уравнений. Совокупность линейных комбинаций векторов
линейно независимыми решениями соответствующей однородной системы уравнений. Совокупность линейных комбинаций векторов 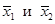
описывает всю линейную оболочку решений однородной системы, т. е. − общее решение однородной системы уравнений.
III. Общее решение неоднородной системы равно сумме общего решения однородной системы
и частного решения неоднородной:
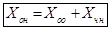

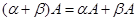
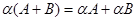
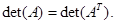
 (определитель произведения равен произведению определителей)
(определитель произведения равен произведению определителей)
















