Вероятностное пространство

Вероятностное пространство

Первые теоретические результаты по теории вероятностей относятся

к середине 17 века и принадлежат Б.Паскалю, П.Ферма, Х.Гюйгенсу, Я.Бернулли. Своим успехам в 18 веке и начале 19 века эта теория обязана А.Муавру, П.Лапласу, К.Гауссу, С.Пуассону, А.Лежандру. Значительные успехи в теории вероятностей были достигнуты в конце 19 и начале 20 века в работах Л.Больцмана, П.Чебышева, А.Ляпунова, А.Маркова, Э.Бореля и др. Однако, даже к началу 20 века еще не бы­ло создано строгой и непротиворечивой теории. Только аксиоматический подход позволил достичь этого. Впервые аксиоматическое построение теории было сделано С.Н.Бернштейном в 1917г., который в основу сво­их построений положил сравнение случайных событий по степени их вероятности. Однако этот  подход не получил дальнейшего развития. Более плодотворным оказался аксиоматический подход, основанный на теории множеств и теории меры, развитый А.Н.Колмогоровым в 20-х годах 20-го века. j аксиоматике Колмогорова понятие случайного события, в отличие от классического подхода, не является исходным, а является следст­вием более элементарных понятий. Исходным у Колмогорова является множество (пространство) W элементарных событий (пространство ис­ходов, выборочное пространство). Природа элементов этого простран­ства не играет роли.

Если А,В,С Î W , то очевидны следующие отношения, установленные в теории множеств:

А+А = А, АА = А,  АÆ =Æ , А +Æ = A, A +W =W, AW = А, W = Æ, Æ = W, А=А,

где чертой сверху обозначено дополнение в W; А+В = А B, AB = А + В, АВ=ВА, А+В = В+А, (А+В)+С=А+(В+С), (АВ)С=А(ВС), А(В+С) = АВ+АС, А+ВС = (А+В)(А+С);

здесь Æ обозначает пустое множество, т.е. невозможное событие.

В аксиоматике Колмогорова рассматривается некоторая система U подмножеств множества W, элементы которой называются случайными событиями. Система U удовлетворяет следующим требованиям: если под­множества А и В множества W входят в систему U, то эта система содержит также и множества А È В, А Ç В, А и В ; само множество W. также является элементом системы U. Подобная система множеств на­зывается (булевой) алгеброй множеств.

Очевидно, из определения алгебры множеств следует, что семейству U принадлежит также и пустое множество Æ. Таким образом, алгебра множеств (т.е. множество случайных событий) замкнута  относительно операций сложения, пересечения и образования дополнений, а следова­тельно, элементарные операции над случайными событиями не выводят за пределы множества случайных событий U.

Рекомендуемые материалы

Для большинства приложений необходимо требовать, чтобы семейство множеств U включало в себя не только конечные суммы и пересечения подмножеств множества W, но и счетные суммы и пересечения. Это приводит нас к определению понятия s-алгебры.

Определение 1.1. s-алгеброй называется семейство подмножеств  (U) множества W, замкнутое относительно операций образования допол­нений, счетных сумм и счетных пересечений.

Понятно, что любая s-алгебра содержит само множество W и пустое множество. Если задано произвольное семейство U подмножеств множества W то наименьшая s-алгебра, содержащая все мно­жества семейства U, называется s-алгеброй, порожденной семейст­вом U.

Наибольшая s-алгебра содержит все подмножества s; она полезна в дискретных пространствах W, в которых вероятность обычно определяют для всех подмножеств множества W. Однако в более общих про­странствах определить вероятность (определение вероятности будет дано ниже)  для всех подмножеств или невозможно, или нежелательно.  Другим крайним определением s-алгебры может служить s-алгебра, состоящая только из множества W. и пустого множества Æ.

В качестве примера выбора W и s-алгебры подмножеств U рас­смотрим игру, в которой участники бросают игральную кость, на каждой из шести граней которой нанесены цифры от 1 до 6.  При любых броса­ниях кости реализуется только шесть состояний: w₁, w₂, w₃, w₄, w₅ и w₆, i-ое из которых означает выпадение i очков. Семейство U случайных событий состоит из 2⁶ = 64 элементов, состав­ленных из всевозможных комбинаций w_i : w₁,…,w₆; (w₁,w₆),...,(w₅,w₆);(w₁,w₂,w₃),...,(w₁,w₂,w₃,w₄,w₅,w₆) Æ.

Случайные события, т.е. элементы s-алгебры U мы будем часто обозначать буквами А, В,… Если два случайных события А и В не имеют в своем составе одних и тех же элементов w_iÎW, то будем на­зывать их несовместимыми. События А и A называются противоположными (в других обозначениях, вместо A можно положить СА). Теперь можно перейти к определению понятия вероятности.

Определение 1.2. Вероятностной мерой Р на s-алгебре U подмноже­ств множества W  называется функция множества P, удовлетворяющая следующим требованиям:

1) Р(А) ³ 0;  AÎU;

2) P(W) = 1,

, т.е. обладающая свойством счетной аддитивности, где А_k- взаимно непересекающиеся множества из U.

Таким образом, каково бы ни было выборочное пространство W , вероятности мы приписываем только множествам  некоторой s-алгебры U и эти вероятности  определяются величиной меры Р на этих множествах.

Таким образом, в любой задаче на исследование случайных событий исходным понятием служит выборочное пространство s, в котором тем или иным образом выбирается s-алгебра , на которой уже  определяется вероятностная мера  Р . Следовательно, можно дать следующее определение

Определение 1.3.  Вероятностным пространством называется тройка (W,U,Р), состоящая из выборочного пространства W,s-ал­гебры U его подмножеств и вероятностной меры Р, определенной на U.

На практике могут встречаться задачи, в которых одним и тем же случайным событиям из U приписываются разные вероятности. Например, в случае симметричной игральной кости естественно положить:

Р(w₁) = Р(w₂) = ... = P(w₆) == 1/6,

а если кость несимметрична, то  более соответствующими реальности .могут оказаться следующие вероятности: P(w₁) = Р(w₂) = Р(w₃) = Р(w₄) = 1/4, Р(w₅) = Р(w₆)  = 1/12.

В основном мы будем иметь дело с множествами W, являющимися подмножествами конечномерного евклидова пространства  Rⁿ . Главным объектом теории вероятностей являются случайные величины, т.е. неко­торые функции, определенные на выборочном пространстве W. Наша первая задача - ограничить класс Функций, которыми мы будем опериро­вать. Желательно выбрать такой класс функций, стандартные операции над которыми не выводили бы из этого класса, в частности, чтобы из этого класса не выводили, например, операции взятия поточечных пре­делов, композиции функций и т.п.

Определение 1.4. Наименьший класс функций B, замкнутый относительно поточечных предельных переходов (т.е. если ¦₁,¦₂,... принадлежат классу B и при всех x существует предел ¦(x) = lim¦_n(x), то и ¦(x) принадлежит B), содержащий все непрерывные функции, назы­вается классом Бэра.

Из этого определения следует, что сумма, разность, произведение, проекция, композиция двух бэровских функций снова являются бэровскими функциями, т.е. всякая функция от бэровской функции снова есть бэровская функция. Оказывается, что если ограничиться более узкими классами функций, то никакого усиления или упрощения теории получить не удается.

В общем случае случайные величины, т.е. функции  Х = U(х), где XÎWÌRⁿ, следует определить так, чтобы события {X £ t} при лю­бом t имели определенную вероятность, т.е. чтобы множества {X £ t} принадлежали семейству U , для элементов которого определены веро­ятности Р, т.е. чтобы величины Р{X £ t} были определены. Это при­водит нас к следующему определению измеримости функции относительно семейства U.

Определение 1.5. Действительная функция  U(х),  xÎW, назы­вается U-измеримой, если для всякого действительного t множество тех точек xÎW, при которых  U(х)£t, принадлежит семейству U.

Поскольку s-алгебра U замкнута относительно операции взятия до­полнений, то в определении измеримости можно неравенство £ заме­нить на любое из неравенств ³, >, <. Из самого определения следует, что  n-измеримые функции  образуют замкнутый класс наподс бие класса бэровских функций.

Как уже было указано,s-алгебра может быть выбрана весьма произ­вольно, и , в частности, следующим образом: сначала на пространстве WÎRⁿ определяются n-мерные интервалы, затем с помощью операций алгебры множеств из этих интервалов могут быть построены множества более сложной структуры и сформированы семейства множеств. Среди все возможных семейств, можно отобрать такое, которое содержит все открытые подмножества в W. Подобное построение приводит к следующему определению.

Определение 1.6. Наименьшая s-алгебра  U^b , содержащая все откры­тые (а следовательно, и все замкнутые) подмножества множествами WÌ Rⁿ называется борелевской s-алгеброй, а его множества - борелевскими.

Оказывается, что класс беровских функций B тождествен классу функ­ций, измеримых относительно s-алгебры U^b борелевских множеств.

Теперь мы можем четко определить понятие случайной величины и вероятностной функции ее распределения.

Определение 1.7. Случайной величиной Х называется действительная функция Х =U(х), хÎW, измеримая относительно s-алгебры U, входящей в определение вероятностного пространства.

Определение 1.8. Функцией распределения случайной величины Х называется функция F(t) = Р{X £ t}, определяющая вероятность того, что случайная величина Х не превосходит значения t.

По заданной функции распределения F однозначным образом может быть построена вероятностная мера, и наоборот.

Рассмотрим основные вероятностные закономерности на примере ко­нечного множества W. Пусть A,BÌ W. Если А и В содержат общие эле­менты, т.е. АВ¹0, то можно записать: А+В=А+(В-АВ) и  В = АВ+(В-АВ), где в правых частях стоят непересекающиеся множества (т.е. несовме­стимые события), а следовательно, по свойству аддитивности вероятно­стной меры: Р(А+В) = Р(В-АВ)+Р(А),  Р(В) = Р(АВ)+Р(В-АВ); отсюда сле­дует Формула для суммы вероятностей произвольных собы­тий: Р(А+В) = Р(А) + Р(В) - Р(АВ).

Если при вычислении вероятности события А никаких условий не на­лагается, то вероятность Р(А) называется безусловной. Если событие А реализуется, например, при условии, что реализовалось событие В, то говорят об условной вероятности, обозначая ее символом Р(А/В). В аксиоматической теории вероятностей по определению полагается:

Р(А/В) = Р(АВ)/Р(В).

Чтобы интуитивно это определение стало понятным, рассмотрим, нап­ример, следующую ситуацию. Пусть в коробке лежат k бумажек, помеченных буквой А ,r бумажек, помеченных буквой В , m  бумажек, поме­ченных буквами А·В  и n пустых бумажек. Всего имеется р = k + r + n + m   бумажек. И пусть из коробки по очереди вытаскиваются одна бумажка за другой, причем после каждого вытаскивания отмечается тип вытащенной бумажки и она снова кладется в коробку.  Результаты очень большого числа подобных испытаний записываются. Условная веро­ятность  Р(А/В) означает, что событие А рассмат­ривается только в связи с реализацией события В. В данном примере это означает, что необходимо подсчитать число  вытащенных бумажек с буквами А·В и буквой В и первое число разделить на сумму  первого и второго чисел. При достаточно большом числе испытаний это отношение будет стремиться к числу ,  определяющему условную вероят­ность Р(А/В). Аналогичный подсчет других бумажек покажет, что

  и P(B)=

Вычисляя отношение

убеждаемся, что оно как раз совпадает с ранее вычисленным нами зна­чением для вероятности Р(А/В). Таким образом, получаем

Р(А·В) = Р(A/В)·Р(В).

Проводя аналогичные рассуждения, поменяв местами А и В, получим

Р(А·В) = Р(В/А)·Р(А)

Равенства

Р(А·B) = Р(А/В)·Р(В) = Р(В/А)·Р(А)

называют теоремой умножения вероятностей.

Рассмотренный пример позволяет также наглядно убедиться в спра­ведливости следующего равенства при A·B¹Æ  :

Р(A + В) == Р(А) + Р(В) - Р(А·В).                     

Пример 1.1. Пусть дважды бросается рсается игральная кость и требуется определить вероятность P(A/B) выпадения в сумме 10 очков, если в первом бросании выпало 4.

Выпадение во втором бросании 6 имеет вероятность  1/6.  Следовательно,

Пример1.2.  Пусть имеется 6 урн :

в урне типа А₁ - два белых и один черный шар, в урне типа А₂- два белых и два черных шара, в урне типа А₃ - два черных и один белый шар. Имеется 1 урна типа А₁, 2 урны типа А₂ и 3 урны типа А₃. Случайно выбирается урна и из нее шар. Какова ве­роятность, что этот шар белый?  Обозначим через В событие вытаски­вания белого шара.

Чтобы решить задачу, предположим, что некоторое событие В реали­зуется только вместе с одним из n несовместимых событий А₁,..., А_n, т.е. В = , где события ВА_i и ВА_j с разными индексами i и j несовместимы. Из свойства аддитивности вероятности Р следует:   

Подставляя сюда зависимость (1.1), получаем

эта формула носит название формулы полной вероятности. Для решения последнего примера воспользуемся формулой полной вероятности. Так как белый шар (событие В) может быть взят из одной из трех урн (события А₁, А₂, А₃ ), то можно записать

     В = А₁В + А₂В  + А₃В  .

Формула полной вероятности дает

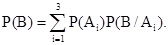
Подсчитаем вероятности, входящие в эту формулу. Вероятность, что шар взят из урны типа А₁ , очевидно равна Р(А₁) = 1/6, из урны типа А₂: Р(А₂) = 2/6 == 1/3  и из урны типа А₃: P(A₃) = 3/6 = 1/2. Если шар взят из урны типа А₁, то Р(В/А₁) = 2/3 , если из урны типа А₂, то  Р(В/А₂)=1/2, а если из урны типа А₃, то Р(В/А₃)= 1/3. Таким образом,

Р(В) =(1/6)(2/З)+ (1/3) (1/2) + (1/2) (1/3) =  4/9.

Условная вероятность Р(В/А) обладает всеми свойствами вероятности Р(В/А)³0, В(В/В) = 1  и  P(В/А) аддитивна.

Поскольку

Р(А·В) == Р(В/А)-Р(А) = Р(А/В)·Р(В) ,

то отсюда следует, что  если А не зависит от В, то есть если

Р(А/В) = Р(А),

то и В не зависит от А, т.е.  Р(В/А) = Р(В).

Таким образом, в случае независимых событий теорема умножения принимает  наиболее простой вид:

Р(А·В) = Р(А)·Р(В)                                 (1.3)

Если события А и В независимыми, то независимы также и  каждое из следующих пар событий: (A,В), (А,B), (A,В).  Убедимся, например, что если А и В независимы, то независимы и А и Б . Поскольку Р(В/А) + Р(B/А) = I, то отсюда с учетом условия независимости собы­тий А и В, т.е. условия  Р(В/А) = Р(В), следует: Р(В/А) = 1 - Р(В) = Р(В).

События могут быть попарно независимыми, но оказаться зависим-ыми в совокупности. В связи с этим вводится также понятие взаимной неза­висимости: события  А₁,..., А_n называются взаимно независимыми, если для всякого подмножества  Е индексов 1,2,...,n выполняется равен­ство 

   

На практике нередко  приходится оценивать  вероятности гипотез после того, как проведено некоторое испытание. Пусть, например, со­бытие В может реализоваться лишь с одним из несовместимых событий А₁,...,А_n , т.е.  и пусть событие В реализовалось.Требуется найти вероятность гипотезы (события) А_i при условии,

что В произошло. Из теоремы умножения

Р(А_iВ) = Р(В) Р(А_i/В) = Р(А_i) Р(В/А_i)

В лекции "2.20 Русская усадьба XVIII века" также много полезной информации.

cледует

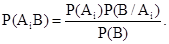
С учетом формулы полной вероятности для Р(В) отсюда следует

 

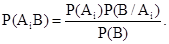
Эти формулы носят название формул Байеса.

Пример 1.3. Пусть в примере 1.2 вытащен белый шар и требуется оп­ределить,  какова вероятность, что он взят из урны типа 3.