Теория дифференциальных уравнений в частных производных 1-го порядка

Теория дифференциальных уравнений в частных производных 1-го порядка

Геометрическая теория  уравнений 1-го порядка в случае двух независимых переменных

В данном разделе мы будем рассматривать дифференциальные уравнения вида:                           (1)

(квазилинейное уравнение), где коэффициенты a(x,y,v), b(x,y,v), с(x,y,v) – непрерывные функции своих аргументов, имеющие и непрерывные частные производные.

Геометрически решение этого уравнения v=v(x,y) будем изображать в виде некоторой поверхности. Рассмотрим на интегральной поверхности точку Р и продифференцируем функцию v по любому касательному направлению в этой точке. Запишем дифференциал dv=v’_xdx+v’_ydy. Это выражение удобно переписать в виде v’_xdx+v’_ydy+(-1)dv=0.

Введем обозначение Монжа (франц. математик) , .

Тогда предыдущее выражение перепишется в виде pdx+qdy+(-1)dv=0. Перепишем как скалярное произведение (p,q,-1)(dx,dy,dv)=0.

Так как dx,dy,dv – проекции бесконечно малого касательного вектора в точке Р, и этот вектор  - произвольный касательный вектор в этой точке, то из равенства нулю скалярного произведения следует, что вектор (p,q,-1) – нормаль к поверхности в точке Р.

Запишем уравнение (1) в обозначениях Монжа: ap+bq+c(-1)=0. Или, рассматривая как скалярное произведение найдем: (a,b,c)(p,q,-1)=0. Откуда видно, что если v(x,y) – решение нашего уравнения, то нормаль к интегральной поверхности в каждой точке пространства x,y,v должна быть ортогональна вектору (a,b,c) заданному в этой точке. Таким образом, д. у. (1) накладывает на интегральную поверхность единственное требование: в каждой точке нормаль к интегральной поверхности должна быть ортогональна заданному в этой точке вектору (a,b,c).

Рекомендуемые материалы

Если в точке Р провести касательную плоскость к интегральной поверхности, то нормаль к интегральной поверхности будет также и нормалью к касательной плоскости.

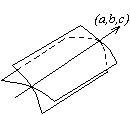
Очевидно, что трехмерному вектору (a,b,c) можно провести бесконечное однопараметрическое множество нормалей и соответствующее бесконечное множество допустимых касательных плоскостей к интегральной поверхности. Введенное нами множество касательных плоскостей называется пучком Монжа, а вектор (a,b,c), который они все пересекают, называется осью Монжа.

Аналогия

,  - tg угла наклона в каждой точке.

Ищем поверхность, которую в каждой точке касается вектор (a,b,c).

Рассмотрим в некоторой точке пространства (x,y,v) бесконечно малый вектор (dx,dy,dv), коллинеарный в этой точке вектору (a,b,c). У коллинеарных векторов проекции пропорциональны и можем записать:

Эти три равные величины обозначим dS. Разделив эти три равенства на dS, получим 3 дифференциальных уравнения:

 , ,                                               (2)

Мы получили три д.у., которые называются уравнениями характеристик для д. у. (1). Всякое решение этой системы дифференциальных уравнений:

                                                                             (3)

замечательно тем, что по построению, в каждой точке кривые (3) касаются вектора (a,b,c) (зависят еще от начальных условий).

Теорема

Всякая поверхность v=v(x,y), которую можно покрыть однопараметрическим множеством характеристик (построить из однопараметрического множества характеристик) является интегральной поверхностью уравнения (1).

Обратно: всякую интегральную поверхность можно покрыть однопараметрическим множеством характеристик.

Докажем первую часть теоремы:

Проведем в пространстве некоторую кривую, которую зададим параметрически. И потребуем, чтобы эта кривая ни в одной точке не касалась вектора (a,b,c). Из каждой точки этой кривой проведем с помощью д. у. (2) характеристики:

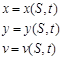
Если, построенное таким образом однопараметрическое множество характеристик образует поверхность, то эта поверхность будет интегральной. Действительно, рассмотрим произвольную точку Р на этой поверхности. Через эту точку проходит некоторая характеристическая кривая (по построению), которая в точке Р касается соответствующего вектора (a,b,c). В этом случае нормаль к построенной поверхности в данной точке будет одновременно и нормалью к характеристике, и, следовательно, нормалью к вектору (a,b,c), откуда следует, что построенная поверхность удовлетворяет в данной точке единственному требованию, которое накладывает д. у. (1) на интегральную поверхность. И так для каждой точки построенной поверхности, откуда следует, что поверхность является интегральной.

Докажем вторую часть теоремы:

Нам задана интегральная поверхность v=v(x,y). Мы докажем данную теорему, если покажем, как ее можно покрыть однопараметрическим множеством характеристик. На плоскости x,y построим с помощью дифференциальных уравнений:

,                                 (4)

в правые части которых подставлена функция v=v[x(S),y(S)], однопараметрическое множество кривых, проходящих через кривую С.

Через каждую такую кривую проведем цилиндрическую поверхность (образующие которой параллельны оси v) до пересечения с интегральной поверхностью. Вдоль кривой на интегральной поверхности выполняются дифференциальные уравнения (4). Кроме того, дифференцируя функцию v (она задана) вдоль полученной кривой, найдем:

, подставим из (4): .

И так как поверхность является интегральной, то в силу д. у. (1) вдоль построенной кривой выполняются уравнения (4) и уравнение  (5).

Нетрудно видеть, что они совпадают с уравнениями (2) и, таким образом построенная кривая является характеристикой. Ясно, что таким образом можно покрыть всю поверхность однопараметрическим множеством характеристических кривых.

Задача Коши для дифференциального уравнения  (1)

Пусть на плоскости x,y параметрически задана кривая x=x(t), y=y(t). t – параметр вдоль кривой, и пусть в каждой точке этой кривой задана функция v=v(t). Полученная таким образом кривая С представляет собой пространственную кривую заданную параметрически.

Для дальнейшего потребуем, чтобы функции x(t), y(t), v(t) были непрерывными вместе со своими первыми производными.

Задача Коши: заключается в нахождении решения уравнения (1), которое принимает заданное значение v(t) на кривой C. Другими словами требуется найти в окрестности C’ интегральную поверхность, проходящую через кривую С.

Для построения решения воспользуемся характеристиками

, ,                                                (2)

Решая уравнение (2) из каждой точки кривой С выпустим характеристику. Пусть уравнения этих характеристик имеют вид:

,

(t входит через начальные данные). Эти уравнения можно решить относительно параметров S и t: , .

Подставим найденные решения в функцию v:  .

Однако, разрешить уравнение относительно S и t не всегда возможно.

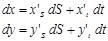
Заменим дифференциалы малыми конечными приращениями. Обозначим индексом «0» значения величин на начальной кривой C:

 или .

Условие разрешимости полученной системы относительно S  и t – это неравенство нулю определителя из коэффициентов при S и t:

, или .

Так как x’_S=a, и y’_S=b, то   (3).

Таким образом, если выполняется  условие (3) на начальной кривой (а в силу непрерывности входящих в якобиан величин он будет неравен нулю в некоторой окрестности начальной кривой), то мы можем в окрестности начальной кривой найти поверхность v=v(x,t) проходящую через эту кривую. Продифференцируем эту поверхность вдоль любой характеристики:

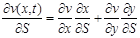
Используя уравнения характеристик, получаем  .

Таким образом, видим, что построенная поверхность удовлетворяет д. у. (1), и, следовательно, является его решением.

Рассмотрим теперь случай, когда якобиан (3) равен нулю: , а решение v=v(x,y) при этом существует. Покажем, что в этом случае начальная кривая сама является характеристикой.

Перепишем якобиан в виде: . Сократим на dt и поделим на ab , откуда получим два уравнения ,   (*).

Так как решение задачи по предположению существует, то функция v(x,y) выполняется и на начальной кривой, и, следовательно, можем дифференцировать эту функцию вдоль начальной кривой:

Или, воспользовавшись уравнением характеристик:

, v есть решение уравнения (1).  (**).

Равенства (*) и (**) говорят о том, что начальная кривая будет характеристикой.

Далее покажем, что в случае, когда якобиан равен нулю, решений существует бесконечно много. Пусть задана начальная кривая C, которая является характеристикой. На ней Δ=0 и решение существует. Требуется найти интегральную поверхность, проходящую через кривую C. Проведем любую кривую С₁, которая пересекает нашу кривую в некоторой точке, и на которой якобиан нигде не равен нулю. Как было показано выше, задача Коши для С₁ разрешима и мы методом характеристик можем построить интегральную поверхность. Так как коэффициенты a,b,c являются непрерывными функциями, то задача Коши для о. д. у. (2) имеет единственное решение. Откуда следует, что через точку пересечения кривых может проходить единственная характеристика, которая, очевидно, совпадает с кривой С. Таким образом, мы построили решение (если C не совпадет, то решение будет не единственно, что не так по условию).

Проведем через точку пересечения кривых С и С₁ кривую С₂, на которой тоже Δ≠0. Также как и в предыдущем случае можно построить интегральную поверхность, проходящую через кривую С. Ясно, что таким образом можно построить бесконечное множество поверхностей. Полученные результаты сформулированы в виде теоремы:

Теорема

Если якобиан (3) на начальной кривой не равен нулю, то задача Коши для уравнения (1) разрешима единственным образом. В том случае, когда якобиан равен нулю на начальной кривой и решение существует, то это решение не единственно.

Общие требования к постановке классических задач для уравнений в частных производных

Эти требования впервые сформулировал Адамар. Задача для уравнения в частных производных называется корректно поставленной (по Адамару), если она удовлетворяет следующим требованиям:

1. Решение задачи должно существовать

На решение задачи не должно быть наложено слишком много дополнительных условий, и они не должны противоречить друг другу.

2. Решение задачи должно быть единственным

Точки ветвления – параметры, при которых возникает неединственность решения (например существует 2 решения в одной точке).

3. Решение задачи должно быть устойчивым

А именно, малому изменению данных задачи должно отвечать малое изменение решения. В противном случае задача называется неустойчивой. Адамар считал, что поскольку данные задачи получаются из экспериментов, которые всегда содержат ошибки, то для неустойчивой задачи ошибки эксперимента будут приводить к каким угодно решениям, а такие задачи решать не имеет смысла.

Пример:

При любом возмущении поверхности на границе раздела двух сред ртути и воды, кусок ртути начнет падать.

Рассмотрим пример , здесь a=1, b=1, c=0. Поэтому уравнения характеристик можно записать:

, , .

Параметр S можно исключить: 1-ое и 3-е разделим на 2-ое:

,

Из 1-го уравнения следует, что характеристиками уравнения (1) будут прямые (угол наклона 45º) .

Константу С определим при t=0 в точке пересечения характеристики с осью абсцисс. При t=0 x=x₀ (где x₀ – значение абсциссы в точке, где характеристика пересекает ось абсцисс), тогда .

Из равенства  следует, что вдоль этой характеристики u=const. Вдоль каждой характеристики константа может быть своя, поэтому в общем случае, функция u не является постоянной, она постоянна только вдоль характеристики.

Для дальнейшего удобно записать общее решение уравнения (1). Введем новые переменные ξ=x-t, η=x+t, и сделаем замену, тогда:

,

При подстановке производных в уравнение, получим , откуда , следовательно, u зависит только от ξ, и общее решение .

Пример 1

Требуется найти решение в полосе, ограниченной отрезком оси абсцисс (x’;x’)’ и характеристиками, выходящими из точек x’ и x’’. Потребуем также, чтобы функция u принимала заданные значения φ(x) на отрезке x’x’’.

Полагая в общем решении t=0, найдем, что u(0,x)=f(x)=φ(x), откуда следует, что решение нашей задачи u(x,t)=φ(x-t) для конкретной характеристики x-t=x₀, проходящей через точку x₀ принимает значение u=φ(x₀). Это константа на выбранной характеристике.

Таким образом, решение поставленной задачи существует.

Пример 2

Пусть требуется найти решение уравнения (1) в полосе, ограниченной отрезком (0;t’) оси ординат и характеристиками, выходящими из точек t=0 и t=t’. И пусть функция u задана на указанном отрезке оси ординат u=ψ(t) (ψ – известная функция).

Для решения задачи воспользуемся снова общим решением. Константу С на характеристике определим при x=0: x=C+t, следовательно C=-t₀. t₀ – точка, в которой характеристика пересекает ось ординат. Тогда уравнение характеристик x=t-t₀ или x-t=-t₀. Общее решение запишем в виде произвольной функции u=f[-(x-t)].

Подставляя уравнение характеристик u=f(t₀) видим, что на характеристике u принимает постоянное значение f(t₀).

Если мы возьмем функцию f(ξ)≡ψ(S), то наше решение будет иметь вид u=ψ[-(x-t)]. u на характеристике будет принимать значения u=ψ(t₀).

Таким образом, решение данной задачи также существует, мы его нашли.

Пример 3

Рассмотрим теперь задачу поиска решения в полосе, показанной на рисунке с дополнительными данными, заданными на отрезках (0;x’) и (0;t’).

Разбивая эту полосу на 2 полосы характеристикой, выходящей из начала координат x=t, сведем нашу задачу к двум предыдущим, и, таким образом, найдем решение, для непрерывности которого необходимо только потребовать, чтобы φ(0)=ψ(0), т. е. функции φ и ψ в начале координат совпадают.

Пример 4

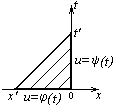
Рассмотрим задачу для области, показанной на рисунке. При этом потребуем, чтобы на отрезке (x’;0) решение принимало значение u=φ(x), а на отрезке (0;t’) u=ψ(t). Эта задача похожа на предыдущую, но решение ее не существует. Если потребовать, чтобы решение задачи при t=0 принимало значение φ(x), то можем записать u=φ(x-t), где φ – известная (заданная) функция.

При x=0 эта функция принимает значение φ(-t)≠ψ(t). Таким образом, в общем случае удовлетворить второму условию невозможно, следовательно, поставленная задача не существует.

Пример 5 (пример неединственного решения)

Пусть требуется найти решение уравнения (1) в области, показанной на рисунке, ограниченной отрезком (a;b) оси абсцисс и характеристиками, выходящими из этих точек. И пусть дополнительные данные задачи заданы на отрезке (a’;b’):  u=φ(x) при a’≤x≤b’. Для того, чтобы решить поставленную задачу продолжим непрерывным образом функцию φ(x) на весь отрезок (a;b), и продолженную функцию обозначим , a≤x≤b. Как мы знаем, решение такой задачи существует и единственно. Однако, осуществляя продолжение различным образом, мы получим различные решения задачи. Откуда следует, что исходная поставленная задача имеет неединственное решение.

Пример 6 (пример неустойчивого решения, рассмотрел Адамар)

Рассмотрим в полуплоскости y>0 решение задачи Коши для уравнения Лапласа: .

Пусть первое решение удовлетворяет при y=0 начальным условиям: u₁(x,0)=0,   (2 условия - 2 произвольные функции).

Очевидно, решением этой задачи является тождественный ноль u₁(x,y)≡0.

Вторую задачу поставим так, чтобы она удовлетворяла при y=0 условиям:  (производная по нормали)

Ещё посмотрите лекцию "3 - Поиски и разведка месторождений" по этой теме.

Простой проверкой можно установить (методом разделения переменных), что решением данной задачи будет  .

При достаточно больших n начальные условия в данной задаче отличаются сколь угодно мало. В то же время  растет как показательная функция . Из анализа мы знаем, что показательная функция растет быстрее любой степени аргумента, поэтому при больших n разность  будет сколь угодно велика за счет . Следовательно, сколь угодно малому изменению данных задачи может отвечать неограниченное изменение решения.

На самом деле многие физические задачи являются неустойчивыми с точки зрения физики. Для их решения применяют регуляризирующие численные методы.

Пример:

Концы стержня находятся в воде T=const. Через промежуток времени определить то, что было раньше невозможно.