Вывод классических уравнений математической физики

Вывод классических уравнений математической физики

Уравнение  нельзя решить, так как при неограниченно малом изменении начальных условий, решение изменится значительно. Хотя по теореме Коши-Ковалевской решение существует и единственно. Решение уравнения  уже возможно.

Уравнение Лапласа

Будем выводить его неправильно, так, как выводил его сам Лаплас:

Ньютон вывел закон всемирного тяготения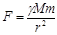

( на единицу массы). «Между любыми двумя телами действует сила притяжения, прямопропорциональная их массам и обратнопропорциональная квадрату расстояния между ними». Лапласу не понравилась сила, действующая через вакуум на большой траектории, и он предположил, что вокруг всякого тела массой М возникает некоторая субстанция, интенсивность которой , где r – расстояние между точкой с координатами (x₀,y₀,z₀) где расположена масса M, и точкой наблюдения с координатами (x,y,z). . Далее Лаплас нашел, что с помощью этой субстанции можно вычислить проекции силы , если вычислять ее по формуле

, ,

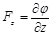
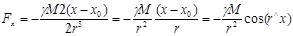
точно также запишем

Рекомендуемые материалы

,  

.

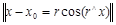
В дальнейшем Лаплас предложил пользоваться не самим выражением для потенциала, а тем дифференциальным уравнением, которому оно удовлетворяет. Получим это д. у.:

Вычислим сначала вторую производную от потенциала по x:

, аналогично

, .

Складывая эти три частные производные, получаем уравнение Лапласа

                                     (1)

Исторически это было первое уравнение с частными производными полученное математиками. Хотя уравнение Лапласа было получено для потенциала тяготения, оно описывает распределение большого количества совершенно различных физических величин, в частности уравнению (1) подчиняется потенциал электростатического поля, безвихревого течения идеальной жидкости, стационарное распределение концентрации в диффузионном поле или распределение температур.

В двухмерном случае уравнение Лапласа принимает вид

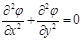
тогда говорят о плоской постановке задачи.

Уравнение теплопроводности

Рассмотрим некоторый объем V заполненный веществом и ограниченный поверхностью S. Обозначим через ρ плотность вещества в данном объеме, через С – его теплоемкость. И пусть в объеме за счет некоторых источников выделяется тепло, при этом через q обозначим количество тепла, которое выделяется в единице объема в единицу времени. Общее количество тепла, которое выделится в единицу времени в данном объеме, будет равняться  , это количество тепла Q пойдет на нагрев тела.

Обозначим Q₁ – количество тепла, которое идет на нагрев тела в единицу времени и на теплоотдачу к внешней среде через границу тела. Q₂ – количество тепла, которое уходит (а может наоборот приходит) через границу тела в единицу времени. Тогда можно записать закон сохранения тепла Q=Q₁+Q₂. Количество тепла, которое содержится в единице объема равно ρСT (C – теплоемкость единицы массы). Тогда в объеме dV будет содержаться количество тепла равное ρСTdV. Изменение этого количества тепла за время dt будет равно [ρСT(t+dt)- ρСT(t)]dV. Поделив на dt, получим изменение количества тепла в объеме dV в единицу времени: .

Переходя к пределу при dt→0, и учитывая, что температура зависит не только от времени, но и от координат, получим . Интегрируя по всему объему, найдем количество тепла, которое тратится на нагрев тела в единицу времени .

Согласно закону Фурье для теплоотдачи (открытому на самом деле Ньютоном) через единицу поверхности с нормалью   в единицу времени проходит количество тепла равное , где производная берется в направлении нормали к телу. Тогда через единицу поверхности dS в единицу времени теряется количество тепла равное . Интегрируя по всей поверхности тела, найдем количество тепла, которое теряет тело за счет теплопроводности

.

Выражая проекцию  через градиент , величину Q₂ будем записывать в виде .

Используя закон сохранения тепла и подставляя в него величины Q₁ и Q₂, получим закон сохранения тепла в интегральной форме:

.

Для получения д. у. преобразуем второй интеграл по формуле Остроградского-Гаусса к интегралу по объему :

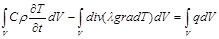
Собирая все интегралы в левой части запишем

, откуда получаем

Уравнение теплопроводности

                                            (2)

Так как  (есть вектор с компонентами), то в декартовой системе координат:

.

Если λ является константой, то ее можно вынести из под знака производной, а, поделив результат на Cρ, придем к выражению:

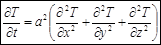
 - коэффициент температуропроводности (квадрат пишут, чтобы подчеркнуть, что это положительная величина).

λ – коэффициент теплопроводности.

Уравнение теплопроводности также описывает многочисленные физические процессы. Ему подчиняется диффузия концентрации, распределение вероятности нахождения частицы в классической квантовой механике, размножение колоний микробов и т. д.

Вывод уравнения колебаний струны

Струной называется тонкая нить, которая сопротивляется натяжению, но не сопротивляется изгибу.

Рассмотрим элемент струны длиной dx. u – отклонение струны от положения равновесия. Длина малого элемента струны (по т. Пифагора) с точностью до малых 2-го порядка .

В дальнейшем будем рассматривать малые колебания струны, предполагая, что u<<1, u_x<<1. Тогда под корнем можно пренебречь квадратом малой величины, и с точностью до малых высокого порядка писать ds=dx.

Последнее выражение означает, что при малых колебаниях длина струны практически не меняется.

В силу закона Гука усилие натяжения струны пропорционально удлинению, так как при малых колебаниях длина струны не меняется, то натяжение можно считать постоянным. Обозначим силу натяжения F, на бесконечно малый элемент она действует в направлении показанном на рисунке. Обозначим через α угол между направлением касательной к струне и осью x.

Проекция силы натяжения на ось u в точке x+dx будет:

.

Пренебрегая под корнем производной найдем

.

Вычисляя проекцию в точке x точно также найдем, что («-» так как сила действует в противоположном направлении). Суммарная проекция сил натяжения, действующих на элемент струны равна   разлагая в ряд в окрестности точки x найдем .

Вычислим теперь силу инерции, действующую на данный элемент струны. Обозначим через ρ(x) погонную плотность среды (массу единицы длинны), тогда масса элемента dx будет ρ(x)dx.

Так как u – отклонение струны, то u’_t будет представлять собой скорость перемещения элемента струны, а u’’_tt будет ускорение струны.

Произведение массы на ускорение согласно закону Ньютона мы должны приравнять к силам .

Поделив на ρ  и введя обозначение , найдем:

Уравнение колебаний струны

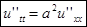
 является скоростью распространения колебаний по струне.

Наряду с одномерным уравнением колебаний в мат. физике рассматривают также двумерное уравнение колебаний:

(мембраны, акустика).

И трехмерное уравнение колебаний:

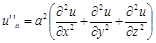
Эти уравнения, как и предыдущие, описывают множество различных физических процессов.

Вывод уравнения переноса

Вывод этого уравнения рассмотрим на примере вывода уравнения, которое описывает бесстолкновительное движение множества молекул в отсутствие внешних полей.

Рассмотрим некоторое множество молекул, находящихся в малом объеме dxdydz. Среди этих молекул выберем подмножество таких, которые имеют близкие скорости, расположенные в диапазонах: [u_x,u_x+du_x], [u_y,u_y+du_y], [u_z,u_z+du_z]. Введем функцию распределения молекул по скоростям f(x,y,z,u_x,u_y,u_z,t) такую, чтобы произведение f(x,y,z,u_x,u_y,u_z,t)dxdydzdu_xdu_ydu_z (*) давало нам число молекул находящихся в объеме dxdydz и имеющих близкие скорости из указанного выше диапазона, например:

В равновесном случае число частиц в единице объема .

Шестимерное пространство x,y,z,u_x,u_y,u_z  называется фазовым пространством.

Объем dxdydzdu_xdu_ydu_z называется бесконечно малым объемом в фазовом пространстве.

Выделим в фазовом пространстве некоторую группу частиц, находящихся в малом объеме и обладающих близкими скоростями и будем следить за частицами этой группы. Так как столкновений нет, что число частиц в этой группе будет сохраняться (если бы столкновения были, то молекулы могли бы получить неблизкие скорости). В момент t число молекул можно посчитать по формуле (*). В момент t+dt координаты частиц изменятся, но так как отсутствуют столкновения и внешние поля, то скорости частиц останутся неизменными. Может измениться также и фазовый объем, который они занимают в момент t, поэтому в момент t+dt число этих частиц будет выражаться формулой:

        (1)

новый объем .

Так как число частиц сохраняется, мы можем записать:

                 (**)

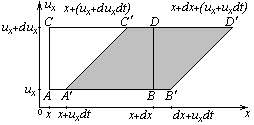
Покажем, что фазовый объем в нашем случае не изменяется. Для этого рассмотрим сначала, как изменяется проекция фазового объема. В момент t+dt точки A,B,C,D передвинутся. Нетрудно видеть, что получится параллелограмм, верхнее и нижнее основания которого равны dx, а высота du_x. Площадь этого параллелограмма будет по-прежнему du_xdx, то есть . Точно также можно показать и для других проекций , . Так как элементарный фазовый объем есть произведение этих величин, то он не изменится. Фазовые объемы слева и справа в (**) можно сократить:

"4.15 Творчество К.С. Петрова-Водкина" - тут тоже много полезного для Вас.

.

Функцию в левой части равенства разложим в ряд по малым приращениям ее аргументов и, ограничиваясь малыми 1-го порядка, получим:

.

В оставшемся дифференциальном операторе можно вынести dt и на него сократить. В результате получим уравнение переноса

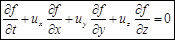
Это уравнение впервые получил Больцман (правда с учетом столкновения), применяется для описания кинетики.