Вычет аналитической функции в изолированной особой точке

   §18. Вычет аналитической функции в изолированной особой точке.

   Пусть точка  z₀  является изолированной особой точкой однозначной аналитической функции

 f(z) . Согласно предыдущему,  в окрестности этой точки  f(z)  может быть представлена единственным образом рядом Лорана :  где      

Определение. Вычетом   аналитической функции  f(z)  в  изолированной особой точке  z₀ 

 называется комплексное число, равное значению интеграла  , взятому в положительном направлении по любому замкнутому контуру, лежащему в области аналитичности функции и содержащему внутри себя единственную особую точку  z₀.

   Вычет обозначается  символом  Res [f(z), z₀].

   Нетрудно видеть, что вычет в правильной или устранимой особой точке равен нулю.

   В полюсе или существенно особой точке вычет равен коэффициенту  с_-1 ряда Лорана:

                                          .

Рекомендуемые материалы

Пример.  Найти вычет функции .

  {Пусть  Легко видеть, что

коэффициент  с_-1 получится при умножении слагаемых при  n = 0: Res[f(z),i] = } 

  Часто  удается вычислять вычеты функций более простым способом. Пусть функция  f(z)  имеет в т.  z₀  полюс первого порядка. В этом случае разложение функции в ряд Лорана имеет вид (§16): . Умножим это равенство на  (z − z₀)  и  перейдем к пределу при . В результате получим:  Res[f(z), z₀] =   Так, в

"8.3. Постмодернистская модель мира" - тут тоже много полезного для Вас.

последнем примере имеем Res[f(z),i] =.

   Для вычисления вычетов в полюсах более высокого порядка  следует умножить функцию

на   (m − порядок полюса) и продифференцировать полученный ряд  (m −1)  раз.

В этом случае имеем:  Res[f(z), z₀]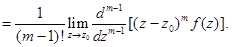

Пример. Найти вычет функции    в т. z = −1.

{ Res[f(z), −1]  }