Знакоопределенные квадратичные формы. Критерий Сильвестра
Знакоопределенные квадратичные формы. Критерий Сильвестра.
Определение 1.30 Квадратичная форма 
называется положительно (отрицательно) определенной, если для любого ненулевого вектора 
(соответственно 
).
Положительно или отрицательно определенная квадратичная форма называется знакоопределенной. Если в определении 1.30 строгие неравенства заменить нестрогими, то получим определения положительно (отрицательно) полуопределенной квадратичной формы.
Квадратичная форма, не являющаяся ни знакоопределенной, ни полуопределенной (положительно или отрицательно), называется квадратичной формой общего вида.
Свойства квадратичной формы легко распознать, приведя ее к каноническому виду.
Обозначим: 
- сигнатуру, ранг некоторой квадратичной формы и размерность пространства соответственно.
Утверждение 1.22 Квадратичная форма :
1) положительно определена 
;
2) отрицательно определена 
;
Рекомендуемые материалы
3) положительно полуопределена 
;
4) отрицательно полуопределена 
.
Доказательство. (1): если форма положительно определена, то, записав ее в нормальном виде
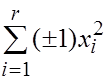
и предполагая, что 
, получим, что на векторе 
форма принимает нулевое значение, что невозможно. Итак, 
. Опять-таки, предполагая отрицательность хотя бы одного коэффициента в записанной выше сумме, легко найдем такой ненулевой вектор, на котором данная форма принимает отрицательное значение. Следовательно, если форма положительно определена, то ее нормальный вид есть 
.
Обратное очевидно.
Утверждение (2) доказывается точно так же.
Утверждения (3) и (4) должен доказать читатель самостоятельно.
Но чтобы судить о знакоопределенности (и даже о полуопределенности) квадратичной формы, совсем не обязательно приводить ее к каноническому виду. Ниже доказывается важное утверждение, называемое критерием Сильвестра, на основании которого можно распознать знакоопределенность любой квадратичной формы, имея в распоряжении ее матрицу в любом базисе (даже не обязательно ортонормированном).
Теорема 1.18 (Критерий Сильвестра) Пусть квадратичная форма
задана в каком-то базисе в виде
(1)
(матрица 
, вообще говоря, не совпадает с матрицей линейного оператора 
!).
Тогда для положительной определенности данной формы необходимо и достаточно, чтобы все определители
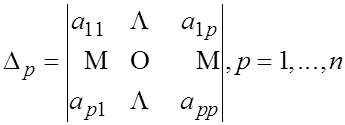
были положительны.
Доказательство. Исходное представление (1) преобразуем таким образом, чтобы выделить все члены, содержащие 
:
(1а)
(в предположении 
).
Приравнивая коэффициенты при произведении 
, получим:
,
откуда
(2)
Выражение (2) очень похоже на выражение для пересчета матрицы на первом шаге процедуры Гаусса решения системы линейных уравнений (первый семестр!). Этот шаг, напомним, состоит в вычитании из каждой 
-ой строки матрицы (начиная со второй) первой строки, умноженной на 
( в предположении, разумеется, что ведущий элемент 
отличен от нуля). Кроме того, индекс столбца 
в методе Гаусса изменялся от единицы.
Но матрица квадратичной формы предполагается симметрической в любом базисе (по определению), и потому 
. Требование же 
ничего не меняет, так как из формулы (2) при подстановке в нее 
получается 
, что предполагается при переходе от формулы (1) к формуле (1а).
Итак, мы можем отождествить введенное преобразование с первым шагом метода Гаусса. После него матрица квадратичной формы примет вид:
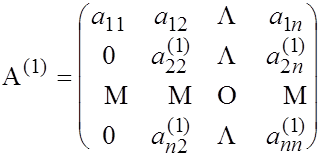
После этого подвергнем подматрицу 
точно такому же преобразованию (полагая, как и в методе Гаусса, что новый ведущий элемент 
отличен от нуля).
После 
шага таких элементарных преобразований, где 
-ранг квадратичной формы (и ранг матрицы 
), получим матрицу
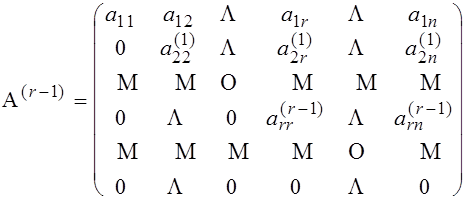
Данное преобразование матрицы определяет преобразование базиса, согласно которому новые координаты векторов (новые переменные квадратичной формы) связаны со старыми формулами:
(3)
Квадратичная форма при этом принимает вид:
(4)
Поскольку элементарное преобразование, выполняемое на каждом шаге метода Гаусса, не меняет ни ранга, ни определителя матрицы (первый семестр!), мы можем написать:
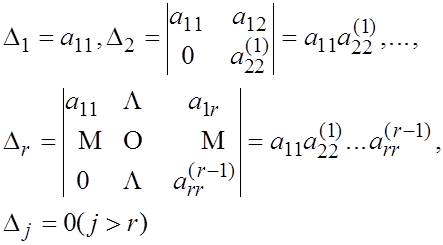
Полагая для удобства 
, получим простую формулу:
,
откуда
,
и формула (4) примет вид:
(5)
Мы привели исходную форму к каноническому виду (описанный метод называется методом Лагранжа). Тогда, используя утверждение 1.22, можно сделать вывод, что наша форма положительно определена тогда и только тогда, когда в (5) и 
, т.е., так как 
, то 
для каждого 
.
Теорема доказана.
Следствие 1.6 Квадратичная форма отрицательно определена тогда и только тогда, когда знаки определителей 
чередуются в такой последовательности:
,
Лекция "Тестовые задания" также может быть Вам полезна.
т.е., все определители с четными номерами положительны, а с нечетными отрицательны.
Доказательство. Упражнение.
Из доказанных результатов можно сделать вывод, что если не все определители положительны, но все отличны от нуля, и их знаки меняются в зависимости от номера иначе, чем указано в следствии 1.6, то рассматриваемая квадратичная форма является формой общего вида. При равенстве некоторых определителей нулю форма может быть полуопределенной, но, в частности, неотрицательности их всех не достаточно для положительной полуопределенности. Можно лишь утверждать, что необходимо и достаточно, чтобы какие-то из 
определителей были положительны. Можно доказать, что это требование равносильно требованию неотрицательности любого определителя вида:
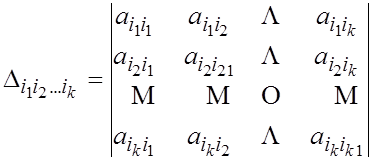
Мы, однако, не будем здесь строго даже формулировать матричный критерий полуопределнности квадратичной формы.
Критерий Сильвестра будет нашим основным инструментом при исследовании на экстремум функций нескольких переменных.
