Ответы и подсказки к упражнениям
Ответы и подсказки к упражнениям
Глава 3
3.1. В силу (3.2.5), имеем
E(ау)= =а
=а =аЕ(у).
=аЕ(у).
3.2. В силу (3.2.2), имеем
D(ау)=E[(аy–аy)2]=a2E[(y–y)2]=a2s2
3.3. В силу (3.2.9), имеем
С(yi, yj)=E[(yi–yi)(yj–yj)]=E(yiyj–yiyj–yiyj+yiyj)=E(yiyj)–yiE(yj)–E(yi)yj+yiyj=E(yiyj)–yiyj.
3.4. E(yiyj)= =
= [в силу (3.2.11)]
[в силу (3.2.11)]
Рекомендуемые материалы
= =E(yi)
=E(yi) =E(yi)Е(yj)
=E(yi)Е(yj)
3.5. В силу (3.2.10) и (3.2.12), С(yi, yj)=E(yiyj)–yiyj=yiyj–yiyj.
3.6. Е(х+у)=Е =
= =
=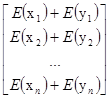
= +
+ =Е
=Е +Е
+Е .
.
3.7. D(y)=E[(y–y)(y–y)T]= E(yyT–yyT–yyT+yyT)
=E(yyT)–yE(yT)–E(y)yT+yyT
=E(yyT)–yyT–yyT+yyT
3.9. В силу (3.3.4), имеем
D(v)=С =E[(v–ω)(v–ω)T]=E
=E[(v–ω)(v–ω)T]=E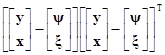
=E [(y–y)T(x–ξ)T]=E
[(y–y)T(x–ξ)T]=E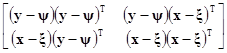
= =
= .
.
3.10. Пусть z= , K=
, K= , L=[I I O O] и M=[O O I I]. Тогда
, L=[I I O O] и M=[O O I I]. Тогда
С(Ay+Bx, Cv+Dw)=LKC(z)KTMT
=[A B O O]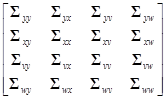
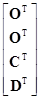
=AΣyvCT+BΣxvCT+AΣywDT+BΣxwDT
3.11.
- E(x) =8 и D(x) =2.
- E(x)=
![]() и C(x)=
и C(x)=![]() .
.
3.12.
- E(w)=
![]() и C(w)=
и C(w)=![]() .
. - С(x, w)=
![]() .
.
Глава 4
4.1. Используйте (3.2.1) и (3.2.2), а затем интегрирование.
4.2. Используя теорему П.15.1 и цепное правило дифференцирования (полагая, что можно поменять местами интегрирование и дифференцирование), получаем
 =exp(tTy)
=exp(tTy) =уexp(tTy),
=уexp(tTy),
 =
= =
= ,
,
 =
= =E(у) [в силу (3.2.1) и (3.3.1)].
=E(у) [в силу (3.2.1) и (3.3.1)].
4.3. Пусть K(t)=ln[М(t)]. Тогда  =
= и
и  =
= . А так как M(0)=1, то
. А так как M(0)=1, то  |t=0=s2 (см. раздел 5.2 после теоремы 5.2.2 и теорему 5.2.3).
|t=0=s2 (см. раздел 5.2 после теоремы 5.2.2 и теорему 5.2.3).
4.4. CSCT=CIs2CT=s2CCT=s2I. Используйте пункт 2 теоремы 4.5.2.
4.5. Используйте (П.3.1) и (П.3.2).
4.6. Представьте g(у) с помощью  и S=
и S= . Для det(A) и S–1 используйте (П.9.7) и (П.5.6). После сокращения h(у2) в (4.5.7) покажите, что f(у1|у2) может быть записана в виде
. Для det(A) и S–1 используйте (П.9.7) и (П.5.6). После сокращения h(у2) в (4.5.7) покажите, что f(у1|у2) может быть записана в виде
f(у1|у2) = ехр[–(у–y12)TS12–1(у–y12)/2],
ехр[–(у–y12)TS12–1(у–y12)/2],
где y12=y1+S12S22–1(у2–y2) и S12=S11–S12S22–1S21.
4.7.
1. Вектор  имеет распределение N2
имеет распределение N2 .
.
- y2 имеет распределение N(2, 6).
- x имеет распределение N(–4, 79).
- x=
![]() имеет распределение N2
имеет распределение N2![]() .
. - f(y1, y2|y3, y4)=N2
![]()
- E(y1, y3|y2, y4)=
![]() +
+![]()
![]()
![]() ,
,
C(y1, y3|y2, y4)=  –
–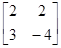
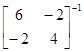
 . Следовательно,
. Следовательно,
f(y1, y3|y2, y4)=N2 .
.
- r13=–1/2
![]() .
. - r13-24=1/
![]() . Заметим, что r13-24 имеет противоположный знак по сравнению с r13.
. Заметим, что r13-24 имеет противоположный знак по сравнению с r13. - Используя разделение
y= и S=
и S= ,
,
имеем
Е(y1|y2, y3, y4)=1+[2 –1 2]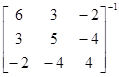
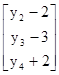
=1+[2 –1 2]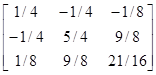
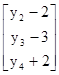
=y2/2+y3/2+5y4/4+1.
D(y1|y2, y3, y4)=4–[2 –1 2]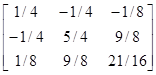
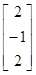
=4–3=1.
Отсюда, f(y1|y2, y3, y4)= N(1+y2/2+y3/2+5y4/4, 1).
4.8.
- N(17, 79).
- N2
![]() .
. - f(y2|y1, y3)=N(–5/2+y1/4+y3/3, 17/12).
- f(y1, y2|y3)=N2
![]() .
. - r12=
![]() /4 и r12-3=
/4 и r12-3=![]() .
.
4.9. Независимыми являются переменные y1 и y2, а также y2 и y3.
4.10. Независимыми являются переменные y1 и y2, а также векторы  и
и  .
.
Глава 5
5.1. (a) По теореме 5.2.3 получаем
D(s2)= D[уT(I–E/n)у]
D[уT(I–E/n)у]
= {2след[(I–E/n)s2I]2+4y2s21T(I–E/n)1}
{2след[(I–E/n)s2I]2+4y2s21T(I–E/n)1}
= [2s4след(I–E/n)+4y2s2(n–n)]=2s4/(n–1).
[2s4след(I–E/n)+4y2s2(n–n)]=2s4/(n–1).
(б) D(s2)=D =
= D(u)
D(u)
= 2(n–1)=
2(n–1)= .
.
5.2. уTAy =(y–y+y)TA(y–y+y)
=(y–y)TA(y–y)+(y–y)TAy+yTA(y–y)+yTAy
=(y–y)TA(y–y)+2(y–y)TAy+yTAy
5.3. (а)  =
=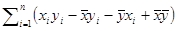
= –
–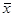
 –
–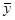
 +
+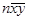
= –
–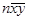 –
–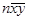 +
+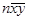 .
.
(б) При хT=[x1, x2, …, xn], yT=[y1, y2, …, yn], 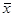 =1Tx/n и
=1Tx/n и 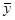 =1Ty/n, имеем
=1Ty/n, имеем
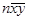 =n1Tx1Ty/n2=xT11Ty/n=xTЕy/n,
=n1Tx1Ty/n2=xT11Ty/n=xTЕy/n,
 –
–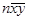 =xTЕy–xTЕy/n=xT(I–Е/n)y.
=xTЕy–xTЕy/n=xT(I–Е/n)y.
5.4. В силу (5.2.6), D(yТAy)=2след[(AS)2]+4yTASAy. В данном случае ищется D(v)=D(yТy), где y имеет распределение Nn(y, I). Следовательно, А=S=I и
D(yТy)=2след(I2)+4yTy=2n+8g,
так как I размеров пхп, след(I)=п и 4yTy=8g, в силу g =yTy/2.
5.5. ln[Mv(t)]= –(n/2)ln(1–2t)–g [1–(1–2t)–1],
d{ln[Mv(t)]}/dt =n/(1–2t)–g [1–2(1–2t)–2],
d{ln[Mv(0)]}/dt = n+2g,
d2{ln[Mv(t)]}/dt2= n/(1–2t)2–8g (1–2t)–3,
d2{ln[Mv(0)]}/dt2=2n+8g.
5.6. По теореме 5.5 квадратичная форма (у–y)Т S–1(у–y) имеет распределение c2(n), так как АS=S–1S =I (которая идемпотентная) и Е(у–y)=0. Квадратичная форма уТ S–1у имеет распределение c2(n, g), где g =yТS–1y/2.
5.8. 1T(I–Е/n)=1T(I–11T/n)=1T–1T11T/n=1T–n1T/n=0T.
5.9.
- Используйте пункт 1 теоремы 4.5.2. В этом случае, а=1/n.
- t= tу/
![]() =
=![]() . Покажите, что tу=(
. Покажите, что tу=(![]() –y)/(
–y)/(![]() ) имеет распределение N(0, 1).
) имеет распределение N(0, 1). - Пусть t0=(
![]() –y0)/(
–y0)/(![]() ). Тогда Е(t0)= (y –y0)/(
). Тогда Е(t0)= (y –y0)/(![]() )=d и D(t0)=[1/(s2/n)]D(
)=d и D(t0)=[1/(s2/n)]D(![]() )=1. Следовательно, t0 имеет распределение N(d, 1) и, в силу (5.4.2), получаем, что
)=1. Следовательно, t0 имеет распределение N(d, 1) и, в силу (5.4.2), получаем, что
 =
= имеет распределение t(n–1, d).
имеет распределение t(n–1, d).
Отсюда d =(y –y0)/( ).
).
5.10. В разделе 5.1 показано, что матрицы I–Е/n и Е/n идемпотентные и (I–Е/n)(Е/n)=O. В примере 5.5 найдено, что  =yТ(I–E/n)y/s2 имеет распределение c2(n–1). Покажите, что п
=yТ(I–E/n)y/s2 имеет распределение c2(n–1). Покажите, что п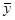 2/s2=yТ(E/n)y/s2 имеет распределение c2(1, g), где g=yTAy/2 =пy2/2s2. Так как (I–Е/n)(Е/n)=O то квадратичные формы yТ(E/n)y и yТ(I–E/n)y независимы. Отсюда, в силу (5.4.3), п
2/s2=yТ(E/n)y/s2 имеет распределение c2(1, g), где g=yTAy/2 =пy2/2s2. Так как (I–Е/n)(Е/n)=O то квадратичные формы yТ(E/n)y и yТ(I–E/n)y независимы. Отсюда, в силу (5.4.3), п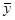 2/[
2/[ ] имеет распределение F(1, n–1, g), где g= пy2/2s2. Если y=0 (Н0 верна), то g=0 и п
] имеет распределение F(1, n–1, g), где g= пy2/2s2. Если y=0 (Н0 верна), то g=0 и п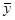 2/[
2/[ ] имеет распределение F(1, n–1).
] имеет распределение F(1, n–1).
5.11.
2. Так как
 =yТ(I–E/n)y/[s2(1–r)]=yТ{A/[s2(1–r)]}y
=yТ(I–E/n)y/[s2(1–r)]=yТ{A/[s2(1–r)]}y
имеем
AS/[s2(1–r)]=s2/[s2(1–r)]=(I–E/n)[(1–r)I+rЕ].
Покажите, что это равно идемпотентной матрице (I–E/n).
5.12.
1. E(уTAy)=след(AS)+yTAy=–16.
2. D(уTAy)=2след(AS)2+4yTASAy=21 138.
3. Проверьте, является ли матрица AS идемпотентной.
4. Проверьте, является ли матрица A идемпотентной.
5.13. A=S–1=диаг(1/2, 1/4, 1/3), yTAy/2=2,9167.
5.14. A=S–1, yTAy/2=27.
5.15.
1. Покажите, что матрица A идемпотентная и имеет ранг 2 равный след(А). Поэтому уTAy/s2 имеет распределение c2[n, yТAy/(2s2)], где yТAy/2=12,6/2=6,3.
2. BA= ≠O. Поэтому уTAy и Ву не являются независимыми.
≠O. Поэтому уTAy и Ву не являются независимыми.
3. y1+y2+y3=1Tу. Покажите, что 1TA=0T. Поэтому уTAy и y1+y2+y3 являются независимыми.
5.16.
- Покажите, что В идемпотентная ранга 1. Следовательно, уTВy/s2 имеет распределение c2[1, yТВy/(2s2)]. Найдите yТВy/2.
- Покажите, что ВА=О. Следовательно, уTВy и уTAy независимы.
5.17.
- H2=X(XTX)–1XTX(XTX)–1XT=X(XTX)–1XT=H. По теореме П.13d ранг(H)=след(H) =след[X(XTX)–1XT]. По пункту 2 теоремы П.11 получаем след[X(XTX)–1XT] =след(Iр) =р. Так же и след(I–H)=п–р.
- след(Hs2I) =след(s2X(XTX)–1XT)=рs2. yTHy=(Xb)TX(XTX)–1XT(Xb)=bTXTXb. Поэтому E(уTHy)= рs2+bTXTXb. Покажите, что след[(I–H)Is2]=(п–р)s2 и, если y=Xb, то yT(I–H)y=0. Следовательно, E[уT(I–H)y]=(п–р)s2.
- уTHy/s2 имеет распределение c2(р, g), где g=yТHy/(2s2)=bTXTXb/(2s2). Квадратичная форма уT(I–H)y/s2 имеет распределение c2(п–р).
- Покажите, что X(XTX)–1XT[I–X(XTX)–1XT]=О. Тогда по следствию 1 теоремы 5.6.2 уTHy и уT(I–H)y независимы.
- Распределение F(р, n–р, g), где g=bTXTXb/(2s2).
Глава 6
6.1.
![]() =–1434,544+57,38x. Заметим, что –1434,544 достигается при x=0, далеко за пределами рассматриваемых данных, и не имеет практического значения.
=–1434,544+57,38x. Заметим, что –1434,544 достигается при x=0, далеко за пределами рассматриваемых данных, и не имеет практического значения.- x0 =25,10 и S=0,05.
![]() =5,694+2,869x. Результат оценки ожидаемых значений переменной (у) и остатки те же, что и в пункте 1.
=5,694+2,869x. Результат оценки ожидаемых значений переменной (у) и остатки те же, что и в пункте 1.- При подстановке x=(x–25,1)/0,05 в модель у=b0+b1x+e она превращается в модель у=b0+b1x +e. Поэтому модели идентичны.
- Суммирующиеся в нуль остатки 1,594, –0,465, –1,764, –1,453, 2,088 показывают кривизну относительно аппроксимирующей прямой, что видно из графического представления. В этом случае необходимо преобразование переменной (у) или использование в модели члена х2.
![]() =0,6281+0,2360x.
=0,6281+0,2360x.
| x | у |
| e=y– | |
| –2 | 0,1903 | 0,1561 | 0,0342 | |
| –1 | 0,3729 | 0,3921 | –0,0192 | |
| 0 | 0,5944 | 0,6281 | –0,0337 | |
| 1 | 0,8519 | 0,8641 | –0,0122 | |
| 2 | 1,1310 | 1,1001 | 0,0309 | |
| 0 | 3,1405 | 3,1405 | 0,0 | Суммы |
| 10 | 2,533474= | 2,529508+ | 0,003778 | Суммы квадратов |
(Равенство сумм квадратов имеет ошибку округления 0,000188.) Логарифмическое преобразование не устраняет кривизны.
- В дополнение к столбцам в пункте 6 необходимы следующие столбцы, где h0=0,6+0,25x.
| h0 | y–h0 |
| |
| 0,10 | 0.0903 | 0,0561 | |
| 0,35 | 0,0229 | 0,0421 | |
| 0,60 | -0.0056 | 0,0281 | |
| 0,85 | 0,0019 | 0,0141 | |
| 1,10 | 0,0310 | 0,0001 | |
| 3,0 | 0,1405 | 0,1405 | Сумма |
| 96,74х104 | 59,08х104 | Суммы квадратов |
| Источник вариаций | Суммы квадратов | Степени свободы | Средние квадратичные | FH |
| Модель | S( | 2 | 29,54 | 2,346 |
| Остатки | S(y– | 3 | 12,59 | |
| Итого | S(y–h0)2=96,74 х104 | 5 |
Гипотеза Н0: b0=0,6, b1=0,25 верна при α=0,10. (В колонке Суммы квадратов виден эффект ошибки округления.)
6.2.
b=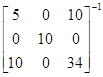
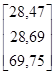 =
=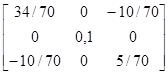
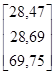
 =3,864+2,869x+0,915x2.
=3,864+2,869x+0,915x2.
| y |
| e=y– |
| 1,55 | 1,786 | –0,236 |
| 2,36 | 1,910 | 0,450 |
| 3,93 | 3,864 | 0,066 |
| 7,11 | 7,648 | –0,538 |
| 13,52 | 13,262 | 0,258 |
Модель у=b0+b1x+b2x2+e имеет дополнительный параметр, но остатки менее систематичны.
6.3.  =(Sx2)–1(Sxy)=5–145=9, h0=8.
=(Sx2)–1(Sxy)=5–145=9, h0=8.
S( –h0)2=5, S(y–
–h0)2=5, S(y– )2=10, FH=(5/1)/(10/4)=2,0.
)2=10, FH=(5/1)/(10/4)=2,0.
Pr[F(1, 4)>2,0] больше 0,10 поэтому гипотеза H0 верна.
6.4.
- х=(x–30)/12.
![]() =9,471–6,3500х.
=9,471–6,3500х.
| Источники вариаций | Суммы квадратов | Степени свободы | Средние квадратичные | FH |
| b0 | 1255,91 | 1 | ||
| b1│b0 | 1209,67 | 1 | ||
| Неадекватность | 374,15 | 3 | 124,73 | 186,1 |
| Чистые ошибки | 6,07 | 9 | 0,67 | |
| Итого | 2845,80 | 14 |
Ясно показана неадекватность. Остатки показывают кривизну. Другие возможные модели: у=b0+b1x+b11x2+e и w=ln(y)=b0+b1x+e.
![]() =3,326–6,3500x+2,8678x2.
=3,326–6,3500x+2,8678x2.
 =1,5219–0,86634x.
=1,5219–0,86634x.
Остатки для первого уравнения при увеличении (х) получаются в виде трёх плюсов, трёх минусов, пяти плюсов и трёх минусов, то есть показывают систематическое отклонение от используемой модели. Второе уравнение, похоже, предпочтительно.
- Это обнаружение наводит на мысль об автокорреляции между значениями переменной (у) в столбцах таблицы, что требует оценки корреляций и использования обобщённого метода наименьших квадратов или другого анализа.
6.5. Результаты смещения оценок следуют из применения формулы Е(b)=b+Аb2, где
Х= , Х=
, Х= , ХTХ=
, ХTХ= , ХTХ2=
, ХTХ2= , А=(ХTХ)–1ХTХ2.
, А=(ХTХ)–1ХTХ2.
- Нет. Если это так, то с2=
![]() d и d=
d и d=![]() с, означая, что с=
с, означая, что с=![]() 2 получаемое подстановкой второго требуемого условия в первое. Отсюда должно бы удовлетворяться условие с–
2 получаемое подстановкой второго требуемого условия в первое. Отсюда должно бы удовлетворяться условие с–![]() 2=0. В нём левая часть представляет сумму квадратов значений переменной х относительно их среднего, что равно нулю только, если все значения х одинаковы, давая бесполезный план только с одним уровнем переменной х, который нельзя использовать для решения модели.
2=0. В нём левая часть представляет сумму квадратов значений переменной х относительно их среднего, что равно нулю только, если все значения х одинаковы, давая бесполезный план только с одним уровнем переменной х, который нельзя использовать для решения модели. - Да. Любой симметричный относительно нуля план имеет
![]() =d=0. Например, любой трёхуровневый план с п1, п2 и п3 наблюдениями соответственно при х= –1, 0 и 1, будет иметь это свойство. Для таких планов Е(b0)=b0+сb11 и Е(b1)=b1.
=d=0. Например, любой трёхуровневый план с п1, п2 и п3 наблюдениями соответственно при х= –1, 0 и 1, будет иметь это свойство. Для таких планов Е(b0)=b0+сb11 и Е(b1)=b1.
6.7. Для проверки гипотезы H0: b1=с в сравнении с H1: b1≠с используйте статистику
tH=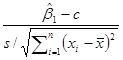
и отклоните H0, если │tH│≥tα/2(n–2). Покажите, что tH имеет распределение t(n–2, d), где
d= .
.
6.8. (а) Для проверки гипотезы H0: b0=а в сравнении с H1: b0≠а используйте статистику
tH=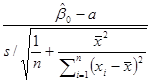
и отклоните H0, если │tH│≥tα/2(n–2). Покажите, что tH имеет распределение t(n–2, d), где
d= .
.
(б) 100(1–α)% доверительный интервал для b0 получается в виде
±stα/2(n–2) .
.
Глава 7
7.1. В силу (П.2.10), q0+q1xi1+q2xi2+…+qр–1xiр–1=xiсТq. В силу (П.2.12) и (П.2.19), получаем
 =[y1–
=[y1– , y1–
, y1– , …, y1–
, …, y1– ,]
,]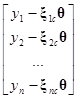
=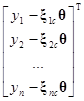
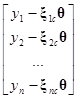 =(у–Xq)Т(у–Xq).
=(у–Xq)Т(у–Xq).
7.2. Умножьте (7.2.6) используя (П.2.9). Держите у–Xq вместе и Xq–Xq вместе. Вынесите X за скобки в Xq–Xq.
7.4. Начиная с (6.2.13), имеем
D( )=s2
)=s2 =s2
=s2 =s2
=s2 .
.
7.5. Два недостающих члена в (7.2.13) следующие
[А–(XТX)–1XТ][(XTX)–1XТ]Т+(XTX)–1XТ][А–(XТX)–1XТ]Т.
Учитывая, что AX=I, первое принимает значение
АX(XTX)–1–(XТX)–1XТX(XTX)–1=(XX)–1–(XТX)–1=О.
7.6. Чтобы сделать дисперсию D(сТу) минимальной, при условии сТX=aТ, возьмём производные от v=s2cТc–(сТX–aТ)l по с и l (см. раздел П.14 о минимизации функции вектора):
 =–XТс+a=0 даёт а=XТс и
=–XТс+a=0 даёт а=XТс и  =2s2c–Xl=0 даёт с=Xl/(2s2).
=2s2c–Xl=0 даёт с=Xl/(2s2).
Подставляя с=Xl/(2s2) в а=XТс, получаем а=XТXl/(2s2) или l=2s2(XX)–1а. Отсюда с=Xl/(2s2)=X(XX)–1а.
7.7.  =(FТF)–1FТy=(KТXТXK)–1KТXТy=K–1(XТX)–1(KТ)–1KТXТy=K–1(XТX)–1XТy=K–1
=(FТF)–1FТy=(KТXТXK)–1KТXТy=K–1(XТX)–1(KТ)–1KТXТy=K–1(XТX)–1XТy=K–1 .
.
7.8. (у–X )Т(у–X
)Т(у–X )=уТу–уТX
)=уТу–уТX –
– ТXТу+
ТXТу+ ТXТX
ТXТX . Используйте (7.2.5).
. Используйте (7.2.5).
7.9. В силу (7.2.5),  Т(XТу)=
Т(XТу)= Т(XТX
Т(XТX ). По теореме 5.2.1 Е(уТу)= Е(уТIу)=след(Is2I)+Е(уТ)IЕ(у)=пs2+qТXТXq. По теоремам 7.2.2 и 7.2.3 E(
). По теореме 5.2.1 Е(уТу)= Е(уТIу)=след(Is2I)+Е(уТ)IЕ(у)=пs2+qТXТXq. По теоремам 7.2.2 и 7.2.3 E( )=q и С(
)=q и С( )=s2(XТX)–1. Следовательно, Е(
)=s2(XТX)–1. Следовательно, Е( ТXТX
ТXТX )= след[(XТX)s2(XТX)–1]+qТXТXq.
)= след[(XТX)s2(XТX)–1]+qТXТXq.
7.11. Сначала покажите, что 1ТX1/п=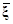 , где
, где 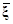 =[
=[ ,
,  , …,
, …,  ] состоит из усреднённых столбцов матрицы X1. Затем
] состоит из усреднённых столбцов матрицы X1. Затем
(I–E/n)X1=X1–EX1/n=X1–11ТX1/n=X1–1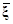
= –
– .
.
7.12. Используя (П.5.6) при А11=п, А12=п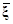 Т, А21=п
Т, А21=п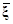 , А22=X1ТX1 и XcТXc=X1ТX1–п
, А22=X1ТX1 и XcТXc=X1ТX1–п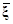
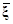 Т, покажите, что
Т, покажите, что
(XТX)–1= =
= =
=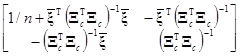
и проверьте умножением, что (XТX)–1XТX=I. При таком разделении матрицы (XТX)–1 покажите, что
 =(XТX)–1XТy={[1, X1]T[1, X1]}–1
=(XТX)–1XТy={[1, X1]T[1, X1]}–1 =
= =
= ,
,
что то же самое, как в (7.5.12) и (7.5.13).
7.13. Два опущенные члена в (7.3.12) следующие
–(у–X )ТX(
)ТX( –q)–(
–q)–( –q)ТX(у–X
–q)ТX(у–X )=–(XТу–XТX
)=–(XТу–XТX )Т(
)Т( –q)–(
–q)–( –q)Т(Xу–XX
–q)Т(Xу–XX )
)
=–0Т( –q)–(
–q)–( –q)Т0,
–q)Т0,
так как XТу–XТX =0 в силу нормальных уравнений.
=0 в силу нормальных уравнений.
7.15. Покажите, что Е2=пЕ. Затем умножьте V на V–1 чтобы получить I, где V и V–1 даны соответственно в (7.5.19) и (7.5.20).
7.16. (а) 1ТV–11=а1Т(I–brЕ)1=а1Т1–аbr1Т11Т1=ап–аbrп2=ап(1–brп). Подставьте вместо а и b их выражения чтобы показать, что это равно п/[1+(n–1)r]=bп. Затем 1ТV–1Xc= а1Т(I–brЕ)Xc= а1ТXc– аbr1Т11ТXc=0Т, так как 1ТXc=0Т. Покажите, что
XcТV–1Xc=аXcТXc.
7.17. С( )=(XТX)–1XТС(у)X(XТX)–1=sк2(XТX)–1XТVX(XТX)–1.
)=(XТX)–1XТС(у)X(XТX)–1=sк2(XТX)–1XТVX(XТX)–1.
7.18. (а)  =(XТV–1X)–1XТV–1y=
=(XТV–1X)–1XТV–1y=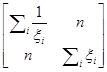
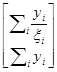
=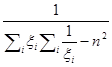
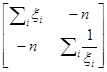
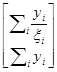 .
.
7.20. (а) D[ /
/ ]=
]= D(yi)/
D(yi)/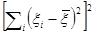
= /
/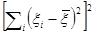 .
.
Глава 8
8.1. С( ) =E{[
) =E{[ –E(
–E( )][(
)][( –E(
–E( )]T}. В силу (8.2.4), Е(
)]T}. В силу (8.2.4), Е( )=b1+Аb2, имеем
)=b1+Аb2, имеем
 –E(
–E( )=
)= –b1–Аb2=
–b1–Аb2= –b1–(X1ТX1)–1X1ТX2b2
–b1–(X1ТX1)–1X1ТX2b2
=(X1ТX1)–1X1Ту–(X1ТX1)–1X1ТX2b2–b1
=(X1ТX1)–1X1Т(у–X2b2)–b1.
Покажите, что это можно записать в виде (X1ТX1)–1X1Т(у–X1b1–X2b2), так что
С( ) = E[(X1ТX1)–1X1Т(у–Xb)(у–Xb)ТX1(X1ТX1)–1].
) = E[(X1ТX1)–1X1Т(у–Xb)(у–Xb)ТX1(X1ТX1)–1].
8.2. E(x01с )=x01с(b1+Аb2) ≠ x01сb1.
)=x01с(b1+Аb2) ≠ x01сb1.
8.3. D(x01с ) ≥ D(x01с
) ≥ D(x01с )
)
=s2(x01сG11x01сТ–x01сG11–1x01сТ)
=s2x01с(G11–G11–1)x01сТ
≥ 0, так как матрица G11–G11–1=АВ–1А положительно определённая (см. пункт 2 теоремы 8.2.3)
8.4. Возьмём производную  =0, тогда 2
=0, тогда 2 =0.
=0.
8.5. Для адекватной модели уi=b0+b1xi +ei имеем
Х= ,
,
а для неадекватной модели уi=b1*xi +ei* имеем Х1T= [x1, x2, …, xn]. Поэтому Х2T= [1, 1, …, 1]. Тогда, в силу (8.2.4), получаем
E( )=b1+Аb2=b1+(X1ТX1)–1X1ТX2b2
)=b1+Аb2=b1+(X1ТX1)–1X1ТX2b2
=b1+b2 .
.
8.6. (а)
X= .
.
Первые два столбца составляют матрицу Х1, а последние два столбца являются матрицей Х2. Тогда, в силу (8.2.4), имеем
E( )=b1+Аb2=b1+(X1ТX1)–1X1ТX2b2.
)=b1+Аb2=b1+(X1ТX1)–1X1ТX2b2.
Покажите, что отсюда
E( )=
)= +
+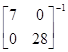
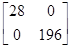
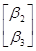
= +
+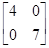
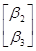 ,
,
так что E( )=b0+4b2 и E(
)=b0+4b2 и E( )=b1+7b3.
)=b1+7b3.
8.7. X1TXО=X1T[Х2–Х1(X1ТX1)–1X1ТX2]=X1TХ2–X1TХ1(X1ТX1)–1X1ТX2]=O.
8.8. d(h–h2)/dh=1–2h=0, отсюда h=1/2, следовательно, 1/2–(1/2)2=1/4.
Глава 9
9.1. Hc[I–Е/n]=Hc–HcЕ/n=Xc(XcТXc)–1XcТ–Xc(XcТXc)–1XcТ 11Т/n= Xc(XcТXc)–1XcТ–О, так как XcТ11Т=О1Т=О.
9.3. Большинство требуемого здесь получено в упражнении 5.17.
9.4. HH1=X(XТX)–1XТX1(X1ТX1)–1X1Т=X1(X1ТX1)–1X1Т=H1.
9.6. s2+bр–12[xр–1Txр–1–xр–1TX1(X1ТX1)–1X1Тxр–1].
9.7. После умножения получаются восемь членов, в которых три из первых четырёх сокращаются с тремя из последних четырёх. Например, из последних четырёх второй  ТX1ТX1А
ТX1ТX1А =
= ТX1ТX1X1(X1ТX1)–1X1ТX2
ТX1ТX1X1(X1ТX1)–1X1ТX2 =
= ТX1ТX2
ТX1ТX2 такой же, как и второй из первых четырёх.
такой же, как и второй из первых четырёх.
9.8. Здесь можно применить теорему 9.3.4. Используйте аТ=[0, …, 0, 1] вместо С в (9.3.8) чтобы получить
 =
=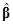 –(XТX)–1а[аТ(XТX)–1а]–1аТ
–(XТX)–1а[аТ(XТX)–1а]–1аТ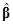
=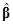 –(XТX)–1ааТ
–(XТX)–1ааТ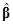 /gjj.
/gjj.
В силу (П.3.3), (XТX)–1а является линейной комбинацией столбцов матрицы (XТX)–1. Следовательно,  =
=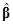 –gj
–gj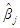 /gjj, где gjj - j-й диагональный элемент матрицы (XТX)–1 и gj - j-й столбец матрицы (XТX)–1. Подставляя выражение для
/gjj, где gjj - j-й диагональный элемент матрицы (XТX)–1 и gj - j-й столбец матрицы (XТX)–1. Подставляя выражение для  в
в 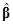 ТXТy–
ТXТy– ТX1Тy получаем
ТX1Тy получаем
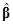 ТXТy–
ТXТy– ТX1Тy=
ТX1Тy=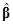 ТXТy–(
ТXТy–(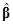 ТX1Тy–gjТX1Тy
ТX1Тy–gjТX1Тy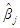 /gjj)=
/gjj)=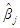
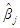 /gjj,
/gjj,
так как gjТX1Тy является j-м элементом 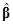 .
.
9.9. Pr[tα/2(п–р)≤ ≤tα/2(п–р)]=1–α
≤tα/2(п–р)]=1–α
Решите неравенство относительно aTb.
9.10. Е(y0– )=Е(y0–x0с
)=Е(y0–x0с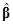 )=x0сb–x0сb=0. В силу (9.5.8), D(y0–
)=x0сb–x0сb=0. В силу (9.5.8), D(y0– )=s2[1+x0с(XТX)–1x0сТ]. По пункту 1 теоремы 7.3.4 и пункту 1 теоремы 4.5.2, (y0–
)=s2[1+x0с(XТX)–1x0сТ]. По пункту 1 теоремы 7.3.4 и пункту 1 теоремы 4.5.2, (y0– )/{s2[1+x0с(XТX)–1x0сТ]}1/2 имеет распределение N(0, 1). По пункту 2 теоремы 7.3.4, (п–р)s2/s2 имеет распределение c2(п–р). По пункту 3 теоремы 7.3.4 величины
)/{s2[1+x0с(XТX)–1x0сТ]}1/2 имеет распределение N(0, 1). По пункту 2 теоремы 7.3.4, (п–р)s2/s2 имеет распределение c2(п–р). По пункту 3 теоремы 7.3.4 величины  и s2 независимы. Используйте (5.4.6) чтобы показать, что tу=
и s2 независимы. Используйте (5.4.6) чтобы показать, что tу= имеет распределение t(п–р).
имеет распределение t(п–р).
9.11. 1. Покажите, что Е( –
– )=Е(
)=Е( –x0с
–x0с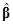 )=0 и D(
)=0 и D( –
– )=s2[1/q+x0с(XТX)–1x0сТ]. В остальном следуйте как в ответе к предыдущему упражнению.
)=s2[1/q+x0с(XТX)–1x0сТ]. В остальном следуйте как в ответе к предыдущему упражнению.
9.12. Инвертируйте (возьмите обратные) все три числа неравенства (что меняет направления этих двух неравенств) и умножьте на (п–р)s2.
Глава 10
Ответы к упражнениям даны после них в тексте главы.
Глава 11
11.1. Единственно реальным результатом оценки является D=66,7. Построение вновь графика кумулятивных вероятностей распределения для остальных результатов оценки дает стандартную ошибку (воздействия) =8, то есть,  =8х161/2/2=16 для оцениваемого стандартного отклонения отдельных наблюдений.
=8х161/2/2=16 для оцениваемого стандартного отклонения отдельных наблюдений.
11.2. (а) Результат оценки воздействия фактора находится по формуле: Результат оценки = (сумма значений отклика на верхнем уровне фактора минус сумма значений отклика на нижнем уровне фактора)/2k–1, а результат оценки коэффициента регрессии фактора b=(то же самое)/2k.
(б) Результат оценки воздействия от взаимодействия факторов находится по формулам (11.2.6) - (11.2.8) с делителем 2k–1, а формула оценки коэффициента регрессии взаимодействия имеет в числителе то же самое, а в знаменателе 2k.
11.3. Сначала добавим столбец 1 и определим четыре столбца матрицы модели Х как столбцы [1, х1, х2, х3]. Один столбец х4 определяется элементами, показанными в таблице. Применяя формулу Е(b) =β+(XTX)–1XTх4β4, где βT=[β0, β1, β2, β3], β4=β4 и b – вектор оценки вектора β параметров модели, то находим (XTX)–1XTх4= [0, 2, 3, –2]T и b0 является несмещённым, пока Е(b1)=β1+2β4, Е(b2)=β2+3β4, Е(b3)=β3–2β4.
11.4. (а) х1=(С% –0,5)/0,4; х2=(Mn% –0,8)/0,6; х3=(Ni% –0,15)/0,05.
(в) 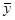 =552,5; А= –575; В=–90; С= –65; АВ=10; АС=15; ВС=10 и АВС=–10.
=552,5; А= –575; В=–90; С= –65; АВ=10; АС=15; ВС=10 и АВС=–10.
(г) D(результата оценки воздействия) =4s2/п=4 (65)2/8 =45,9622, так что стандартная ошибка результата оценки воздействия равна примерно 46. Только 1 результат оценки выходит за пределы интервала ±2(46)= ±92.
(д) Результат оценки воздействия фактора х1 отрицательный, так что повышение уровня C% снижает начальную температуру.
11.5. При нормировании х1=(ξ1–85)/25, х2= (ξ2–1760)/750, х3= (ξ3–4,65)/2,65, план узнаваем, как повторённый по плану 23 эксперимент с опытами [±1, ±1, ±1]. Значит 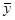 =29,59375 и результаты оценки факторных воздействий, округленные до двух знаков после запятой, следующие: А=15,01, В=11,73, С=9,54, АВ=0,06, АС=–0,69, ВС=1,34, АВС= –1,09, каждый с дисперсией 4s2/16=s2/4. Дисперсия s2 оценивается на основе повторных опытов. Каждая пара, например, 12,2 и 12,5 для опытов (–1, –1, –1), даёт 1 степень свободы для оценки s2 по специальной формуле для пары повторных опытов, например, (12,2–12,5)2/2=0,045. Восемь таких оценок могут быть усреднены и получено s2=1,8081 на основе 8 степеней свободы. [Помните, что в общем, средневзвешенная усреднённая (v1s12+v2s22+…+vrsr2)/(v1+v2+…+vr) является необходимой, но здесь все индивидуальные степени свободы равны 1, так что в этом случае общая формула подразумевает простое усреднение.] Стандартная ошибка результата оценки воздействия равна (1,8081/4)1/2=0,672 и только три главных воздействия являются существенными. Все положительные, так что увеличение ξ1, ξ2, ξ3 приведет к увеличению скорости врезания. Однако в сверлении есть и другие отклики для рассмотрения, такие как износ сверла и, как следствие, общая стоимость последовательности работ по сверлению. Таким образом, повышение уровней факторов позволит улучшить отклик, но это не обязательно лучшая практика. Необходима дополнительная информация, чтобы определить это. См., например, [Wu S.M. Tool life testing by response surface methodology, J. Engineering Industry, Trans. ASME, B-86, 1964, 105-116].
=29,59375 и результаты оценки факторных воздействий, округленные до двух знаков после запятой, следующие: А=15,01, В=11,73, С=9,54, АВ=0,06, АС=–0,69, ВС=1,34, АВС= –1,09, каждый с дисперсией 4s2/16=s2/4. Дисперсия s2 оценивается на основе повторных опытов. Каждая пара, например, 12,2 и 12,5 для опытов (–1, –1, –1), даёт 1 степень свободы для оценки s2 по специальной формуле для пары повторных опытов, например, (12,2–12,5)2/2=0,045. Восемь таких оценок могут быть усреднены и получено s2=1,8081 на основе 8 степеней свободы. [Помните, что в общем, средневзвешенная усреднённая (v1s12+v2s22+…+vrsr2)/(v1+v2+…+vr) является необходимой, но здесь все индивидуальные степени свободы равны 1, так что в этом случае общая формула подразумевает простое усреднение.] Стандартная ошибка результата оценки воздействия равна (1,8081/4)1/2=0,672 и только три главных воздействия являются существенными. Все положительные, так что увеличение ξ1, ξ2, ξ3 приведет к увеличению скорости врезания. Однако в сверлении есть и другие отклики для рассмотрения, такие как износ сверла и, как следствие, общая стоимость последовательности работ по сверлению. Таким образом, повышение уровней факторов позволит улучшить отклик, но это не обязательно лучшая практика. Необходима дополнительная информация, чтобы определить это. См., например, [Wu S.M. Tool life testing by response surface methodology, J. Engineering Industry, Trans. ASME, B-86, 1964, 105-116].
11.6. Результаты 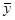 =4,071, А=2.99, В= –0,06, С= –1,93, АВ= –0,14, АС= –1,08, ВС=0,04, АВС= –0,11, se2=16,06=1,004. Стандартная ошибка воздействий равна 4se2/24 =0,41, так что результаты А, С и АС оценки все превышают 2 стандартные ошибки. Данные средних значений из шести наблюдений для факторов х1 и х3 можно предстатвить в таблице:
=4,071, А=2.99, В= –0,06, С= –1,93, АВ= –0,14, АС= –1,08, ВС=0,04, АВС= –0,11, se2=16,06=1,004. Стандартная ошибка воздействий равна 4se2/24 =0,41, так что результаты А, С и АС оценки все превышают 2 стандартные ошибки. Данные средних значений из шести наблюдений для факторов х1 и х3 можно предстатвить в таблице:
| х3 | 2,15 | 4,07 |
| 3 | 7,07 | |
| х1 |
Повышенная прочность на разрыв явно достигнута при +1 бумаги (х1), но прочность на разрыв сильно зависит от направления разрыва (х3).
11.7.  =29,594–7,506х1+5,869х2+4,769х3.
=29,594–7,506х1+5,869х2+4,769х3.
| Источники вариаций | Суммы квадратов | Степени свободы | Средние квадратичные | Статистика F |
|
| 14012,64 | 1 | - | |
|
| 901,50 | 1 | 901,50 | 382,80 |
|
| 551,08 | 1 | 551,08 | 234,00 |
|
| 363,85 | 1 | 363,85 | 154,50 |
| Неадекватность | 13,79 | 4 | 3,448 | 1,906 |
| Чистые ошибки | 14,47 | 8 | 1,809 | |
| Итого | 15857,33 | 16 |
Заметим, что  0=
0=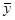 и
и  в два раза меньше результатов оценки факторных воздействий.
в два раза меньше результатов оценки факторных воздействий.
Модель адекватная, так что s2= (13,79 +14,47)/(4+8) =2,355 является результатом оценки s2. Результаты оценки коэффициентов регрессии  ,
,  и
и  являются в высшей степени значимыми.
являются в высшей степени значимыми.
11.8. Два из факторов, х1 - тип бумаги и х3 - направление разрыва, нечисловые и, как правило, не могут быть подходяще экстраполированы или интерполированы. Только числовой фактор, х2 - влажность, мало влияет на отклик.
11.9. Частичный ответ дан после упражнения.
11.10. Регрессионная версии результатов оценки воздействий факторов (половины результатов оценки воздействий факторов): 218,75, –14,25 и –10, результататы оценки воздействий соответствующих двухфакторных взаимодействий: –15,25, –20 и 15,5; а результат оценка воздействия трёхфакторного взаимодействия: 16. Хотя и нет значения ошибки для сравнения с этими результатами оценки, понятно, что только результат оценки воздействия фактора х1 сравнительно большой, а остальное все можно расценить как остаточные изменения. С точки зрения времени разряда, батареи высокой стоимости кажутся стоящими, в то время как тип разъема и температура батареи оказывают небольшое воздействие.
Глава 12
12.1. (а) Истинно. Наибольшее значение R определяется половинной фракцией с генерирующими равенствами 1=±х1◦х2◦...◦хq, так что R не может превысить q. Например, план 2III3–1 с определяющим отношением 1=х1◦х2◦х3 имеет q=R=3.
(б) Ложно. Например, план 2III3–1 с определяющим отношением 1=х1◦х2◦х3 имеет q=3, R=3 и k=1, так что 3=q <R+k=4.
12.2. (а) Положим, что все воздействия взаимодействий между факторами x1, x2 и x3 равны нулю, как и воздействия взаимодействий между факторами x3, x4 и x5. Определяющим отношением является 1=х1◦х2◦х3◦х4 =х1◦х3◦х5=х2◦х4◦х5. Игнорируя воздействия от взаимодействий трех или более факторов, можно оценить
Среднее (AB)+(CD)
A+(CE) (AC)+BD+E
B+(DE) (BC)+AD
C+AE (ABC) +D+BE
Два воздействия факторов не совмещены, а три совмещены. (Воздействия в круглых скобках полагаются равными нулю, но перечислены для информации.)
(б) Лучше план с определяющим отношением 1=х1◦х2◦х3=х3◦х4◦х5 (=х1◦х2◦х4◦х5). С его использованием можно оценить
Среднее D+(CE)
A+(BC) E+(CD)
B+(AC) AD+BE
C+(AB)+(DE) BD+AE
Здесь, ввиду предположений, все пять воздействий факторов не совмещены с воздействиями двухфакторные взаимодействия и четыре воздействия двухфакторных взаимодействий совмещены в две пары.
12.3. План (а) имеет 1=х1, в то время как план (б) разрешающей способности III. Таким образом, (б) значительно лучше.
12.4. (а) Первая фракция имеет определяющее отношение 1=х8=х1◦х2◦х3◦х4 =х1◦х2◦х5 =х1◦х4◦х6 =х2◦х4◦х7. Фракция, полученная изменением знаков на обратные, имеет определяющее отношение 1=–х8=х1◦х2◦х3◦х4 =–х1◦х2◦х5 =–х1◦х4◦х6=–х2◦х4◦х7.
(б) план 2IV8-4 имеет определяющее отношение 1=х1◦х2◦х3◦х4 =х1◦х2◦х5◦х8 =х1◦х4◦х6◦х8 =х2◦х4◦х7◦х8.
(в) Пусть план в пункте (б) имеет матрицу B= . Новый план будет иметь матрицу
. Новый план будет иметь матрицу  =
= , которая представляет собой повторённый план 28-4.
, которая представляет собой повторённый план 28-4.
12.5. (а) План 2IV8-4, 1=х1◦х2◦х3◦х4=х1◦х2◦х4◦х6=х1◦х3◦х4◦х7=х2◦х3◦х4◦х8, в двух блоках из восьми опытов каждый.
(б) Пусть b=х1◦х2, так что 1=х1◦х2◦b генерирует разделение на блоки. Тогда можно получить результаты оценки:
1, (A+Bb), B+Ab, C+Eb, D+Fb, E+Cb, F+Db, G+Hb, H+Gb, b+AB+CE+DF+GH, BE+AC+DG+FH, BF+AD+CG+EH, AE+BC+DH+FG, AF+BD+CH+EF, AF+CD+BH+EF, CF+DE+BG+AH.
(в) Воздействия факторов не совмещены, если фактор блоков не взаимодействует.
12.6. Для данного в подсказке плана полное определяющее отношение следующее
1=х1◦х2◦х3◦х5 =х1◦х2◦х4◦х6 =х1◦х2◦b1=х1◦х3◦b2=х3◦х4◦х5◦х6
=х3◦х5◦b1=х2◦х5◦b2=х4◦х6◦b1=х2◦х3◦х4◦х6◦b2
=х2◦х3◦b12=х1◦х2◦х3◦х4◦х5◦х6◦b1=х1◦х4◦х5◦х6◦b2
=х1◦х5◦b12=х1◦х3◦х4◦х6◦b12=х2◦х4◦х5◦х6◦b12.
Из 16 доступных результатов оценки это: среднего, шести воздействий факторов, (b1+AB+CE+EF), (b2+AC+BE), (b12+AE+BC), (AD+BF), (AF+BD), (CD+EF), (взаимодействий высших порядков) и (CF+DE), если факторы блоков не взаимодействуют.
Может быть немного лучше разделить на блоки план посредством b1=х1◦х3◦х4 и b2=х2◦х3◦х4. Это позволит найти результаты оценки среднего, шести воздействий факторов, (b12+AB+CE+DF), (AC+BE), (AE+BC), (AD+BF), (AF+BD), (CD+EF), b1, b2, (CF+DE), если факторы блоков не взаимодействуют. Два воздействия блоков были отделены от наборов двухфакторных взаимодействий. Однако первый план обеспечит два результата оценки воздействий взаимодействий высокого порядка, которые могут быть использованы для оценки s2. Этого второй план не даёт.
12.7. Определяющим отношением (включая разделение на блоки) является
1=х1◦х2◦х3◦х5=х1◦х2◦х4◦х6 =х1◦х2◦b1=х1◦х3◦b2=х1◦х4◦b3.
Полное определяющее отношение:
1=х1◦х2◦х3◦х5=х1◦х2◦х4◦х6 =х1◦х2◦b1=х4◦х6◦b1=х1◦х3◦b2=х1◦х4◦b3=х3◦х4◦х5◦х6=х3◦х5◦b1=х2◦х5◦b2
=х2◦х3◦х4◦х5◦b3=х2◦х3◦х4◦х6◦b2=х2◦х6◦b3=х2◦х3◦b1◦b2=х2◦х4◦b1◦b3=х3◦х4◦b2◦b3=х1◦х5◦b1◦b2
=х1◦х2◦х3◦х4◦х5◦х6◦b1=х1◦х4◦х5◦х6◦b2=х1◦х3◦х5◦х6◦b3 = х1◦х3◦х4◦х5◦b1◦b3=х1◦х2◦х4◦х5◦b2◦b3
=х1◦х3◦х4◦х6◦b1◦b2=х1◦х6◦b1◦b3=х1◦х2◦х3◦х6◦b2◦b3=х1◦х2◦х3◦х4◦b1◦b2◦b3=х2◦х4◦х5◦х6◦b1◦b2
=х2◦х3◦х5◦х6◦b1◦b3=х5◦х6◦b2◦b3=х4◦х5◦b1◦b2◦b3=х3◦х6◦b1◦b2◦b3=х1◦х2◦х5◦х6◦b1◦b2◦b3.
Если факторы блоков не взаимодействуют между собой, а воздействия взаимодействий трех или более факторов игнорируются, то доступны следующие результаты оценки: среднего, A, B, C, D, E, F, (b1+AB+CE+DF), (b2+AC+BE), (b3+AD+BF), (b12+AE+BC), (b13+AF+BD), (b23+CD+EF), (взаимодействия третьего порядка), (b123+CF+DE).
Когда имеется восемь блоков, то в этих условиях не представляется возможным улучшить результаты оценки. Например, если принять b1=х1◦х3◦х4, b2=х2◦х3◦х4, то b1◦b2=х1◦х2. Присвоение b3 любому из остальных столбцов совмещает воздействия факторов с воздействиями блоков. Таким образом, три фактора блоков должны быть отнесены к столбцам, которые обычно оценивают комбинации двухфакторных взаимодействий. (Заметим, что, как и в предыдущем примере, если нужны четыре блока, то можно без проблем принять b1=х1◦х3◦х4 и b2=х2◦х3◦х4.)
12.8. (а) Для начальных восьми опытов определяющее отношение 1=х1◦х2◦х3◦х4=х2◦х3◦х5 =х1◦х4◦х5. Когда к плану применяется метод изменения знаков, то знаки каждого вектора изменяются на противоположные, так что определяющим отношением для второй фракции из восьми опытов является 1=х1◦х2◦х3◦х4=–х2◦х3◦х5 =–х1◦х4◦х5. Объединение этих двух планов (символически, ''усредняя'' два определяющих отношения) дает 1=х1◦х2◦х3◦х4 и, следовательно, планом является 25-1 разрешающей способности IV.
(б) План 2V5-1 с определяющим отношением 1=х1◦х2◦х3◦х4◦х5, как правило, лучше, так как все воздействия факторов и двухфакторных взаимодействий могут быть оценены отдельно.
12.9. Сначала запишите план разрешающей способности III из восьми опытов для шести факторов, например, 1=х1◦х2◦х4=х1◦х3◦х5=х2◦х3◦х6. Добавьте вторую фракцию, в которой только знаки уровней фактора х1 изменены на противоположные, а именно, 1=–х1◦х2◦х4=–х1◦х3◦х5=х2◦х3◦х6. Полные определяющие отношения двух планов, соответственно, следующие:
1=х1◦х2◦х4=х1◦х3◦х5=х2◦х3◦х6=х2◦х3◦х4◦х5=х1◦х3◦х4◦х6=х1◦х2◦х5◦х6=х4◦х5◦х6,
1=–х1◦х2◦х4=–х1◦х3◦х5=х2◦х3◦х6=х2◦х3◦х4◦х5=–х1◦х3◦х4◦х6=–х1◦х2◦х5◦х6=х4◦х5◦х6.
Таким образом, совместный план имеет 1=х2◦х3◦х6=х2◦х3◦х4◦х5=х4◦х5◦х6 и его будут генерировать любые два из трех указанных членов. Воздействие фактора х1 совмещено с воздействиями взаимодействий четырех или пяти факторов и все воздействия взаимодействий двух факторов, включающих х1, совмещены с воздействиями взаимодействий трёх или четырёх факторов, достигая желаемую цель.
12.10. Есть два полных определяющих отношения
1=х1◦х2◦х4=х1◦х3◦х5=х2◦х3◦х6=х2◦х3◦х4◦х5=х1◦х3◦х4◦х6=х1◦х2◦х5◦х6=х4◦х5◦х6,
1=х1◦х2◦х4=–х1◦х3◦х5=–х2◦х3◦х6=–х2◦х3◦х4◦х5=–х1◦х3◦х4◦х6=х1◦х2◦х5◦х6=х4◦х5◦х6.
с общей частью
1=х1◦х2◦х4=х1◦х2◦х5◦х6=х4◦х5◦х6.
Если игнорировать воздействия взаимодействий между тремя или более факторами, то структуры совместных воздействий следующие:
β0 β13
β1= β24 β15= β26
β2= β14 β16= β25
β3 β23
β4= β12= β56 β34
β5= β46 β35
β6= β45 β36
Видно, что воздействия фактора х3 и всех двухфакторных взаимодействий, где он участвует, оцениваемы в индивидуальном порядке. Это происходит потому, что изменение знаков уровней факторов х1 и х2 даёт точно такой же эффект, как изменение знаков уровней фактора х3.
12.11. Сначала возьмём план 24 с факторами х1, х2, х3 и х4. Очевидно, что столбцы x12, x13, x14, x23, x24, x123 уровней взаимодействий факторов не могут быть использованы для новых факторов, так как эти взаимодействия не смогут быть оценены отдельно. Пять столбцов остаются, а именно, х34, х124, х134, х234 и х1234. Если, например, выбрать х5=х34 и х6=х1234, то определяющим отношением будет 1=х3◦х4◦х5=х1◦х2◦х3◦х4◦х6 =х1◦х2◦х5◦х6. Тем не менее, это совмещает х5 с х34 и х15 с х26 и поэтому не годится. Также и другие пары вариантов не работают. Следовательно, такого плана не существует.
(Примечание: Некоторые читатели понимают этот вопрос так, что конкретно не указанные воздействия двухфакторных взаимодействий равны нулю. Если бы это было правдой, то, полагая х5=х34 и х6=х1234, план бы существовал.)
Глава 13
13.1. Нормирование факторов выполняется по формулам х1= (ξ1–90)/10 и х2= (ξ2–20)/10, а нормирование переменных отклика по формуле (13.1.7) даёт вектор  =[–0,062 –1,197 1,796 –0,578 0,041]. Модель для скорейшего улучшения отклика получается в виде
=[–0,062 –1,197 1,796 –0,578 0,041]. Модель для скорейшего улучшения отклика получается в виде
 = –0,8775х1+0,619х2.
= –0,8775х1+0,619х2.
Опыты скорейшего улучшения отклика имеют координаты (х1, х2) =(–0,8775а, 0,619а) для разных значений а или в натуральных единицах измерений (ξ1, ξ2)=(90–8,775а, 20+6,19а).
13.2.  =–0,877х1+0,619х2. Нормированные факторы (х1, х2)=(–0,877а, 0,619а), поэтому в направлении скорейшего улучшения отклика имеем (ξ1, ξ2)=(99–8,77а, 17+12,38а). Нет значения а, дающего (59, 67), поэтому ответ НЕТ.
=–0,877х1+0,619х2. Нормированные факторы (х1, х2)=(–0,877а, 0,619а), поэтому в направлении скорейшего улучшения отклика имеем (ξ1, ξ2)=(99–8,77а, 17+12,38а). Нет значения а, дающего (59, 67), поэтому ответ НЕТ.
13.3. Формулы нормирования факторов х1=(ξ1–90)/10, х2=(ξ1–50)/10 и функция модели  =1,111х1+0,625х2. Нормированные факторы (х1, х2)=(1,111а, 0,625а), поэтому в направлении скорейшего улучшения отклика имеем (ξ1, ξ2)=(90+11,11а, 50+6,25а). Предсказываемые значения переменных отклика находятся по формуле уа=
=1,111х1+0,625х2. Нормированные факторы (х1, х2)=(1,111а, 0,625а), поэтому в направлении скорейшего улучшения отклика имеем (ξ1, ξ2)=(90+11,11а, 50+6,25а). Предсказываемые значения переменных отклика находятся по формуле уа=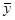 +Sу(1,1112а+0,6252а), где
+Sу(1,1112а+0,6252а), где 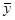 =28,9 и Sу=7,2.
=28,9 и Sу=7,2.
13.4. Для предсказаний используется модель  =хаТ
=хаТ +ε, где
+ε, где  - вектор параметров модели (13.1.20) и предсказание переменной
- вектор параметров модели (13.1.20) и предсказание переменной  делается по формуле
делается по формуле  =хаТb1=аb1Тb1, что является также результатом оценки ожидаемого значения E(
=хаТb1=аb1Тb1, что является также результатом оценки ожидаемого значения E( )=аb1Т
)=аb1Т . Случайные величины
. Случайные величины  и
и  независимы, так как предсказываемая переменная
независимы, так как предсказываемая переменная  считается независимой от п наблюдаемых переменных отклика начального эксперимента, используемых для вычисления
считается независимой от п наблюдаемых переменных отклика начального эксперимента, используемых для вычисления  . Поэтому дисперсия разности
. Поэтому дисперсия разности  –
– получается в виде
получается в виде
D( –
– )=D(
)=D( –аb1Тb1)
–аb1Тb1)
=D(аb1Т +e –аb1Тb1).
+e –аb1Тb1).
Так как аb1Т является постоянной величиной, то имеем
является постоянной величиной, то имеем
D( –
– )=D(e)+D(аb1Тb1)
)=D(e)+D(аb1Тb1)
=s2+s2аb1Т(X1ТX1)–1аb1
=s2[1+а2b1Т(X1ТX1)–1b1],
что можно оценить выражением s2[1+а2b1Т(X1ТX1)–1b1].
Математическое ожидание Е( –
– ) =Е(аb1Т
) =Е(аb1Т +e –аb1Тb1)=0, так как Е(e)=0 и Е(b1)=
+e –аb1Тb1)=0, так как Е(e)=0 и Е(b1)= , а результат s2 оценки дисперсии не зависит от
, а результат s2 оценки дисперсии не зависит от  и
и  =аb1Тb1. Таким образом, здесь статистика tу получается в виде
=аb1Тb1. Таким образом, здесь статистика tу получается в виде
tу=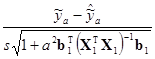
и имеет распределение t(п–р). А то, что с вероятностью 1–α её значения находятся в интервале между –tα/2(п–р) и +tα/2(п–р) можно записать так
Pr[–ta/2(п–р)≤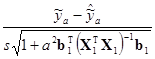 ≤+ta/2(п–р)]=1–a.
≤+ta/2(п–р)]=1–a.
Чтобы получить 100(1–α)% интервал предсказания значений переменной  неравенство в квадратных скобках преобразуется к виду
неравенство в квадратных скобках преобразуется к виду
 –tα/2(п–р)s
–tα/2(п–р)s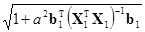 ≤
≤ ≤
≤ +tα/2(п–р)s
+tα/2(п–р)s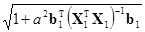
и, учитывая, что  =аb1Тb1, получаем выражение для этого интервала
=аb1Тb1, получаем выражение для этого интервала
Обратите внимание на лекцию "13. Ультразвуковые датчики".
аb1Тb1±s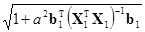 tα/2(п–р).
tα/2(п–р).
Доверительная вероятность 1–a для этого интервала предсказания имеет место только для одного набора значений элементов вектора аb1, так что для результата каждого опыта скорейшего улучшения отклика будет свой интервал предсказания.
Для получения интервала предсказания в натуральных единицах измерений необходимо преобразовать нормированную переменную отклика в натуральные единицы измерений по формуле (13.1.18). И, если в эту формулу вместо  подставить выражение для её интервала предсказания, то в результате получаем формулу расчёта интервала предсказания переменных отклика в опытах скорейшего улучшения отклика в виде
подставить выражение для её интервала предсказания, то в результате получаем формулу расчёта интервала предсказания переменных отклика в опытах скорейшего улучшения отклика в виде
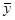 +Sуаb1Тb1±Sуs
+Sуаb1Тb1±Sуs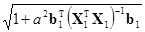 tα/2(п–р).
tα/2(п–р).
При этом, как и при расчёте доверительных интервалов факторов, знак перед вектором аb1 берётся положительным, если отклик увеличивается, а если уменьшается, то знак перед ним берётся отрицательным
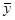 –Sуаb1Тb1±Sуs
–Sуаb1Тb1±Sуs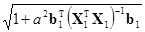 tα/2(п–р).
tα/2(п–р).


 и C(x)=
и C(x)= .
. и C(w)=
и C(w)= .
. .
. имеет распределение N2
имеет распределение N2 .
.
 +
+ ,
, .
. . Заметим, что r13-24 имеет противоположный знак по сравнению с r13.
. Заметим, что r13-24 имеет противоположный знак по сравнению с r13. .
. .
. /4 и r12-3=
/4 и r12-3= .
. =
= . Покажите, что tу=(
. Покажите, что tу=( –y)/(
–y)/( ) имеет распределение N(0, 1).
) имеет распределение N(0, 1).