Распределение по нормальному закону

1.5. Распределение по нормальному закону

Результаты повторных опытов изменяются из-за вариации и часто варьируют около некоторого центрального значения в приблизительно симметричном распределении, где малые отклонения происходят много чаще, чем большие. Для представления этой ситуации ценным в статистике теоретическим распределением является распределение по нормальному закону. Оно изображается симметричной кривой с наивысшей ординатой в её центре и спускающейся к нулю в обоих направлениях в виде интуитивно ожидаемой вариации результатов повторяемого опыта эксперимента. Это показанный на Рис.1.5.1 график функции плотности вероятности

f(у)=exp,

являющейся функцией от нормированной разности (у–y)/s в квадрате.

Важность распределения по нормальному закону объясняется двумя доводами:

1. Эффектом центрального предела, обеспечивающим стремление реальных распределений ошибок быть распределёнными приблизительно по нормальному закону.

2. Толерантностью некоторых общих статистических методов к отклонениям от теоретического распределения по нормальному закону.

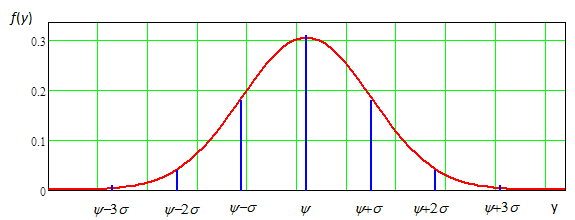
Рис.1.5.1. График функции плотности вероятности распределения по нормальному закону.

Рекомендуемые материалы

Эффект центрального предела

Обычно, случайная ошибка находится по формуле e=y–y, где y - результат отдельного опыта и y - ожидаемое значение популяции результатов этого опыта. Она является результатом сложения некоторого числа составляющих ошибок. Так, значение результата отдельного опыта эксперимента может быть подвержено ошибке измерения e₁, ошибке e₂ выборки, ошибке e₃ получаемой из-за невозможности точно удовлетворить требуемые условия проведения опыта, ошибке e₄ из-за использования различных исходных материалов и других ошибок. Таким образом, общая ошибка e является функцией некоторого числа составляющих e₁, e₂, ..., e_n. Если каждая отдельная составляющая достаточно мала, то обычно возможно аппроксимировать общую ошибку линейной комбинацией её составляющих

e =а₁e₁+а₂e₂+...+а_ne_n,                                               (1.5.1)

где а₁, а₂, ..., а_n – постоянные числа. Теорема о центральном пределе гласит, что при условиях, которым почти всегда удовлетворяют проводимые в реальности опыты экспериментов, и увеличении числа n составляющих ошибок распределение такой линейной комбинации будет стремиться к нормальному. Стремление к распределению по нормальному закону происходит независимо от распределений отдельных составляющих. Однако важным условием является то, чтобы несколько источников ошибок вносили существенные вклады в общую ошибку и ни один из источников не доминировал над остальными.

Стремление усреднённых к центральному пределу

Рассмотрим распределения, получаемые при кидании правильных шестигранных игральных костей [Box с соавт. (2005) стр.30]. При кидании одной такой кости вероятности выпадения 1, 2, 3, 4, 5 или 6 очков все равны 1/6. Среднее подсчета очков по всем граням кости равно h =3,5. Чтобы увидеть как эффект центрального предела проявляется при усреднениях, положим, что e₁, e₂, ..., e_n обозначают разности получаемых очков бросаемых костей и среднего h =3,5. Пусть е - соответствующее усреднённое разностей от среднего h для п бросаемых костей, то есть е=. Тогда е определяется выражением (1.5.1), где все коэффициенты а равны 1/n. Несмотря на то, что исходное распределение индивидуальных наблюдений (подсчёты очков при единичных бросаниях) имеют далеко ненормальную форму, ординаты распределения усреднённых подсчета очков являются поразительно сходными ординатам распределения по нормальному закону даже для такого малого n как 2.

С использованием программы Mathcad 13 это можно показать так. Если усреднённые значения подсчётов очков бросаемых костей распределены по нормальному закону, то можно воспользоваться встроенной в Mathcad 13 функцией rnorm(k,h,s), где k=1000 - число генерируемых этой функцией случайных усреднённых подсчетов очков. Тогда, если принять s=0,8, то при h=3,5 нижний и верхний пределы значений усреднённых рассматриваемого распределения равны приблизительно 1 и 6. Поэтому получаемая на основе этих данных гистограмма распределения усреднённых подсчётов очков при бросании двух игральных костей 1000 раз принимает вид, как показано на Рис.1.5.2.

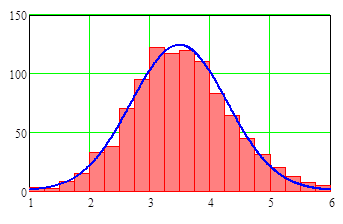
Рис.1.5.2. Распределение усреднённых подсчётов очков для 1000 бросаний двух игральных костей.

В итоге:

1. Как обычно, когда ошибка опыта эксперимента представляет собой совокупность некоторого числа составляющих ошибок, то её распределение стремится к нормальному, даже если распределения составляющих ошибок явно отличны от нормального.

2. Усреднённое выборки наблюдений стремится быть распределённым по нормальному закону, даже если индивидуальные наблюдения, по которым оно вычислено, распределены не по нормальному закону. Следовательно, статистические методы, зависящие не прямо от распределений индивидуальных наблюдений, а от распределений их усреднений, становятся независимы от отличных от нормальных распределений индивидуальных наблюдений.

3. Методы сравнения средних обычно нечувствительны к распределениям отличным от нормального. Однако это не всегда верно при сравнении дисперсий.

Толерантность к отклонению от нормального распределения

Важно помнить, что все статистические модели являются приближёнными. В частности, никогда не было и не будет таких результатов наблюдений, которые в точности следуют распределению по нормальному закону. Поэтому, несмотря на то, что многие описанные здесь процедуры и модели выводятся при допущении распределения по нормальному закону, обычно, приблизительная нормальность будет тем, что требуется для них, чтобы быть полезными. В частности, методы сравнения средних значений обычно толерантны к отклонениям от нормального распределения. Если нет специального предостережения, то нет необходимости сильно беспокоиться о нормальности. Однако необходимо быть всегда настороже и проверять грубые нарушения этого и всех других допущений.

Описание распределения по нормальному закону

Когда даны среднее y и дисперсия s² нормального распределения случайной переменной (у), то всё её распределение описано. Часто используется форма записи N(y, s²) чтобы показать, что рассматривается распределение по нормальному закону, имеющее среднее y и дисперсию s². Так, запись N(30, 25) определяет нормальное распределение со средним y =30 и дисперсией s²=25. Графики функций плотности вероятности распределений N(–5, 25), N(5, 100), N(30, 25) и N(30, 6,25) показаны на Рис.1.5.3.

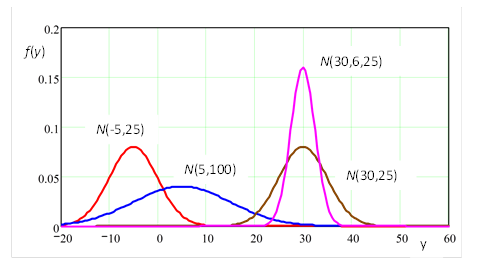
Рис.1.5.3. Графики функций плотности вероятности распределений по нормальному закону с различными средними и дисперсиями.

Для нормального распределения стандартное отклонение s представляет собой расстояние между средним y и точкой перегиба кривой распределения. На Рис.1.5.4 показано, что точка перегиба является пунктом, в котором наклон кривой прекращает расти, и начинает уменьшаться (или наоборот). Перечисленные ниже сведения приведены с целью получения более полного понимания нормального распределения:

1. Вероятность того, что положительное отклонение от среднего y превзойдёт одно стандартное отклонение, равна 0,1587 (≈1/6). Эта вероятность представлена на Рис.1.5.4 заштрихованной площадью «хвостовой» области под кривой.

2. Из-за симметрии функции распределения, эта вероятность в точности равна вероятности, что отрицательное отклонение от среднего y будет меньше одного отрицательного стандартного отклонения.

3. Из предыдущих двух утверждений получается, что вероятность отклонения в обоих направлениях за пределы одного стандартного отклонения составляет 2х0,1587=0,3174 (≈1/3).

4. Следовательно, вероятность того, что отклонения от среднего y в обоих направлениях не выйдут за пределы стандартного отклонения, равна 0,6826 (≈2/3).

5. Вероятность того, что положительное отклонение от среднего y будет меньше одного стандартного отклонения, равна 0,8413 (≈5/6).

6. Вероятность, что положительное отклонение от среднего превзойдёт два стандартных отклонения, равна 0,0228 (≈1/40). Эта вероятность представлена на Рис.1.5.4 удвоено заштрихованной областью.

7. Снова, эта вероятность в точности равна вероятности того, что отрицательное отклонение от среднего выйдет за предел двух стандартных отклонений.

8. Из предыдущих двух утверждений вероятность, что отклонения в обоих направлениях выйдут за пределы двух стандартных отклонений, равна 0,0456 (≈1/20 или 0,05). Следовательно, вероятность того, что отклонения от среднего y в обоих направлениях не выйдут за пределы двух стандартных отклонений, равна 0,9544 (≈19/20 или 0,95).

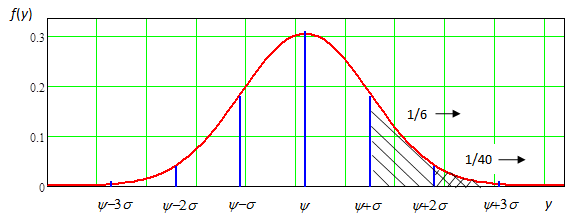
Рис.1.5.4. Площади хвостовых частей под кривой функции плотности вероятности распределения по нормальному закону.

Вероятностное утверждение относительно некоторой нормально распределённой случайной переменной (у) часто наилучшим образом выражается через нормированную случайную переменную z=(у–y)/s. Эта случайная переменная z имеет распределение N(0, 1), то есть распределена по стандартному нормальному закону со средним равным 0 и дисперсией равной 1. С использованием этой переменной приведённые выше утверждения можно переписать следующим образом:

1. Pr(y>y +s) =Pr[(y–y)>s] =Pr[(y–y)/s>1] =Pr(z>1) =0,1587
2. Pr(z<–1) =0,1587
3. Pr(|z|>1) =0,3174
4. Pr(|z|<1) =0,6826
5. Pr(z<1) =0,8413
6. Pr(z>2) =0,0228
7. Pr(z<–2) =0,0228
8. Pr(|z|>2) =0,0456.

Расчёт вероятностей нормального распределения

Для нахождения вероятности Pr(у>y₀), то есть, что значение случайной переменной (у) превзойдёт некоторое значение y₀, можно вычислить значение нормированной случайной переменной z₀=(y₀–y)/s и найти вероятность Pr(z>z₀) по таблице, приведённой в книге [Box с соавт. (2005) стр. 612]. (Вероятности для нормированной случайной переменной вычисляются на многих ручных калькуляторах.) Например, дана популяция наблюдений, распределённых по нормальному закону со средним y =39 и дисперсией s²=16. Какова вероятность получения результата наблюдения большего 42, то есть Pr(у>42)? При известном среднем значении и дисперсии значение нормированной случайной переменной получается z₀=(42–39)/4=0,75 и искомая вероятность Pr(z>0,75)=0,227.

В общем, вероятность Pr(у>y₀) вычисляется с использованием функции интегральной вероятности нормального распределения в зависимости от среднего и стандартного отклонения. Эта функция имеет вид

Pr_н= или Pr_н=pnorm(y₀, y, s),                        (1.5.2)

где pnorm(y₀, y, s) – встроенная функция компьютерной программы Mathcad 13. По этой функции вычисляется затенённая площадь под кривой на Рис.1.5.5, а незатенённая площадь под кривой равна вероятности Pr(у>y₀), которая находится из выражения

Pr(у>y₀)=1–Pr_н=1–pnorm(y₀, y, s).                                    (1.5.3)

И для рассматриваемого примера имеем Pr(у>42)=1–pnorm(42, 39, 4)=0,227.

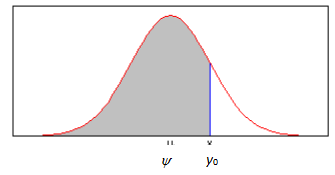
Рис.1.5.5. Графическое представление интегральной вероятности нормального распределения.

Люди также интересуются этой лекцией: 4 Решение транспортной задачи с помощью ЭВМ.

В качестве второго примера дано распределение N(39, 16). Какова вероятность, что результаты наблюдений будут находиться в интервале (33<у<45)? Для представления этой и ей подобных проблем полезно сделать эскиз нормального распределения со средним 39 и стандартным отклонением 4 и заштриховать площадь под вопросом, как показано на Рис.1.5.6. Из рисунка видно, что искомая вероятность

Pr_н(33<у<45)=pnorm(45, 39, 4)–pnorm(33, 39, 4)=0,866.

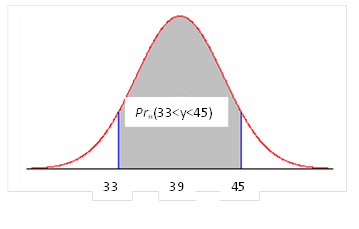
Рис.1.5.6. Графическое представление искомой интегральной вероятности нормального распределения.

Упражнение 1.5.1. Процент метанола в партиях изделия имеет по спецификации верхний предел 0,15%. Записанные данные подсказывают, что наблюдения метанола могут быть описаны нормальным распределением со средним равным 0,10% и стандартным отклонением равным 0,02%. Какова вероятность выхода за пределы спецификации?

Упражнение 1.5.2. По спецификации нижний и верхний пределы конденсаторов в цепи равны соответственно 2,00мкФ и 2,08мкФ. Ёмкости производимых конденсаторов распределены примерно по нормальному закону со средним 2,50мкФ и стандартным отклонением 0,02мкФ. Какая часть производимых изделий будет находиться в пределах спецификации?