Связь между гладкостью функции и периодом малости коэффициентов Фурье

Лекция 2.

Связь между гладкостью функции и периодом малости коэффициентов Фурье.

Теорема. Пусть функция  определена на отрезке ,   разлагается на нем в тригонометрический ряд Фурье и непрерывна на нем вместе со своими производными до p –1 порядка включительно. Пусть  Если p –ая производная функции  кусочно непрерывна на интервале , то коэффициенты Фурье - бесконечно малые функции по отношению к .

Доказательство.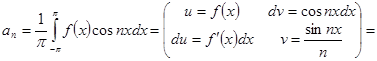

.

 Здесь - коэффициенты Фурье для функции .

Продолжая аналогично интегрирование по частям, получим

Рекомендуемые материалы

. Из этих соотношений следует

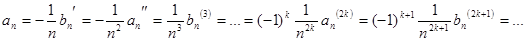
Из этого соотношения или непосредственно можно получить аналогичное соотношение для .

Поэтому , где  или  - n –ый коэффициент Фурье.

По следствию из равенства Парсеваля   для коэффициентов Фурье самой функции и ее производных.. Следовательно, _0. Теорема доказана.

Пример. Разложить в ряд Фурье функцию  и построить график суммы ряда .

Продолжим заданную функцию периодически на всю ось. Тогда функция будет иметь разрывы первого рода в точках . В этих точках функция  будет принимать значение , равное, по теореме Дирихле, полу сумме левого и правого пределов функции . В остальных точках значения функций   и  будут совпадать.

Вычислим коэффициенты Фурье.

,

.

. Проверьте, выполнив интегрирование по частям.

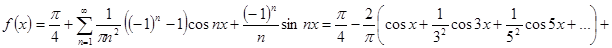
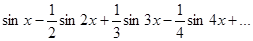
Из таких разложений часто можно получать суммы числовых рядов.

Например, подставим в разложение , получим

.

Подставим в разложение , получим

.

Разложения в ряд Фурье функций, заданных на отрезке .

Выше были получены формулы коэффициентов ряда Фурье при разложении в ряд функции, заданной на отрезке  (или периодических функций с периодом ).

Выведем формулы коэффициентов ряда Фурье при разложении в ряд функции, заданной на отрезке .

Если функция  задана на отрезке  (или периодическая с периодом ), то функция  имеет период  (первое свойство периодических функций). Поэтому ее можно разложить в ряд Фурье для функции с периодом .

= .

,  ,  .

Сделаем в этих формулах замену переменных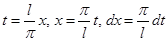

,  , .

=   (в точках непрерывности функции).

В точках разрыва функции . Возвращаясь к переменной x, заменяя формально t на x, получим формулы коэффициентов ряда Фурье при разложении в ряд функции, заданной на отрезке .

,  , .

 =  (в точках непрерывности функции).

В точках разрыва функции .

Пример. Разложить в ряд Фурье функцию , не вычисляя коэффициенты ряда Фурье.

Функция непрерывна, по теореме Дирихле

,

,

,

,

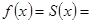
Разложение в ряд Фурье четных и нечетных функций.

Свойства четных и нечетных функций.

1) произведение четных функций – четная функция. Произведение нечетных функций – четная функция, произведение четной функции на нечетную – нечетная функция.

Обозначим  - нечетную и четную функции. ,

Получим, ,

.

2)

.

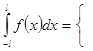
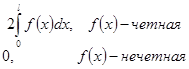
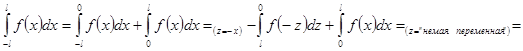
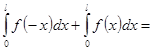
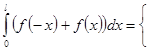
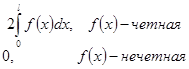Рассмотрим формулы разложения функции , заданной на отрезке  в ряд Фурье

,  , .

 =  (в точках непрерывности функции).

В точках разрыва функции .

Если функция  четна, то по четности косинуса, нечетности синуса и свойству 1 под интегральные функции в . Следовательно,

,  , .

 =  (в точках непрерывности функции). Четная функция разлагается по четным функциям.

Если функция  нечетна, то по четности косинуса, нечетности синуса и свойству 1 под интегральные функции в . Следовательно,

,  ,..

 =   (в точках непрерывности функции). Нечетная функция разлагается по нечетным функциям.

Разложение в ряд Фурье функций, заданных на отрезке  по синусам и косинусам кратных дуг.

Так как функция задана на отрезке , то ее можно доопределить на отрезок  четным или нечетным образом.

Если функция доопределена четным образом, то она, как четная функция может быть разложена по формулам для четной функции

,  , .

 =  (в точках непрерывности функции).

Это – разложение в ряд Фурье по косинусам кратных дуг.

Если функция доопределена нечетным образом, то она, как нечетная функция может быть разложена по формулам для нечетной функции

,  ,..

 =   (в точках непрерывности функции).

Это – разложение в ряд Фурье по синусам кратных дуг.

Одну и ту же функцию, заданную на отрезке , можно разложить и по синусам, и по косинусам кратных дуг.

 Пример. Разложить по косинусам и синусам кратных дуг функцию , заданную на отрезке   .

Так как мы доопределяем функцию на отрезок  при разложении по косинусам и синусам кратных дуг, то .

Разложим функцию по косинусам кратных дуг.

Вам также может быть полезна лекция "44. Плазматическая мембрана".

,  , .

 ==1.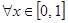

Разложим функцию по синусам кратных дуг.

,  ,..

 = =  ,

 (теорема Дирихле).