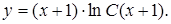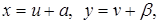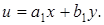Дифференциальные уравнения, приводящиеся к однородным

Дифференциальные уравнения, приводящиеся к однородным

     Дифференциальное уравнение вида

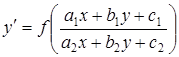
называется приводящимся к  однородному.  В  частности,  к  этому классу относится уравнение вида

                                   (1.10)

     Некоторые из коэффициентов (но не одновременно  и ) могут быть равны нулю.

     Следует различать два случая:

Рекомендуемые материалы

    1) Если определитель, то уравнение(1.10)

приводится к однородному подстановкой 

                 (1.11)
                   

где постоянные  и  определяются из системы уравнений:

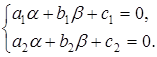
     Действительно, учитывая, что   следо-

вательно,  , и подставляя (1.11) в (1.10), полу-

чим    - однородное уравнение относительно

новой функции v(u). Полагая далее  t=v/u, приводим последнее уравнение к уравнению с разделяющимися переменными.

   2)Если определитель , то уравнение (1.10)

сразу приводится к уравнению с разделенными переменными  заменой

    Пример. Решить уравнение   

В этом уравнении       Поэтому

. Полагая    находим  и  из

системы уравнений:                                   

   следовательно,     

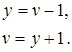
     Уравнение приводится к однородному

Информация в лекции "Правый желудочек" поможет Вам.

Полагая далее   приходим к уравнению с разделяющимися переменными относительно функции t:

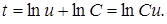
     Возвращаясь к старой переменной, получим