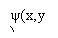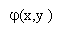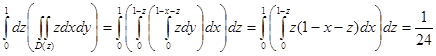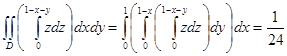Тройной интеграл
Лекция 3 Тройной интеграл.
Задача о массе пространственного тела.
Пусть есть некоторое пространственное материальное тело, занимающее область V, в каждой точке которой задана объемная плотность f(x, y, z). Надо вычислить массу пространственного тела.
Эта задача приводит к понятию тройного интеграла.
Введем разбиение области V на элементарные области, не имеющие общих внутренних точек (условие А) Dvk с малым объемом 
(обозначение области и ее объема обычно одно и то же, это принято уже более 200 лет и не вносит путаницы).
На каждом элементе разбиения – элементарной области отметим точку Mk(xk, yk, zk). Вычислим плотность в этой точке f(xk, yk, zk) = f(Mk) и предположим, что плотность постоянна в элементарной области. Тогда масса элементарной области Dvk приближенно равна = f(Mk) . Суммируя все такие массы элементарных областей (составляя
интегральную сумму), приближенно получим массу области V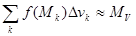 
Для того, чтобы точно вычислить массу области, остается перейти к пределу при условии 
(условие B).
Рекомендуемые материалы
.
Так задача о массе пространственной области приводит к тройному интегралу[1].
Введем некоторые ограничения на область интегрирования и подинтегральную функцию, достаточные для существования интеграла[2].
Потребуем, чтобы функция f(M) была непрерывна в области V и на ее границе.
Потребуем, чтобы область V была замкнутой, ограниченной, пространственно-односвязной областью с кусочно-гладкой границей.
Область назовем пространственно-односвязной, если ее можно непрерывной деформацией стянуть в точку.
Теорема существования. Пусть область V и функция f(M)=f(x, y, z) удовлетворяют сформулированным требованиям. Тогда тройной интеграл существует как предел интегральных сумм.
.
Замечание. Предел этот не зависит[3]:
1) от выбора разбиения области, лишь бы выполнялось условие А
2) от выбора отмеченных точек на элементах разбиения
3) от способа измельчения разбиения, лишь бы выполнялось условие B.
Свойства тройного интеграла.
1. Линейность
а) 
=
+
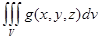
б) 
=
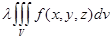
Эти свойства, как и для двойного интеграла, доказываются «через интегральные суммы». Составляют интегральную сумму для интегралов, стоящих в левой части равенства, в ней делают нужную операцию (это возможно, т.к. число слагаемых конечно) и получают интегральные суммы для интегралов в правой части. Затем, по теореме о предельном переходе в равенстве, переходят к пределу, и свойство доказано.
2. Аддитивность (по множеству)
=+
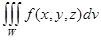
Доказательство проводится, как и ранее, через интегральные суммы с использованием замечания к теореме существования.
Разбиение выбирается и измельчается так, чтобы граница областей V, W состояла из границ элементов разбиения (это можно сделать, учитывая замечание). Тогда интегральная сумма для интеграла в левой части равенства равна сумме двух интегральных сумм, каждая для своего для интеграла в правой части равенства. Переходя к пределу в равенстве, получаем требуемое соотношение.
3. 
, где 
– объем области V.
Интегральная сумма для интеграла в левой части 
= 
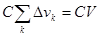
4. Если f(x, y, z) ³g(x, y, z), то ³.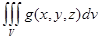
Переходя к пределу в неравенстве 
³
(по теореме о переходе к пределу в неравенстве), получим требуемое соотношение.
Следствие. Если f(x, y, z) ³0, то ³0.
5. Теорема об оценке интеграла. Если m £f(x, y, z) £M, то mV££MV.
Интегрируя неравенство m £f(x, y, z) £M, по свойству 4 получим требуемое неравенство.
6. Теорема о среднем. Пусть выполнены требования теоремы существования. Тогда
Существует точка С в области V, такая, что f(C) =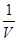 
.
Доказательство. Так как функция 
непрерывна на замкнутом ограниченном множестве , то существует ее нижняя грань 
и верхняя грань 
. Выполнено неравенство 
. Деля обе части на получим 
. Но число 
заключено между нижней и верхней гранью функции. Так как функция непрерывна на замкнутом ограниченном множестве , то в некоторой точке 
функция должна принимать это значение. Следовательно, 
.
Вычисление тройного интеграла в декартовой системе координат.
|
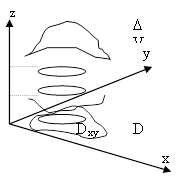
| Пусть пространственное тело проектируется на плоскость OXY в область D, а на ось OZ в отрезок [c, d].Пусть «верхняя» граница тела описывается уравнением поверхности z = y(x, y), «нижняя» – уравнением z = j(x, y). Пусть элемент DV пространственного тела V проектируется на плоскость OXY в область Dxy , а на ось OZ в отрезок [z, z+Dz]. Для того чтобы вычислять тройной интеграл как предел интегральных сумм, нужно в интегральной сумме перебирать эти элементы по определенному алгоритму. |
Если сначала перебирать элементы в столбце над областью Dxy, от нижней границы до верхней (внутренний интеграл), а затем перемещать область Dxy в D (внешний двойной интеграл), то получим повторный интеграл
.
Если сначала перебирать элементы в слое [z, z+Dz] (внутренний интеграл), а затем .перемещать слой на [c, d], (внешний интеграл), то получим повторный интеграл 
.И в том, и в другом случае тройной интеграл сводится к определенному и двойному интегралам.
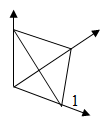
Пример. Вычислить массу тетраэдра плотностью f(x, y, z) = z, ограниченного плоскостями x+y+z = 1, x+z =1, x+y = 1, y+z =1.
| Лекция "5.3 Усиление абсолютизма в первой половине XIX в" также может быть Вам полезна.
|
|
[1] Здесь интеграл вводится несколько упрощенно. Более строгое определение интеграла приведено в выпуске VII учебника.
[2] Эти требования можно ослабить, распространив интеграл на функции со счетным числом разрывов первого рода (выпуск VII.учебника).
[3] Это очевидно, иначе предел не существует, но это стоит подчеркнуть.
