Поверхностные интегралы
16.4. Поверхностные интегралы.
16.4.1. Односторонние и двусторонние поверхности. Ориентация поверхности. Поверхность может быть односторонней и двусторонней. Простой пример модели односторонней поверхности - лист Мёбиуса, который получается, если взять узкую длинную полоску бумаги и склеить её узкие торцы, перекрутив полоску один раз. В том, что у полученной поверхности одна сторона, можно убедиться, если начать закрашивать её в какой-нибудь цвет, не отрывая кисть от бумаги и не пересекая границ. В результате будет окрашен весь лист Мёбиуса. Мы будем рассматривать только двусторонние поверхности.
Поверхность называется гладкой, если в каждой её точке существует касательная плоскость, непрерывно меняющаяся вдоль поверхности. Поверхность называется кусочно-гладкой, если она состоит из нескольких гладких частей, примыкающим друг к другу по гладким или кусочно- гладким кривым. Так, плоскость - гладкая поверхность; поверхность куба - кусочно-гладка.
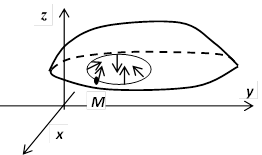
Дадим формальное определение односторонней и двусторонней поверхностей. Пусть дана гладкая поверхность  , и на ней произвольно выбрана точка М. Из двух возможных направлений нормали в этой точке выберем одно и зафиксируем его. Характеризовать это направление будем единичным вектором нормали
, и на ней произвольно выбрана точка М. Из двух возможных направлений нормали в этой точке выберем одно и зафиксируем его. Характеризовать это направление будем единичным вектором нормали  . Возьмём замкнутый контур С, проходящий через точку М, целиком лежащий в
. Возьмём замкнутый контур С, проходящий через точку М, целиком лежащий в  и не пересекающий её границы, и будем двигаться по контуру, восстанавливая в каждой точке нормаль так, чтобы она непрерывно получалось из
и не пересекающий её границы, и будем двигаться по контуру, восстанавливая в каждой точке нормаль так, чтобы она непрерывно получалось из  . Если для любого такого контура и любой точки М мы вернёмся в М с исходным направлением нормали, то поверхность
. Если для любого такого контура и любой точки М мы вернёмся в М с исходным направлением нормали, то поверхность  называется двусторонней. Если хотя бы для одного контура мы вернёмся в исходную точку с противоположным направлением нормали, то поверхность называется односторонней.
называется двусторонней. Если хотя бы для одного контура мы вернёмся в исходную точку с противоположным направлением нормали, то поверхность называется односторонней.
Задать ориентацию поверхности (выбрать определённую сторону поверхности) означает выбрать в каждой точке  один из двух возможных векторов нормали
один из двух возможных векторов нормали  так, чтобы он непрерывно менялся от точки к точке. Для этого достаточно определить нормаль
так, чтобы он непрерывно менялся от точки к точке. Для этого достаточно определить нормаль  в какой-либо одной точке
в какой-либо одной точке  ; во всех остальных точках М направления нормали
; во всех остальных точках М направления нормали  должны браться так, чтобы они получались непрерывным переносом из
должны браться так, чтобы они получались непрерывным переносом из  вдоль какого-нибудь пути
вдоль какого-нибудь пути  . Согласно определению двусторонней поверхности, мы гарантированно придём в точку
. Согласно определению двусторонней поверхности, мы гарантированно придём в точку  с одним и тем же направлением нормали при любом пути
с одним и тем же направлением нормали при любом пути  .
.
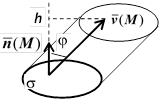
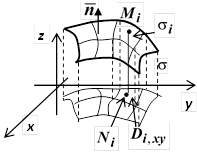
16.4.2. Поток жидкости через поверхность. Как и при изучении криволинейных интегралов, начнём с физической задачи. Пусть через объём V течёт поток жидкости, имеющий скорость  в точке М. Пусть в V размещена проницаемая (возможно, воображаемая) поверхность
в точке М. Пусть в V размещена проницаемая (возможно, воображаемая) поверхность  . Требуется найти количество
. Требуется найти количество  жидкости, протекающей через
жидкости, протекающей через  за единицу времени. В дальнейшем мы будем называть это количество потоком через поверхность.
за единицу времени. В дальнейшем мы будем называть это количество потоком через поверхность.
В случае, когда  - ограниченная плоская область и
- ограниченная плоская область и  , решение очевидно. Это количество равно объёму, ограниченному цилиндрической поверхностью с основанием
, решение очевидно. Это количество равно объёму, ограниченному цилиндрической поверхностью с основанием  и боковой стороной
и боковой стороной  . Площадь основания объёма равна
. Площадь основания объёма равна  (этим символом мы обозначаем и поверхность, и её площадь), высота
(этим символом мы обозначаем и поверхность, и её площадь), высота  , т.е. равна скалярному произведению вектора скорости на единичный вектор нормали. Итак,
, т.е. равна скалярному произведению вектора скорости на единичный вектор нормали. Итак,  . Заметим, что изобразив на рисунке единичный вектор нормали, мы ввели на поверхности ориентацию. Так, применительно к рисунку справа, мы выбрали верхнюю сторону поверхности; если бы выбрали противоположную нормаль, поток изменил бы знак.
. Заметим, что изобразив на рисунке единичный вектор нормали, мы ввели на поверхности ориентацию. Так, применительно к рисунку справа, мы выбрали верхнюю сторону поверхности; если бы выбрали противоположную нормаль, поток изменил бы знак.
Рекомендуемые материалы
Возможны два способа представления этой величины.
1. Обозначив  , получим
, получим  .
.
2. Если в некоторой координатной системе  имеет координаты P, Q, R, единичный вектор
имеет координаты P, Q, R, единичный вектор  имеет координаты - направляющие косинусы
имеет координаты - направляющие косинусы  , то
, то  . Чему равно произведение
. Чему равно произведение  ?
?
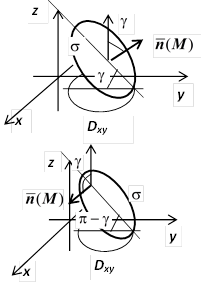
Произведение  равно площади
равно площади  проекции
проекции  поверхности
поверхности  на плоскость Oxy (площади всегда положительны). Следовательно,
на плоскость Oxy (площади всегда положительны). Следовательно,  равно
равно  , если
, если  (или, что то же самое, угол
(или, что то же самое, угол  - острый; проекция
- острый; проекция  на орт
на орт  оси Oz положительна). Этот случай соответствует верхнему рисунка справа. Соответственно,
оси Oz положительна). Этот случай соответствует верхнему рисунка справа. Соответственно,  равно
равно  , если
, если  (или, что то же самое, угол
(или, что то же самое, угол  - тупой; проекция
- тупой; проекция  на орт
на орт  оси Oz отрицательна). Этот случай соответствует нижнему рисунку. Итак, можно записать
оси Oz отрицательна). Этот случай соответствует нижнему рисунку. Итак, можно записать  . Аналогично изложенному,
. Аналогично изложенному,  , где следует взять знак "+", если угол
, где следует взять знак "+", если угол  - острый, и "-", если этот угол тупой, и
- острый, и "-", если этот угол тупой, и  , где берётся знак "+", если угол
, где берётся знак "+", если угол  - острый, и "-", если этот угол тупой;
- острый, и "-", если этот угол тупой;  - проекция
- проекция  на плоскость Oyz,
на плоскость Oyz,  - - проекция
- - проекция  на плоскость Oxz. Окончательно,
на плоскость Oxz. Окончательно,  .
.
Пусть теперь  - произвольная гладкая ограниченная поверхность, и скорость
- произвольная гладкая ограниченная поверхность, и скорость  может меняться от точки к точке. Чтобы свести этот случай к предыдущему, разобьём
может меняться от точки к точке. Чтобы свести этот случай к предыдущему, разобьём  сетью кривых на
сетью кривых на  частей
частей  , на каждой из частей
, на каждой из частей  выберем произвольную точку
выберем произвольную точку  , и, считая, что
, и, считая, что  - плоская область, скорость
- плоская область, скорость  по
по  постоянна и равна
постоянна и равна  и что ориентация всей части
и что ориентация всей части  характеризуется единичным нормальным вектором
характеризуется единичным нормальным вектором  , получим, что через
, получим, что через  в единицу времени протекает
в единицу времени протекает  жидкости (
жидкости ( ). Как мы видели, это выражение можно представить и в виде
). Как мы видели, это выражение можно представить и в виде  (где
(где 
 - угол между
- угол между  и
и  ), и в виде
), и в виде  . Суммируя эти выражения по всем
. Суммируя эти выражения по всем  дугам, получим выражения двух интегральных сумм:
дугам, получим выражения двух интегральных сумм:  и
и  . Переход к пределу в этих интегральных суммах при
. Переход к пределу в этих интегральных суммах при  приведёт к двум поверхностным интегралам:
приведёт к двум поверхностным интегралам:  и
и  . Первый из этих интегралов называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности. Во втором интеграле элементы площади в координатных плоскостям принято записывать так, как мы это делали в двойном интеграле:
. Первый из этих интегралов называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности. Во втором интеграле элементы площади в координатных плоскостям принято записывать так, как мы это делали в двойном интеграле:  и опускать знаки перед слагаемыми:
и опускать знаки перед слагаемыми:  ; этот интеграл называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам. Как и криволинейные интегралы двух родов, это разные объекты. Они имеют разные определения и разные свойства. В частности, поверхностный интеграл первого рода не зависит от ориентации поверхности, так как угол
; этот интеграл называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам. Как и криволинейные интегралы двух родов, это разные объекты. Они имеют разные определения и разные свойства. В частности, поверхностный интеграл первого рода не зависит от ориентации поверхности, так как угол  входит в подынтегральную функцию в явном виде, в то время как поверхностный интеграл второго рода меняет знак при изменении стороны поверхности (вектор
входит в подынтегральную функцию в явном виде, в то время как поверхностный интеграл второго рода меняет знак при изменении стороны поверхности (вектор  меняется на
меняется на  ).
).
Перейдём к формальным определениям.
16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
16.4.3.1. Определение поверхностного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая поверхность  , на которой определена функция f(x,y,z). Разобьём поверхность на
, на которой определена функция f(x,y,z). Разобьём поверхность на  частей
частей  , на каждой из частей
, на каждой из частей  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  и площадь части
и площадь части  (которую будем обозначать тем же символом
(которую будем обозначать тем же символом  ), и составим интегральную сумму
), и составим интегральную сумму  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности  на части
на части  , ни от выбора точек
, ни от выбора точек  , то функция f(x,y,z) называется интегрируемой по поверхности
, то функция f(x,y,z) называется интегрируемой по поверхности  , а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности, и обозначается
, а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности, и обозначается  .
.
Теорема существования. Если функция f(x,y,z) непрерывна на поверхности  , то она интегрируема по этой поверхности.
, то она интегрируема по этой поверхности.
16.4.3.2. Свойства поверхностного интеграла первого рода. Для этого интеграла имеют место основные шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Седьмое, персональное, свойство - независимость поверхностного интеграла первого рода от выбора стороны поверхности.
16.4.3.3. Вычисление поверхностного интеграла первого рода.
16.4.3.3.1. Определение единичного вектора нормали к поверхности. Выражения для элемента площади поверхности. Предположим, что поверхность  задаётся неявным уравнением
задаётся неявным уравнением  (
( - непрерывно дифференцируемая функция) и взаимно однозначно проецируется в область
- непрерывно дифференцируемая функция) и взаимно однозначно проецируется в область  на плоскости Оху. Из теории функций нескольких переменных известно, что градиент функции ортогонален поверхности уровня этой функции, проходящей через точку, в которой найден градиент. Рассматривая уравнение
на плоскости Оху. Из теории функций нескольких переменных известно, что градиент функции ортогонален поверхности уровня этой функции, проходящей через точку, в которой найден градиент. Рассматривая уравнение  как уравнение поверхности уровня функции трёх переменных
как уравнение поверхности уровня функции трёх переменных  , получаем, что в каждой точке поверхности
, получаем, что в каждой точке поверхности 
 ортогонален
ортогонален  , т.е. является нормальным к
, т.е. является нормальным к  вектором. Чтобы получить единичный нормальный вектор, достаточно просто пронормировать
вектором. Чтобы получить единичный нормальный вектор, достаточно просто пронормировать  :
:  , где знак перед дробью соответствует возможности выбора двух возможных взаимно противоположных направлений нормали. В координатной форме
, где знак перед дробью соответствует возможности выбора двух возможных взаимно противоположных направлений нормали. В координатной форме  , где
, где  - базисные орты. Если сравнить это выражение с представлением градиента через направляющие косинусы:
- базисные орты. Если сравнить это выражение с представлением градиента через направляющие косинусы:  , то
, то  ,
,  ,
,  . Теперь мы можем выразить элемент площади поверхности через элемент площади в каждой координатной плоскости:
. Теперь мы можем выразить элемент площади поверхности через элемент площади в каждой координатной плоскости:  ,
,  ,
,  . В частном случае задания уравнения поверхности в явном виде
. В частном случае задания уравнения поверхности в явном виде  получим
получим  , т.е.
, т.е.  ,
,  ,
,  ,
,  , поэтому
, поэтому  ,
,  ,
,  , и
, и  . Мы уже пользовались этой формулой при вычислении площади поверхности с помощью двойного интеграла.
. Мы уже пользовались этой формулой при вычислении площади поверхности с помощью двойного интеграла.
 16.4.3.3.2. Выражение поверхностного интеграла через двойной интеграл по проекции поверхности на координатную плоскость. Пусть поверхность
16.4.3.3.2. Выражение поверхностного интеграла через двойной интеграл по проекции поверхности на координатную плоскость. Пусть поверхность  взаимно однозначно проецируется в область
взаимно однозначно проецируется в область  на плоскости Оху. Будем считать, что поверхность задана уравнением
на плоскости Оху. Будем считать, что поверхность задана уравнением  ,
,  . В интегральной сумме
. В интегральной сумме  выразим площадь
выразим площадь  через двойной интеграл по её проекции
через двойной интеграл по её проекции  на плоскость Оху:
на плоскость Оху:  . Применим к этому интегралу теорему о среднем: существует точка
. Применим к этому интегралу теорему о среднем: существует точка  такая, что
такая, что  . Значение подынтегральной функции
. Значение подынтегральной функции  будем вычислять в точке
будем вычислять в точке  , такой, что
, такой, что  . Тогда
. Тогда  .
.
Слева стоит интегральная сумма для поверхностного интеграла, справа - для двойного; переход к пределу при  (при этом и
(при этом и  ) даёт
) даёт
 .
.
Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Примеры. 1. Найти  , где s - часть цилиндра x2 + z2 = 2x, вырезаемая гиперболоидом x2 - y2 + z2 = 1 и плоскостью z = 0 (z > 0).
, где s - часть цилиндра x2 + z2 = 2x, вырезаемая гиперболоидом x2 - y2 + z2 = 1 и плоскостью z = 0 (z > 0).
Решение: Найдем проекцию поверхности s на плоскость OXY. Исключим из уравнений цилиндра и гиперболоида переменную z:
 2x = y2+1 - уравнение проекции линии пересечения двух поверхностей на OXY.
2x = y2+1 - уравнение проекции линии пересечения двух поверхностей на OXY. 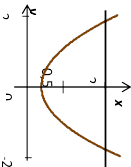
Полагая в уравнении цилиндра z = 0, получим уравнение линии пересечения цилиндра и плоскости OXY. Таким образом, поверхность s проецируется в область D, ограниченную параболой x = (y2+1) и прямой x=2. Часть цилиндра, удовлетворяющая условию z>0, задается уравнением z =
(y2+1) и прямой x=2. Часть цилиндра, удовлетворяющая условию z>0, задается уравнением z =  . Тогда
. Тогда 
 =
=  =
= . Таким образом,
. Таким образом, 

 .
.

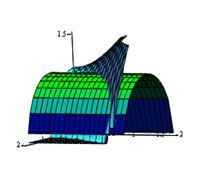
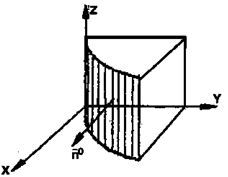
2. Найти  , где s - полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤ 1.
, где s - полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤ 1.
Решение: Искомый интеграл равен сумме трех интегралов: по нижнему и верхнему основаниям s1 и s2 и боковой поверхности (рис.18). Так как на нижнем основании z=0, то  =0. Для верхнего основания s2 имеем z(x,y)=1,
=0. Для верхнего основания s2 имеем z(x,y)=1,  =
= =0, поэтому поверхностный интеграл по s2 совпадает с двойным интегралом от функции z(x,y)|xy| = |xy|, взятым по кругу D ={x2+ y2<1}:
=0, поэтому поверхностный интеграл по s2 совпадает с двойным интегралом от функции z(x,y)|xy| = |xy|, взятым по кругу D ={x2+ y2<1}:
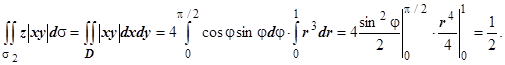
Найдем интеграл по боковой поверхности. Она состоит из двух частей: s3 и s4 , симметричных относительно плоскости OYZ. Так как функция z|xy| - четная по x, то интегралы по s3 и s4 равны.
Проекция s3 на плоскость OYZ - прямоугольник D:{-1 ≤ у ≤ 1, 0 ≤ z ≤1}. Уравнение s3 : х=
 Отсюда:
Отсюда: 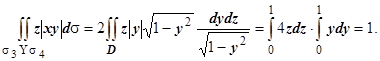
Окончательно получаем: 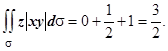
3. Найти  , где s - сфера x2 + y2 + z2 = R2.
, где s - сфера x2 + y2 + z2 = R2.
Решение: Использование соображений симметрии позволяет иногда существенно упростить вычисление интегралов. Очевидно, что для сферы  . Тогда
. Тогда
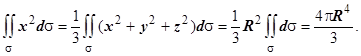
6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.
6.4.3.4.1. Масса поверхности. Пусть на поверхности s распределена масса с поверхностной плотностью m(x,y,z). Тогда масса m поверхности равна
m =  .
.
6.4.3.4.2. Статические моменты и центр масс. Статические моменты поверхности относительно координатных плоскостей OYZ, OXZ, OXY равны соответственно 

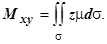
Координаты центра масс поверхности s равны xc =  , yc =
, yc =  , zc =
, zc =  .
.
6.4.3.4. 3. Моменты инерции. Момент инерции поверхности s относительно прямой L равен IL= , где
, где  =rL(x,y,z) - расстояние от точки (x,y,z), лежащей на поверхности s, до прямой L. В частности, моменты инерции относительно координатных осей OX, OY, OZ равны
=rL(x,y,z) - расстояние от точки (x,y,z), лежащей на поверхности s, до прямой L. В частности, моменты инерции относительно координатных осей OX, OY, OZ равны
 ,
,  ,
,  .
.
Момент инерции относительно точки P(x0,y0,z0) равен
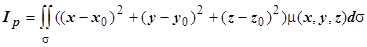
Момент инерции относительно начала координат равен
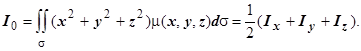
Пример. Найти координаты центра масс полусферы x2 + y2 + z2 = R2, z £ 0, если поверхностная плотность в каждой точке сферы равна расстоянию от этой точки до оси OZ.
Решение: Масса полусферы s равна
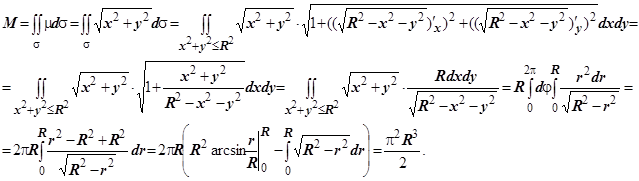
(Мы воспользовались тем, что интеграл  равен четверти площади круга радиуса R т.е.
равен четверти площади круга радиуса R т.е.  ).
).
16.4.4. Поверхностный интеграл второго рода (по координатам).

16.4.4.1. Определение поверхностного интеграла второго рода. Пусть в пространстве переменных x,y,z задана ограниченная кусочно-гладкая двусторонняя поверхность , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке
, на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке  задана сторона поверхности), и на которой определена функция R(x,y,z). Разобьём поверхность на
задана сторона поверхности), и на которой определена функция R(x,y,z). Разобьём поверхность на  частей
частей  , на каждой из частей
, на каждой из частей  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  , нормаль
, нормаль  в точке
в точке  к выбранной стороне поверхности, и площадь
к выбранной стороне поверхности, и площадь  проекции части
проекции части  на плоскость ОХУ. В интегральную сумму слагаемое
на плоскость ОХУ. В интегральную сумму слагаемое  возьмём со знаком "+", если
возьмём со знаком "+", если  (т.е. если угол
(т.е. если угол  между
между  и осью Oz - острый; проекция
и осью Oz - острый; проекция  на орт
на орт  оси Oz положительна), и со знаком "-", если
оси Oz положительна), и со знаком "-", если  . В результате интегральная сумма будет иметь вид
. В результате интегральная сумма будет иметь вид  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности  на части
на части  , ни от выбора точек
, ни от выбора точек  , то функция R(x,y,z) называется интегрируемой по поверхности
, то функция R(x,y,z) называется интегрируемой по поверхности  , а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х,у, и обозначается
, а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х,у, и обозначается  .
.
Теорема существования. Если функция R(x,y,z) непрерывна на поверхности  , то она интегрируема по этой поверхности.
, то она интегрируема по этой поверхности.
Если на поверхности  , вместе с функцией R(x,y,z), определены функции P(x,y,z) и Q(x,y,z), то, так же, как и интеграл
, вместе с функцией R(x,y,z), определены функции P(x,y,z) и Q(x,y,z), то, так же, как и интеграл  , определяются интегралы
, определяются интегралы  и
и  ; в приложениях, как мы видели из рассмотренной в начале раздела физической задачи, обычно рассматривается сумма этих интегралов, которая обозначается
; в приложениях, как мы видели из рассмотренной в начале раздела физической задачи, обычно рассматривается сумма этих интегралов, которая обозначается  .
.
16.4.4.2. Свойства поверхностного интеграла второго рода. Для этого интеграла, как и для криволинейного интеграла второго рода, имеет смысл формулировать следующие свойства: линейность, аддитивность и зависимость поверхностного интеграла от выбора стороны поверхности: при изменении ориентации поверхности интеграл меняет знак.
16.4.4.3. Вычисление поверхностного интеграла второго рода. Пусть поверхность  взаимно однозначно проецируется в область
взаимно однозначно проецируется в область  на плоскости Оху. В этом случае
на плоскости Оху. В этом случае  имеет одинаковый знак во всех точках поверхности. Именно,
имеет одинаковый знак во всех точках поверхности. Именно,  , если рассматривается верхняя сторона поверхности, и
, если рассматривается верхняя сторона поверхности, и  , если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид
, если рассматривается нижняя сторона. Поэтому для верхней стороны все слагаемые в интегральной сумме должны браться со знаком "+", и сумма будет иметь вид  . Если поверхность задана уравнением
. Если поверхность задана уравнением  ,
,  , то эта сумма равна
, то эта сумма равна  . В последней сумме легко увидеть интегральную сумму для двойного интеграла
. В последней сумме легко увидеть интегральную сумму для двойного интеграла  . Переход к пределу при
. Переход к пределу при  (при этом и
(при этом и  ) даст
) даст
 . Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид
. Напомню, что эта формула получена для верхней стороны поверхности. Если выбрана нижняя сторона, то все слагаемые в интегральной сумме должны браться со знаком "-", и интегральная сумма будет иметь вид  . Рассуждая, как и для верхней стороны, получим, что в этом случае
. Рассуждая, как и для верхней стороны, получим, что в этом случае  . Окончательно,
. Окончательно,  , где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
, где знак "+" берётся для верхней стороны поверхности, знак "-" - для нижней стороны.
Аналогично изложенному, для других интегралов:  , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где
на плоскости Oyz, при этом знак "+" берётся для "передней" стороны поверхности (где  ), для "задней" стороны, где
), для "задней" стороны, где  , берётся знак "-";
, берётся знак "-";  , если поверхность однозначно проецируется в область
, если поверхность однозначно проецируется в область  на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где
на плоскость Oхz, знак "+" берётся для "правой" стороны поверхности (где  ), для "левой" стороны, где
), для "левой" стороны, где  , берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
, берётся знак "-". Как и для поверхностного интеграла первого рода, если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Примеры. 1. Вычислить  , s - часть поверхности цилиндра y =
, s - часть поверхности цилиндра y =  , заключенная между плоскостями x=0, x=8, z=0, z=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
, заключенная между плоскостями x=0, x=8, z=0, z=3. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oх.
Решение: Определяем знаки направляющих косинусов нормали cosa>0, cosb<0, cosg=0. Поэтому

 , где
, где
Dyz={(y,z): 0£ y £16, 0 £ z £ 3}, Dxz={(x,z): 0 £ x £ 8, 0 £ z £ 3} - проекции s на плоскости Oyz и Oxz соответственно. Проекция поверхности s на плоскость Oxy вырождается в линию - параболу y= , cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz , выражая x(y,z) и y(x,z) из уравнения поверхности s: x(y,z)=2
, cosg=0, поэтому интеграл по Dxy в данном случае отсутствует. Вычислим отдельно интегралы по Dyz и Dxz , выражая x(y,z) и y(x,z) из уравнения поверхности s: x(y,z)=2 , y(x,z)=
, y(x,z)= .
.
 =
= =
= dy=328,
dy=328, =
= =
= dx=928. Окончательно I = 328 - 928 = - 600.
dx=928. Окончательно I = 328 - 928 = - 600.
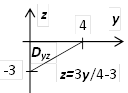
2. Вычислить  , где s - часть плоскости
, где s - часть плоскости  , ограниченная координатными плоскостями x=0, у=0, z=0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
, ограниченная координатными плоскостями x=0, у=0, z=0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
Решение. Из двух направлений нормали к s  мы должны выбрать такое, для которого коэффициент при орте
мы должны выбрать такое, для которого коэффициент при орте  (т.е.
(т.е.  ) положителен, поэтому выбираем знак "-", тогда
) положителен, поэтому выбираем знак "-", тогда  . В соответствии со знаками направляющих косинусов,
. В соответствии со знаками направляющих косинусов, 
 . Вычисляем эти интегралы.
. Вычисляем эти интегралы.
1. 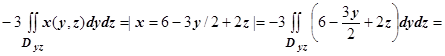
 .
.
Если Вам понравилась эта лекция, то понравится и эта - 5.1. Язык карты. Картографические знаки.
2.  .
.
3. 
 . Окончательно,
. Окончательно, 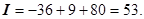
В заключение напомню, что вычисление поверхностного интеграла второго рода всегда можно свести к вычислению поверхностного интеграла первого рода. Так, в последнем примере подынтегральное выражение равно  , где
, где  ,
, 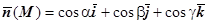
 . Поэтому
. Поэтому  , и, проектируя s на плоскость Оху
, и, проектируя s на плоскость Оху  , получим
, получим 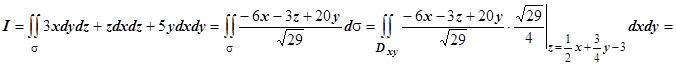
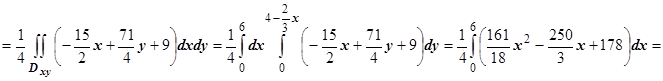
 .
.




















