Слабая сходимость
§9. Слабая сходимость.
Понятие слабой сходимости является важнейшим инструментом при доказательстве теорем существования решений дифференциальных уравнений.
Определение 1.
Последовательность  векторов гильбертова пространства
векторов гильбертова пространства  называется слабо сходящейся к вектору
называется слабо сходящейся к вектору  если
если  .
.
Слабая сходимость обозначается знаком  при
при  .
.
Ниже мы докажем, что всякая слабо сходящаяся последовательность ограничена. Отметим, что ограниченность последовательности векторов  равносильна неравенствам
равносильна неравенствам  .
.
Здесь мы использовали обозначение  для шара радиуса
для шара радиуса  с центром в точке
с центром в точке  .
.
Лемма 1.
Если последовательность  не ограничена, то
не ограничена, то  найдется вектор
найдется вектор  и натуральное
и натуральное  такие, что
такие, что  .
.
Рекомендуемые материалы
Доказательство от противного.
Пусть  , такие, что при любом
, такие, что при любом  и любом
и любом  выполнены неравенства
выполнены неравенства  . Тогда при любом
. Тогда при любом  и любом
и любом 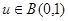
 .
.
Здесь мы воспользовались тем, что  . Последнее неравенство противоречит неограниченности последовательности
. Последнее неравенство противоречит неограниченности последовательности  . Лемма доказана.
. Лемма доказана.
Теорема 1. (Теорема Банаха-Штейнгауза).
Слабо сходящаяся последовательность векторов ограничена.
Доказательство от противного.
По лемме для  найдется номер
найдется номер  и вектор
и вектор  такие, что
такие, что  . По непрерывности функционала
. По непрерывности функционала  найдется шар
найдется шар  такой, что
такой, что  .
.
Далее, для  найдется номер
найдется номер  и вектор
и вектор  такие,
такие,
что  . По непрерывности функционала
. По непрерывности функционала  найдется шар
найдется шар  такой, что
такой, что  .
.
Продолжая процесс, получим последовательность вложенных шаров  , имеющую хотя бы одну общую точку
, имеющую хотя бы одну общую точку  . Тогда
. Тогда  , что противоречит ограниченности сходящейся последовательности
, что противоречит ограниченности сходящейся последовательности  . Теорема доказана.
. Теорема доказана.
Лемма 2.
Пусть последовательность  ограничена. Пусть линейная оболочка векторов
ограничена. Пусть линейная оболочка векторов  плотна в
плотна в  . Пусть
. Пусть  , тогда
, тогда  слабо.
слабо.
Доказательство.
Пусть  – произвольный вектор из линейной оболочки,
– произвольный вектор из линейной оболочки,  , тогда
, тогда
 =
= .
.
Если теперь  произвольный вектор, то в силу плотности линейной оболочки найдется вектор
произвольный вектор, то в силу плотности линейной оболочки найдется вектор  такой, что
такой, что  . В силу ограниченности
. В силу ограниченности  ,
, По определению предела, найдется
По определению предела, найдется  такое, что при
такое, что при  выполнено неравенство
выполнено неравенство  .
.
Имеем 

Это означает, что  .
.
Лемма доказана.
Лемма 3.
Если  слабо,
слабо,  сильно, то
сильно, то  .
.
Доказательство, благодаря ограниченности последовательности  , аналогично доказательству леммы 2.
, аналогично доказательству леммы 2.
Теорема 2.
Из ограниченной последовательности векторов гильбертова пространства можно выделить слабо сходящуюся подпоследовательность.
Доказательство проведем для случая сепарабельного гильбертова пространства. Общий случай сводится к этому взятием линейной оболочки
исходной последовательности.
Пусть  – счетное всюду плотное множество в
– счетное всюду плотное множество в  . Пусть
. Пусть  заданная ограниченная последовательность. Тогда числовая последовательность
заданная ограниченная последовательность. Тогда числовая последовательность  ограничена и из нее можно выделить сходящуюся числовую подпоследовательность
ограничена и из нее можно выделить сходящуюся числовую подпоследовательность  . Для удобства векторы
. Для удобства векторы  переобозначим так:
переобозначим так:  . Далее числовая последовательность
. Далее числовая последовательность  также ограничена и из нее можно выделить сходящуюся числовую подпоследовательность
также ограничена и из нее можно выделить сходящуюся числовую подпоследовательность  . Для удобства векторы
. Для удобства векторы  переобозначим так:
переобозначим так:  . Процесс продолжается бесконечно. Возьмем диагональную последовательность
. Процесс продолжается бесконечно. Возьмем диагональную последовательность  . По построению она обладает свойством:
. По построению она обладает свойством:  . Поэтому она сходится на любом векторе
. Поэтому она сходится на любом векторе  , то есть существует предел
, то есть существует предел
 . (1)
. (1)
Убедимся, что на самом деле существует предел при любом  . Выберем
. Выберем  так, чтобы
так, чтобы  . Тогда, в силу (1), выполнен критерий Коши:
. Тогда, в силу (1), выполнен критерий Коши:  .Поэтому
.Поэтому

 .
.
Таким образом, выполнен критерий Коши, обеспечивающий существование предела  . Теперь положим по определению
. Теперь положим по определению  .
.
Легко проверить, что  – линейный ограниченный функционал. По теореме Рисса существует
– линейный ограниченный функционал. По теореме Рисса существует  . Теорема доказана.
. Теорема доказана.
Далее понадобится понятие сопряженного оператора.
Определение 2.
Пусть  – ограниченные операторы в гильбертовых пространствах над полем
– ограниченные операторы в гильбертовых пространствах над полем  . Если
. Если  , то эти операторы называются взаимно сопряженными:
, то эти операторы называются взаимно сопряженными:  .
.
Утверждение.
Всякий ограниченный оператор имеет сопряженный оператор.
Доказательство.
 является линейным непрерывным функционалом на
является линейным непрерывным функционалом на  , поскольку
, поскольку  .
.
По теореме Рисса найдется единственный вектор  такой, что
такой, что
 . Тем самым определено отображение
. Тем самым определено отображение  .
.
Поопределению,
 . (2)
. (2)
Остается проверить, что оператор  – линейный и непрерывный.
– линейный и непрерывный.
Имеем 
 .
.
Отсюда получаем  , что и означает линейность оператора
, что и означает линейность оператора  . Установим его ограниченность. Подставим в формулу (2)
. Установим его ограниченность. Подставим в формулу (2)  . Тогда
. Тогда  . Отсюда
. Отсюда  . Что и требовалось. Более того, мы доказали равенство
. Что и требовалось. Более того, мы доказали равенство  .
.
Теорема 3.
Компактный оператор слабо сходящуюся последовательность переводит в сходящуюся последовательность.
Доказательство.
Пусть  – компактный линейный оператор и
– компактный линейный оператор и  слабо в пространстве
слабо в пространстве  .
.
По теореме1 множество  ограничено. Поэтому множество
ограничено. Поэтому множество  – компактное. Из него можно выделить фундаментальную подпоследовательность
– компактное. Из него можно выделить фундаментальную подпоследовательность  . Тогда существует предел
. Тогда существует предел  . Докажем, что
. Докажем, что  . Имеем
. Имеем
 . Отсюда
. Отсюда  .
.
Установим теперь, что  . В ином случае найдется
. В ином случае найдется  и подпоследовательность
и подпоследовательность  такая, что
такая, что  . Это противоречит выше изложенному. Теорема доказана.
. Это противоречит выше изложенному. Теорема доказана.
В следующей теореме возьмем  – произвольная ограниченная область,
– произвольная ограниченная область,  – оператор вложения.
– оператор вложения.
Теорема 4.
Если  слабо в пространстве
слабо в пространстве  , то
, то  сильно в
сильно в 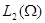 и
и  слабо в
слабо в 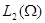 . (
. ( − ограниченная область).
− ограниченная область).
Доказательство.
Сходимость  следует из теоремы 3 и компактности оператора
следует из теоремы 3 и компактности оператора
вложения. Из ограниченности последовательности  в пространстве
в пространстве 
следует ограниченность  в
в 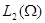 . Тогда можно выделить слабо сходящуюся в
. Тогда можно выделить слабо сходящуюся в 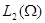 подпоследовательность
подпоследовательность  при
при  .
.
Поэтому для функции  имеем
имеем
 .
.
Отсюда заключаем, что  . Покажем, что на самом деле вся последовательность слабо сходится
. Покажем, что на самом деле вся последовательность слабо сходится  при
при  . Если предположить противное, то найдется
. Если предположить противное, то найдется  такая, что
такая, что  . Тогда найдется подпоследовательность
. Тогда найдется подпоследовательность  такая, что
такая, что  . Тогда из нее нельзя выделить подпоследовательность, слабо сходящуюся к
. Тогда из нее нельзя выделить подпоследовательность, слабо сходящуюся к  , что противоречит вышеизложенному. Теорема доказана.
, что противоречит вышеизложенному. Теорема доказана.
Теорема 5.
Вам также может быть полезна лекция "16 Надежность отказоустойчивых систем (ОУС)".
Если  слабо в пространстве
слабо в пространстве  , где
, где  – произвольная область, то
– произвольная область, то  в
в 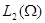
 и
и  в
в 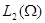 .
.
Доказательство.
Пусть шар  . Выберем
. Выберем  так, чтобы
так, чтобы  . Пусть
. Пусть  – срезающая функция, равная 1 в шаре
– срезающая функция, равная 1 в шаре  . Тогда
. Тогда  – ограниченная последовательность в пространстве
– ограниченная последовательность в пространстве  . По теореме 2 можно выделить слабо сходящуюся подпоследовательность
. По теореме 2 можно выделить слабо сходящуюся подпоследовательность  при
при  . По теореме 4 имеем сильную сходимость
. По теореме 4 имеем сильную сходимость  в
в  и слабые сходимости
и слабые сходимости  в
в  . Поскольку
. Поскольку  в
в  , то отсюда следует, что
, то отсюда следует, что  в
в  и
и  в
в  . Далее, выбирая подпоследовательности, можно добиться, чтобы
. Далее, выбирая подпоследовательности, можно добиться, чтобы  в
в  и
и  в
в  для любой ограниченной области
для любой ограниченной области  такой, что
такой, что  .
.
Поскольку  , то фактически
, то фактически  . Аналогично,
. Аналогично,  и по теореме Лебега об ограниченной сходимости
и по теореме Лебега об ограниченной сходимости  в
в 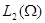 . Далее, функции из
. Далее, функции из  образуют плотное множество в
образуют плотное множество в  , поэтому из леммы 2 следует слабая сходимость
, поэтому из леммы 2 следует слабая сходимость  в
в  . Имеем
. Имеем
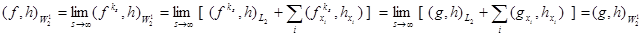
Если  , то отсюда заключаем, что
, то отсюда заключаем, что  .
.





















