Температурный режим газопровода
III ТЕМПЕРАТУРНЫЙ РЕЖИМ ГАЗОПРОВОДА
Температура движущегося в трубопроводе газа зависит от физических условий движения и от теплообмена с окружающей средой. Для решения задачи привлечем уравнение первого начала термодинамики:
 ,
,
где  – количество подведенной теплоты;
– количество подведенной теплоты;  – изменение внутренней энергии газа; р – давление; υ – удельный объем газа;
– изменение внутренней энергии газа; р – давление; υ – удельный объем газа;  – работа, совершаемая газом.
– работа, совершаемая газом.
Количество теплоты  складывается из подведенной теплоты извне (
складывается из подведенной теплоты извне ( ) и выделившейся в результате трения (
) и выделившейся в результате трения ( ). Для газа, движущегося в трубопроводе, теплота, подведенная извне на участке
). Для газа, движущегося в трубопроводе, теплота, подведенная извне на участке  ,
,
 ,
,
где  – коэффициент теплопередачи от газа в окружающую среду;
– коэффициент теплопередачи от газа в окружающую среду;  – диаметр трубопровода;
– диаметр трубопровода;  – температура газа в сечении
– температура газа в сечении  ,
,  – температура окружающей среды;
– температура окружающей среды;  – массовый расход.
– массовый расход.
Представив работу  в виде
в виде  –
–  , где
, где  – плотность газа, получим
– плотность газа, получим
Рекомендуемые материалы
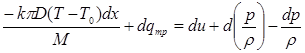
и далее, поскольку  – энтальпия,
– энтальпия,
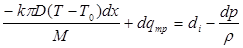
Заметим здесь, что теплота  , выделившаяся на участке
, выделившаяся на участке  , равна
, равна  и что этой же величине равно и
и что этой же величине равно и  (если пренебречь изменением кинетической энергии и влиянием силы тяжести). Следовательно,
(если пренебречь изменением кинетической энергии и влиянием силы тяжести). Следовательно,  и
и  сократятся. Это формально. Физический смысл в том, что работа, затраченная газом на преодоление трения, тотчас же возвращается газу в виде теплоты dqтр. Компенсация работы трения выделившейся теплотой – внутренний процесс, а рассматриваемое уравнение выражает собой баланс энергии между газом и окружающей средой. Поэтому в нем не должно быть ни работы трения, ни теплоты трения. Итак, получим
сократятся. Это формально. Физический смысл в том, что работа, затраченная газом на преодоление трения, тотчас же возвращается газу в виде теплоты dqтр. Компенсация работы трения выделившейся теплотой – внутренний процесс, а рассматриваемое уравнение выражает собой баланс энергии между газом и окружающей средой. Поэтому в нем не должно быть ни работы трения, ни теплоты трения. Итак, получим
 (1)
(1)
Теперь учтем, что энтальпия – функция температуры и давления  и, следовательно,
и, следовательно,
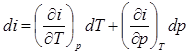
Вспомним, что  – теплоемкость при постоянном давлении. Что представляет собой
– теплоемкость при постоянном давлении. Что представляет собой  , выясним, предположив, что i – постоянная величина. В этом случае
, выясним, предположив, что i – постоянная величина. В этом случае
 .
.
Отсюда получаем, что
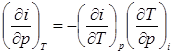
Но  – коэффициент Джоуля – Томсона. Следовательно,
– коэффициент Джоуля – Томсона. Следовательно,  и, далее,
и, далее,  .
.
Введем это в уравнение (1) и разделим его на  :
:
 .
.
Теперь представим  в виде
в виде  и примем, что градиент падения давления
и примем, что градиент падения давления  (линейный закон распределения давления). Затем, обозначив для краткости
(линейный закон распределения давления). Затем, обозначив для краткости  , будем иметь
, будем иметь
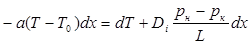
и далее
 .
.
После интегрирования получаем следующую формулу, определяющую температуру газа на расстоянии  от начальной точки газопровода:
от начальной точки газопровода:
 . (2)
. (2)
Если здесь отбросить последнее слагаемое, то получим знаменитую формулу Шухова
 (3)
(3)
Формула Шухова описывает распределение температуры по длине трубопровода, обусловленное теплопередачей в окружающую среду. Согласно (3) при  температура газа
температура газа  в любой точке газопровода больше
в любой точке газопровода больше  . Лишь при
. Лишь при 
 .
.
В формуле (2) последнее слагаемое учитывает понижение температуры из-за эффекта Джоуля — Томсона. Этой формулой следует пользоваться, когда требуется повышенная точность расчета.
На основании (2) и (3) получаются следующие формулы для вычисления средней температуры газа по длине трубопровода:
 (4)
(4)
Бесплатная лекция: "12 Построение общего решения линейного однородного дифференциального уравнения n-го порядка" также доступна.
и
 . (5)
. (5)
Температура газа, входящая в формулы для гидравлического расчета газопровода, принимается равной  . На рис. 1 изображен график, показывающий характер изменения температуры по длине газопровода.
. На рис. 1 изображен график, показывающий характер изменения температуры по длине газопровода.
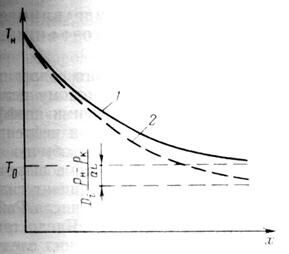
Рис. 1. Кривые изменения температуры газа по длине газопровода:
1 – по Шухову; 2 – с учетом эффекта Джоуля–Томсона




















