Математическое описание процессов преобразования энергии в асинхронном двигателе
Математическое описание процессов преобразования энергии в асинхронном двигателе.
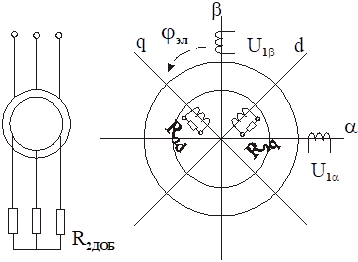
Схема включения АД с фазным ротором и соответствующая ей схема двухфазной модели изображены на рисунках.
Математическое описание процессов эл.механического преобразования энергии в осях a и b можно получить из ранее приведенных уравнений положив в них U2=0 и wк=0.
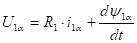
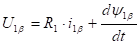
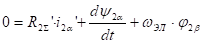
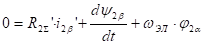
, где 
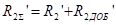
Рекомендуемые материалы
Эти уравнения используются для анализа динамических свойств асинхронного ЭМП. В установившемся симметричном режиме работы двигателя переменные представляют собой сдвинутые относительно друг от друга по фазе синусоидальные величины, изменяющиеся в осях a, b с частотой сети: 
.
Представим эти переменные в виде вращающихся векторов U1a, I1a, U1b, I1b и т.д. Т.к. переменные фазы a отстают от переменных фазы b на jэл=90°, между ними очевидна связь: 
и .т.д. Учитывая это и имея ввиду, что производная по времени от вектора, неизменного по модулю и вращающегося со скоростью w0эл, может быть получена умножением этого вектора на jw0эл, т.е. например: 
, уравнения электрического равновесия для фазы a статора и ротора можно представить в виде:
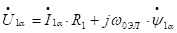
, т.к.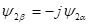 
Для анализа статических режимов преобразования энергии выразим потокосцепления Y1 и Y2 через намагничивающий ток: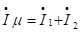 
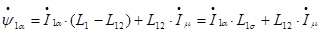
т.о.
и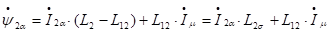 
Где L1s и L2s - индуктивности рассеяния статорной и роторной обмоток. Параметры L1, L2,L12 двухфазной модели выразим через каталожные параметры реального трехфазного двигателя с помощью соотношений: 
; 
; 
, а с помощью ранее полученных формул обратного преобразования заменим переменные двухфазной модели соответствующими эффективными значениями переменных трехфазного двигателя. Тогда уравнения электрического равновесия примут вид:
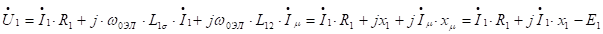
Информация в лекции "Психология педагогического общения" поможет Вам.
.
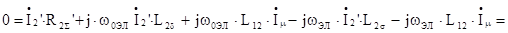
Поделив обе части на 
, получим
, или 
,
где 
; 
; 
; 
; 
 |
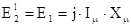
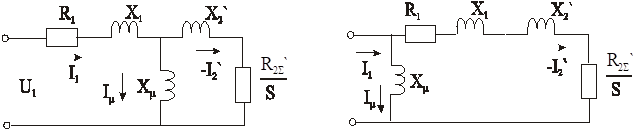Этим уравнениям соответствует Т-образная схема замещения, известная из курса эл.машин и упрощенная Г-образная схема.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
