Моделирование дискретных технологических процессов
5 – Моделирование дискретных технологических процессов. Сети Петри.
Применяются сети Петри исключительно в моделировании. Во многих областях исследований явление изучается не непосредственно, а косвенно, через модель. Модель – это представление, как правило, в математических терминах того, что считается наиболее характерным в изучаемом объекте или системе. Ожидается, что, манипулируя представлением, можно получить новые знания о моделируемом явлении, избегая опасности, дороговизну или неудобства манипулирования самим реальным явлением.
Как правило, модели имеют математическую основу. Характеристики многих физических явлений можно описать числами, а связь этих характеристик – уравнениями или неравенствами. В частности, в естественных науках и технике уравнениями описываются такие характеристики, как масса, положение в пространстве, момент, ускорение и силы. Однако для успешного использования подхода моделирования необходимо знание как моделируемых явлений, так и свойств метода моделирования. Поэтому математика как наука развивалась частично благодаря использованию ее в моделировании явлений, изучаемых другими науками.
С разработкой быстродействующих ЭВМ использование и полезность моделирования значительно возросли. Представление системы математической моделью, преобразование этой модели в команды на ЭВМ и выполнение программы на ЭВМ сделали возможным моделирование больших и более сложных систем, чем ранее. Это привело в результате к значительным исследованиям методов моделирования на ЭВМ и самих ЭВМ, поскольку они участвуют в моделировании в двух ролях: как вычислительные средства и как объект моделирования.
Вычислительные системы очень сложны, часто велики, включают множество взаимодействующих компонент. Каждая компонента также может быть очень сложной, поскольку взаимодействует с другими компонентами системы. Это справедливо и для многих других систол. Экономические системы, юридические системы, системы управления дорожным движением, химические системы состоят из многих отдельных компонент, взаимодействующих друг с другом -ложным образом.
Зарождение теории сетей Петри
Сети Петри разрабатывались специально для моделирования тех систем, которые содержат взаимодействующие параллельные компоненты. Впервые сети Петри предложил Карл Адам Петри. В своей докторской диссертации «Kommunikation mit Automaten» («Связь автоматов») Петри сформулировал основные понятия теории связи асинхронных компонент вычислительной системы. В частности, он подробно рассмотрел описание причинных связей между событиями. Его диссертация посвящена главным образом теоретической разработке основных понятий, с которых начали развитие сети Петри.
Рекомендуемые материалы
Возможно несколько путей практического применения сетей Петри при проектировании и анализе систем. В одном из подходов сети Петри рассматриваются как вспомогательный инструмент анализа. Здесь для построения системы используются общепринятые методы проектирования. Затем построенная система моделируется сетью Петри, и модель анализируется. Любые трудности, встречающиеся при анализе, указывают на изъяны в проекте. Для их исправления необходимо модифицировать проект. Модифицированный проект затем снова моделируется и анализируется. Этот цикл повторяется до тех пор, пока проводимый анализ не приведет к успеху. Заметим, что этот подход можно использовать и для анализа уже существующих действующих в настоящее время систем.
В этом общепринятом подходе использования сетей Петри в проектировании требуется постоянное преобразование проектируемой системы в модель в виде сети Петри. Можно предложить другой, более радикальный подход, в котором весь процесс проектирования и определения характеристик проводится в терминах сетей Петри. Методы анализа применяются только для создания проекта сети Петри, свободного от ошибок. Здесь задача заключается в преобразовании представления сети Петри в реальную рабочую систему.
Эти два подхода использования сетей Петри в процессе проектирования предлагают исследователю сетей Петри задачи разного типа. В первом случае необходима разработка методов моделирования систем сетями Петри, а во втором случае должны быть разработаны методы реализации сетей Петри системами. В обоих случаях необходимы методы анализа сетей Петри для определения свойств модели. Таким образом, первое, чего нам необходимо коснуться при рассмотрении теории сетей Петри, — это изучение свойств самих сетей Петри.
Структура сети Петри
Сеть Петри состоит из четырех элементов: множество позиций Р, множество переходов Т, входная функция I и выходная функция О. Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход tj в множество позиций I(tj), называемых входными позициями перехода. Выходная функция О отображает переход tj в множество позиций O(tj), называемых выходными позициями перехода.
Структура сети Петри определяется ее позициями, переходами, входной и выходной функциями.
Определение 1. Сеть Петри С является четверкой, С= (Р, Т, I, О). Р= {р1, р2, ..., рn} – конечное множество позиций, n³0. Т={t1, t2, ..., tm} – конечное множество переходов, m³0. Множество позиций и множество переходов не пересекаются, Р Ç Т = Æ. I: Т®Р является входной функцией – отображением из переходов в комплекты позиций. О: Т® Р есть выходная функция – отображение из переходов в комплекты позиций.
Мощность множества Р есть число n, а мощность множества Т есть число m. Произвольный элемент Р обозначается символом рi, i=1, ..., п, а произвольный элемент Т – символом tj, j=1,..., m.
Позиция рi является входной позицией перехода tj в том случае, если piÎI(tj), pi является выходной позицией, если piÎO(tj). Входы и выходы переходов представляют собой комплекты позиций. Комплект является обобщением множества, в которое включены многократно повторяющиеся элементы – тиражированные элементы. В приложении 1 содержится описание теории комплектов. Использование комплектов, а не множеств для входов и выходов перехода позволяет позиции быть кратным входом либо кратным ' выходом перехода. Кратность входной позиции pi для перехода tj есть число появлений позиции во входном комплекте перехода, #(pi,I(tj)). Аналогично кратность выходной позиции pi для перехода tj есть число появлений позиции в выходном комплекте перехода, #(pi,O(tj)). Если входная и выходная функции являются множествами (а не комплектами), то кратность каждой позиции есть либо 0, либо 1.
Входные и выходные функции используются для отображения позиций в комплекты переходов, а также их можно использовать для отображения переходов в комплекты позиций. Определим, что переход tj является входом позиции pi, если pi есть выход tj. Переход tj есть выход позиции pi, если pi есть вход tj.
Определение 2. Определим расширенную входную функцию I и выходную функцию 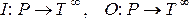 таким образом, что #(tj, I(pi)) = #(pi, I(tj)), #(tj, O(pi)) = # (pi, I(tj)).
таким образом, что #(tj, I(pi)) = #(pi, I(tj)), #(tj, O(pi)) = # (pi, I(tj)).
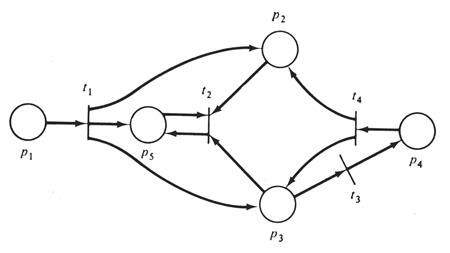
Пример.
I(p1)={ }, O(p1)={t1},
I(p2)={t1,t4 }, O(p2)={t2},
I(p3)={t1,t4 }, O(p3)={t2,t3},
I(p4)={t3 }, O(p4)={t4},
I(p5)={ t1,t2}, O(p5)={t2}.
C = (P, T, I, O),
P={p1, p2, p3, p4, p5},
T={t1, t2, t3, t4}.
I(t1)={p1 }, O(t1)={p2, p3, p4},
I(t2)={p2, p3, p4 }, O(t2)={p5},
I(t3)={p3 }, O(t3)={p4},
I(t4)={p4}, O(t4)={p2, p3}.
Рис.6.1. Структура сети Петри представлена в виде четверки, которая состоит из множества позиций (Р), множества переходов (Т), входной функции ( ) и выходной функции (
) и выходной функции ( )
)
Графы сетей Петри
В значительной степени теоретическая работа по сетям Петри основана на формальном определении сетей Петри, изложенном выше. Тем не менее для иллюстрации понятий теории сетей Петри гораздо более удобно графическое представление сети Петри. Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф.
Структура сети Петри представляет собой совокупность позиций и переходов. В соответствии с этим граф сети Петри обладает двумя типами узлов. Кружок О является позицией, а планка ½ – переходом.
Ориентированные дуги (стрелки) соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, а другие – от переходов к позициям. Дуга, направленная от позиции pi к переходу tj определяет позицию, которая является входом перехода. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выходная позиция указывается дугой от перехода к позиции. Кратные выходы также представлены кратными дугами.
Сеть Петри есть мультиграф, так как он допускает существование кратных дуг от одной вершины графа к другой. Следует добавить, что так как дуги являются направленными, то это ориентированный мультиграф. Мы знаем, что вершины графа можно разделить на два множества (позиции и переходы) таким образом, что каждая дуга будет направлена от элемента одного множества (позиций или переходов) к элементу другого множества (переходов или позиций); следовательно, такой граф является двудольным ориентированным мультиграфом. В дальнейшем для простоты будем называть его просто графом сети Петри.
Граф сети Петри, изображенный на рис.5.2, эквивалентен структуре сети Петри из выше приведенного примера.
|
Рис. 5.2 |
Для графов с большой кратностью используется пучок дуг, помеченный числом кратности, а не изображением кратных дуг (рис.5.3).
|
Рис. 5.3 |
Маркировка сетей Петри
Маркировка m есть присвоение фишек позициям сети Петри. Фишка – это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.
Определение 3. Маркировка m сети Петри С = (Р, Т, I, O) есть функция, отображающая множество позиций Р в множество неотрицательных целых чисел N:
m: P ® N
Маркировка m может быть также определена как n-вектор m = (m1, m2, ..., mn), где п =½P½ и каждое mi Î N, i=1,...,n. Вектор m определяет для каждой позиции pi сети Петри количество фишек в этой позиции. Количество фишек в позиции pi, есть mi, i=1,...,n. Связь между определениями маркировки как функции и как вектора очевидным образом устанавливается соотношением m(pi)=mi. Обозначение ее в виде функции является несколько более общим и поэтому употребляется гораздо чаще.
Маркированная сеть Петри М = (С, m) есть совокупность структуры сети Петри С = (Р, Т, I, O) и маркировки m и может быть записана в виде М = (Р, Т, I, O, m).
|
Рис.5.4. |
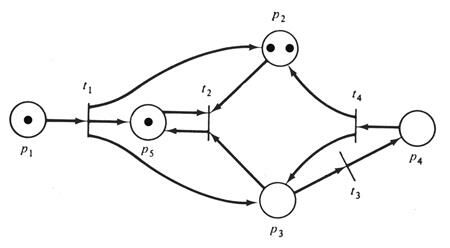
На графе сети Петри фишки изображаются маленькой точкой в кружке, который представляет позицию сети Петри. На рис.5.4 приведен пример графического представления маркированной сети Петри, аналогичной на рис.5.2 с маркировкой (1, 2, 0, 0, 1).
Так как количество фишек, которое может быть определено для каждой позиции, неограниченно, то в целом для сети Петри существует бесконечно много маркировок. Множество всех маркировок сети Петри, обладающей n позициями, есть множество всех n-векторов, Nn. Это множество, хотя и бесконечно, является счетным.
|
|
Рис.5.5 Граф сети Петри с очень большой маркировкой.
Правила выполнения сетей Петри
Выполнением сети Петри управляют количество и распределение фишек в сети. Фишки находятся в кружках и управляют выполнением переходов сети. Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.
Переход может запускаться только в том случае, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. Кратные фишки необходимы для кратных входных дуг. Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками. Например, если позиции p1 и p2 служат входами для перехода t4, тогда t4 разрешен, если p1 и p2 имеют хотя бы по одной фишке. Для перехода t7 с входным комплектом {p6, p6, p6} позиция p6 должна обладать по крайней мере тремя фишками, для того чтобы t7 был разрешен.
Определение 4. Переход tj Î T в маркированной сети Петри С = {Р, Т, I, O) с маркировкой m разрешен, если для всех pi Î P
 .
.
Переход запускается удалением всех разрешающих фишек из его входных позиций и последующим помещением в каждую из его выходных позиций по одной фишке для каждой дуги. Кратные фишки создаются для кратных выходных дуг. Переход t3 с O(t3)={p7, p13} и I(t3)={p2} разрешен всякий раз, когда в p2 будет хотя бы одна фишка. Переход t3 запускается удалением одной фишки из позиции p2 и помещением по одной фишки в позиции p7 и в p13 (его выходы). Дополнительные фишки в позиции p2 не влияют на запуск t3 (хотя они могут разрешать дополнительные запуски t3).
Запуск перехода в целом заменяет маркировку m сети Петри на новую маркировку 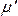 . Заметим также, что так как можно запустить только разрешенный переход, то при запуске перехода количество фишек в каждой позиции всегда остается неотрицательным. Запуск перехода никогда не удалит фишку, отсутствующую во входной позиции. Если какая-либо входная позиция перехода не обладает достаточным количеством фишек, то переход не разрешен и не может быть запущен.
. Заметим также, что так как можно запустить только разрешенный переход, то при запуске перехода количество фишек в каждой позиции всегда остается неотрицательным. Запуск перехода никогда не удалит фишку, отсутствующую во входной позиции. Если какая-либо входная позиция перехода не обладает достаточным количеством фишек, то переход не разрешен и не может быть запущен.
Определение 5. Переход tj маркированной сети Петри с маркировкой m может быть запущен всякий раз, когда он разрешен. В результате запуска разрешенного перехода tj образуется новая маркировка 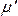 , определяемая следующим соотношением:
, определяемая следующим соотношением:  .
.
Пространство состояний сети Петри
Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т. е. Nn. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения d, которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке m (состоянию) и переходу tj, она образует новую маркировку (состояние), которая получается при запуске перехода tj в маркировке m. Так как tj может быть запущен только в том случае, когда он разрешен, то функция d(m, tj) не определена, если tj не разрешен в маркировке m. Если же tj разрешен, то  , где
, где 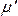 есть маркировка, полученная в результате удаления фишек из входов tj и добавления фишек в выходы tj.
есть маркировка, полученная в результате удаления фишек из входов tj и добавления фишек в выходы tj.
Определение 6. Функция следующего состояния d: Nn´T ® Nn для сети Петри С = (Р, Т, I, O) с маркировкой m и переходом tjÎT определена тогда и только тогда, когда m(pi) ³ #(pi, I(tj)) для всех pi Î P. Если d(m, tj) определена, то 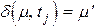 , где
, где 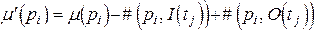 для всех piÎP.
для всех piÎP.
Пусть дана сеть Петри С = (Р, Т, I, O) с начальной маркировкой m. Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода tj в начальной маркировке образует новую маркировку  . В этой новой маркировке можно запустить любой другой разрешенный переход, например tk, образующий новую маркировку
. В этой новой маркировке можно запустить любой другой разрешенный переход, например tk, образующий новую маркировку 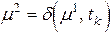 . Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.
. Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.
При выполнении сети Петри получаются две последовательности: последовательность маркировок  и последовательность переходов, которые были запущены
и последовательность переходов, которые были запущены 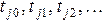 . Эти две последовательности связаны следующим соотношением:
. Эти две последовательности связаны следующим соотношением: 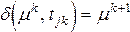 для k = 0,1,2, ... . Имея последовательность переходов и m0, легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Таким образом, обе эти последовательности представляют описание выполнения сети Петри.
для k = 0,1,2, ... . Имея последовательность переходов и m0, легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Таким образом, обе эти последовательности представляют описание выполнения сети Петри.
Пусть некоторый переход в маркировке m разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке m есть новая маркировка m'. Говорят, что m' является непосредственно достижимой из маркировки m, иными словами, состояние m' непосредственно получается из состояния m.
Определение 7. Для сети Петри С = (Р, Т, I, O) с маркировкой m маркировка m' называется непосредственно достижимой из m, если существует переход tjÎT, такой, что d(m, tj) = m'.
Можно распространить это понятие на определение множества достижимых маркировок данной маркированной сети Петри. Если m' непосредственно достижима из m, а m'' – из m', говорят, что m" достижима из m. Определим множество достижимости R(C, m) сети Петри С с маркировкой m как множество всех маркировок, достижимых из m. Маркировка m' принадлежит R(C, m), если существует какая-либо последовательность запусков переходов, изменяющих m на m'. Отношение «достижимости» является рефлексивным, транзитивным замыканием отношения «непосредственной достижимости».
Определение 8. Множество достижимости R(C, m) дли сети Петри С = = (Р, Т, I, O) с маркировкой m есть наименьшее множество маркировок, определенных следующим образом:
1. m Î R(C, m);
2. Если m' Î R(C, m) и m'' = d(m, tj) для некоторого tj Î T, то m'' Î R(C, m).
События и условия
Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События – это действия, имеющие место в системе. Возникновением событий управляет состояние системы. Состояние системы может быть описано множеством условий. Условие – есть предикат или логическое описание состояния системы. Условие может принимать либо значение «истина», либо значение «ложь».
Так как события являются действиями, то они могут происходить. Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение ; предусловий и может привести к выполнению других условий, постусловий.
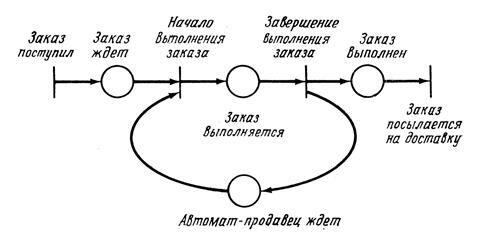
В качестве примера рассмотрим задачу моделирования простого автомата–продавца. Автомат–продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются: а) автомат–продавец ждет; б) заказ прибыл и ждет; в) автомат–продавец выполняет заказ; г) заказ выполнен. Событиями будут: 1. Заказ поступил. 2. Автомат–продавец начинает выполнение заказа. 3. Автомат–продавец заканчивает выполнение заказа. 4. Заказ посылается на доставку. Предусловия события 2 (автомат–продавец начинает выполнение заказа) очевидны: (а) автомат–продавец ждет; (б) заказ прибыл и ждет. Постусловие для события 2: (в) автомат–продавец выполняет заказ. Аналогично мы можем определить предусловия и постусловия для других событий и составить следующую таблицу событий и их пред– и постусловий:
| Событие | Предусловия | Постусловия |
| 1 | нет | б |
| 2 | а, б | в |
| 3 | в | г, а |
| 4 | г | нет |
Такое представление системы легко моделировать сетью Петри. В сети Петри условия моделируются позициями, события – переходами. При этом входы перехода являются предусловиями соответствующего события; выходы – постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий.
Сеть Петри на рис.6.6 иллюстрирует модель приведенного выше автомата–продавца.
|
Рис.5.6. Сеть Петри для простого автомата–продавца |
ЭВМ с конвейерной обработкой
Возможность моделировать параллелизм и довольно простого объединения подсистем, представленных сетями Петри, делают сети Петри весьма полезным инструментом моделирования сложной аппаратуры вычислительных систем. Вычислительные системы состоят из многих компонент. Это делает сеть Петри наиболее подходящим средством для их представления.
На протяжении ряда лет было предпринято много попыток увеличения производительности вычислительных систем путем параллельного выполнения нескольких функций. Примером такого подхода к построению высокопроизводительной ЭВМ является использование конвейерной обработки. Этот метод обработки подобен функционированию сборочного конвейера и особенно удобен для работы с векторами и массивами. Конвейер состоит из набора операций, которые могут выполняться одновременно. Когда операция k завершается, она передает свой результат операции (k + 1) и ожидает от операции (k — 1) нового задания. Если каждая операция занимает t единиц времени и всего существует n операций, то завершение обработки одного операнда потребует nt единиц времени. Однако, если на конвейерную обработку продолжают поступать новые операнды, результаты могут выдаваться со скоростью один каждые t единиц времени.
В качестве примера рассмотрим сложение двух чисел с плавающей точкой. Основные шаги этой операции предполагают:
1. Выделить экспоненты обоих чисел.
2. Сравнить экспоненты и изменить, если необходимо, должным образом порядок большей и меньшей экспонент.
3. Сдвинуть точку в числе с меньшей экспонентой для их уравнения.
4. Сложить дроби.
5. Нормализовать результат.
6. Проверить экспоненту на переполнение и сформировать экспоненту и дробь результата.
Каждый из этих шагов может быть выполнен отдельным вычислительным блоком, где каждый отдельный операнд передается от блока к блоку для выполнения операции сложения. Это позволит выполнять до шести сложений одновременно.
Координацию различных блоков можно осуществлять несколькими способами. Обычно управление конвейерной обработкой является синхронным: время, отпущенное на выполнение каждого шага конвейера t, постоянно и фиксировано. Каждые t единиц времени результат каждого блока перемещается по конвейеру, чтобы стать входом для следующего блока. Однако при синхронном подходе обработка может быть приостановлена без необходимости, так как требуемое время может изменяться от блока к блоку, а также внутри данного блока для различных входов. Например, для выполнения шага нормализации результата при сложении чисел с плавающей точкой может потребоваться различное количество времени в зависимости от того, на сколько разрядов необходимо произвести нормализующий сдвиг и в какую сторону: вправо или влево. В этом случае, поскольку время t должно быть выбрано максимальным, необходимым для самого медленного блока конвейера, может оказаться так, что большую часть времени все единицы будут пребывать незагруженными, ожидая окончания t единиц времени.
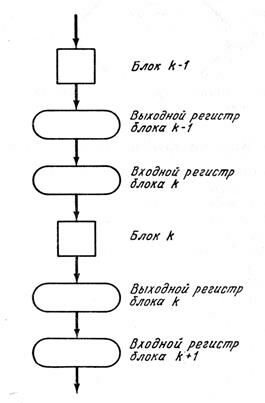
В асинхронном конвейере в среднем процесс обработки может быть ускорен сигнализацией о завершении каждого шага конвейерной обработки и готовности передать свой операнд и получить новый. Результат шага k конвейерной обработки может быть послан на шаг (k + 1), как только шаг k выполнен, а блок {k + 1) свободен. Рассмотрим произвольный шаг конвейерной обработки. Очевидно, нужно иметь место, куда можно поместить входы и выходы в то время, как они используются или производятся. Обычно это предполагает наличие регистров: блок использует значение своего входного (буферного) регистра для вычисления значения выходного (буферного) регистра. После этого необходимо ждать, пока (1) – выходной регистр блока не будет очищен путем пересылки содержимого во входной регистр следующего блока и (2) – новое входное значение не появится в его входном регистре. Таким образом, для управления блоком k конвейера необходимо знать, когда выполняются следующие условия:
· входной регистр заполнен; входной регистр пуст;
· выходной регистр заполнен; выходной регистр пуст;
· блок занят;
· блок свободен;
· пересылка осуществлена.
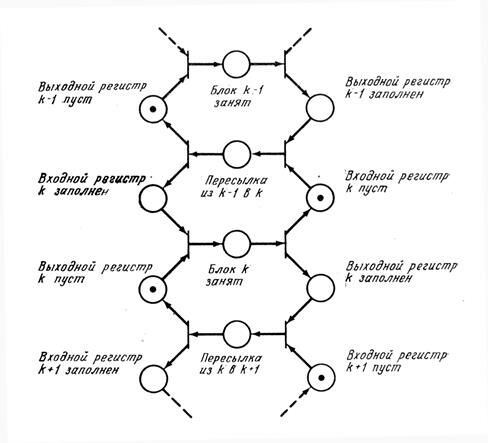
На рис.5.7 и 5.8 показано, как можно промоделировать асинхронный конвейер такого типа. На рис. 5.7 приведена блок-схема конвейера, моделируемого сетью Петри на рис. 5.8.
|
Рис.5.7 |
Отметим, что в этой модели мы промоделировали реальную работу блоков конвейера как непримитивных событий. Это позволяет нам игнорировать на этом уровне конкретные детали того, что делают блоки, и сосредоточиться на их правильном взаимодействии. Каждая операция также может быть промоделирована сетью Петри. Затем сети Петри для каждого блока можно внести в сеть Петри на рис. ???, получив более детальную сеть. Такая возможность моделирования системы на нескольких различных уровнях абстракции, т. е. иерархическим образом, может быть весьма полезна.
|
Рис.5.8. |
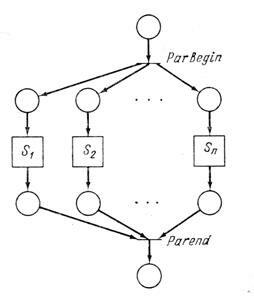
Для введения параллелизма предлагается операциях parbegin и parend (рис.6.9). Структура управления была предложена Дейкстрой и имеет вид parbegin S1; S2; ...; Sn parend, где Si – предложение. Смысл структуры parbegin/parend заключается в параллельном выполнении каждого из предложений S1, S2, ..., Sn.
|
Рис.5.9. |
Задача о взаимном исключении
Предположим, что несколько процессов разделяют общую переменную, запись, файл или другой элемент данных. Этот разделяемый элемент данных может использоваться процессами различными способами, упрощенно их можно классифицировать как чтение значения элемента данных или запись нового значения. Эти две операции являются часто единственными примитивными операциями. Это означает, что для обновления разделяемого элемента данных процесс должен сначала считать старое значение, затем вычислить новое и, наконец, записать его на то же место. Если два процесса в одно и то же время пытаются выполнить такую последовательность действий, то могут возникнуть трудности. Возможна следующая последовательность:
1. Первый процесс считывает значение х из разделяемого объекта;
2. Второй процесс считывает значение х из разделяемого объекта;
3. Первый процесс вычисляет новое значение х' = f(x);
4. Второй процесс вычисляет новое значение х" = g(x);
5. Первый процесс записывает х' в разделяемый объект;
6. Второй процесс записывает х" в разделяемый объект, уничтожая значение х'.
Результат вычисления первого процесса потерян, так как теперь значением разделяемого объекта является g(x), в то время как им должно быть либо g(f (х)), либо f(g(x)). (Представьте себе, что g(x) – «снять со счета х тысяч долл.», f(x) – «поместить на счет х тысяч долл.», а процессы 1 и 2 – банковские операции.)
Для предотвращения проблем такого рода необходимо обеспечить механизм взаимного исключения. Взаимное исключение – это метод создания таких программ, что одновременно не более чем один процесс имеет доступ к разделяемому объекту данных. Участок кода, в котором осуществляется доступ к разделяемому объекту и который требует защиты от вмешательства других процессов, называется критической секцией. Идея состоит в том, что когда процесс готов выполнить свою критическую секцию, он сначала ждет, пока другой процесс не выполнит свою собственную критическую секцию. Затем он «блокирует» доступ к критической секции, не давая возможности никакому другому процессу войти в свою критическую секцию. Он входит в критическую секцию, выполняет ее и, выйдя из нее, освобождает ее для доступа со стороны других процессов.
|
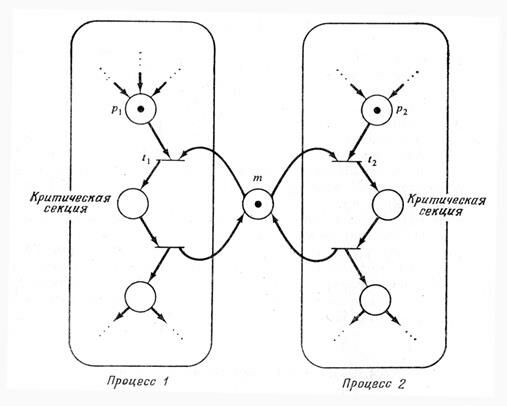
Рис.5.10. Взаимное исключение. |
Эта задача может быть решена сетью Петри, как показано на рис.6.10. Позиция m представляет собой разрешение для входа в критическую секцию. Для того чтобы какой-либо процесс вошел в критическую секцию, он должен иметь фишку в p1 или в p2 соответственно, свидетельствующую о желании попасть в критическую секцию, а также должна существовать фишка в m, дающая разрешение на вход. Если оба процесса пытаются войти в критическую секцию одновременно, то переходы t1 и t2 вступят в конфликт, и только один из них сможет запуститься. Запуск t1 запретит переход t2, вынуждая процесс 2 ждать, пока первый процесс выйдет из своей критической секции и возвратит фишку обратно в позицию m.
Задача о производителе/потребителе
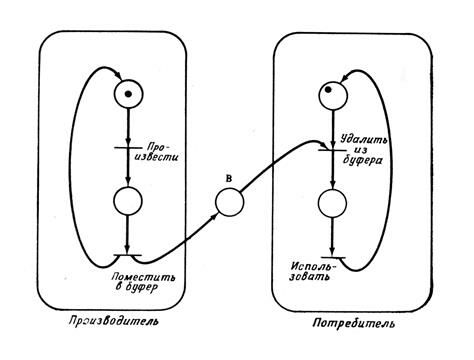
В задаче о производителе/потребителе также присутствует совместно используемый объект, но в этом случае разделяемый объект точно определен и является буфером. Процесс-производитель создает объекты, которые помещаются в буфер. Потребитель ждет, пока объект не будет помещен в буфер, удаляет его оттуда и использует. Такая ситуация может быть промоделирована сетью Петри так, как показано на рис.5.11. Позиция B представляет собой буфер, каждая фишка соответствует элементу данных, который произведен, но еще не использован.
|
Рис.5.11. Задача о производителе/потреьителе |
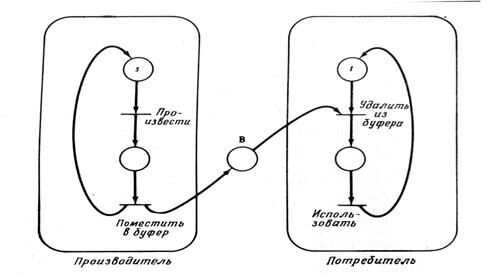
Один из вариантов этой задачи – это задача о нескольких производителях/нескольких потребителях. В этом случае несколько производителей порождают элементы данных, помещаемые в общий буфер, для нескольких потребителей. На рис.5.12 представлено решение этой задачи в виде сети Петри. Эта сеть совпадает с сетью на рис.5.11, за исключением того, что для представления s производителей и t потребителей мы начали выполнение сети с s фишками в начальной позиции процесса-производителя и t фишками в начальной позиции процесса-потребителя. Таким образом мы представляем s производителей и t потребителей, реализуемых реентерабельными совместно используемыми программами. Альтернативой было бы дублирование программного кода для процессов производителя и потребителя, однако результатом этого при том же самом поведении была бы гораздо большая сеть.
|
Рис.5.12. |
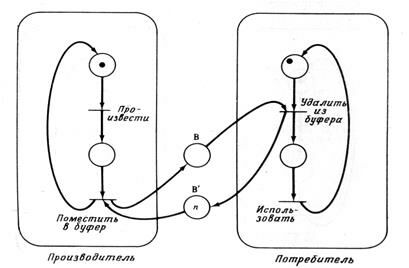
В другом варианте задачи о производителе/потребителе используется буфер ограниченного размера. При такой постановке задачи буфер между производителем и потребителем ограничен, т. е. имеет только n ячеек для элементов данных. Следовательно, производитель не может постоянно работать с той скоростью, которая ему нужна, а вынужден ждать, если потребитель работает медленно и буфер заполнен. На рис.5.13 показано решение этой проблемы. Ограниченному буферу сопоставляются две позиции: B представляет количество элементов данных, которые произведены, но еще не использованы (число заполненных ячеек). B' – количество пустых ячеек в буфере. Первоначально B' имеет n фишек, а B фишек не имеет. Если буфер заполнен, то B' фишек не имеет, а B имеет n фишек. Если теперь производитель попытается поместить еще один элемент данных в буфер, то. он будет остановлен, так как в В' нет фишки, делающей этот переход разрешенным.
|
Рис.5.13. |
Химические системы – другой пример систем, которые могут быть промоделированы сетями Петри. Химические уравнения моделируются переходами; вещества, участвующие в реакции, – позициями. Количество фишек в позиции указывает на количество данного вещества в системе. Например, сеть Петри на рис.5.14 представляет два химических уравнения:
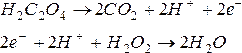
|
Рис.5.14 |
Безопасность
Одно из важнейших свойств сети Петри, которая должна моделировать реальное устройство, – безопасность. Позиция сети Петри является безопасной, если число фишек в ней никогда не превышает 1. Сеть Петри безопасна, если безопасны все позиции сети.
Определение 10. Позиция piÎP сети Петри С= (Р, Т, I, O) с начальной маркировкой m является безопасной, если m'£1 для любой m' Î R(C, m). Сеть Петри безопасна, если безопасна каждая ее позиция.
Безопасность – очень важное свойство для устройств аппаратного обеспечения. Если позиция безопасна, то число фишек в ней равно 0 или 1. Следовательно, позицию можно реализовать одним триггером.
В первоначальном определении сети Петри были безопасны, поскольку переход не мог быть запущен, если не все из выходных позиций были пусты (а кратные дуги не были разрешены). Это объяснялось интерпретацией позиции как условия. Условие, будучи логическим высказыванием, либо истинно (представляется фишкой в позиции), либо ложно (представляется отсутствием фишки); кратные фишки не имеют никакой интерпретации. Таким образом, если интерпретировать сети как условия и события, маркировка каждой позиции должна быть безопасной.
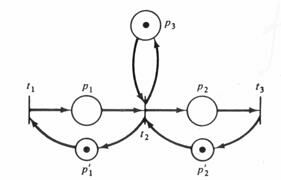
Если позиция не является кратной входной или кратной выходной для перехода, ее можно сделать безопасной. К позиции pi, которую необходимо сделать безопасной, добавляется новая позиция p'i. Переходы, в которых pi используется в качестве входной или выходной, модифицируются следующим образом:
Если piÎ I(tj) и pi Ï O(tj), тогда добавить p'i к O(tj).
Если pi Î O(tj) и pi Ï I(tj), тогда добавить p'i к I(tj).
|
Рис.5.15 Рис.5.16 |
Цель введения этой новой позиции p'i – представить условие «pi пуста». Следовательно, pi и p'i дополнительны; pi имеет фишку, только если p'i не имеет фишки и наоборот. Любой переход, удаляющий фишку из pi, должен помещать фишку в p'i, а всякий переход, удаляющий фишку из pi, должен помещать фишку в p'i. Начальная маркировка также должна быть модифицирована для обеспечения того, чтобы точно одна фишка была либо в pi, либо в p'i. (Мы допускаем, что начальная маркировка безопасна.) Заметим, что такая принудительная безопасность возможна только для позиций, которые в начальной маркировке являются безопасными и входная и выходная кратность которых равна 0 или 1 для всех переходов. Позиция, имеющая для некоторого перехода выходную кратность 2, будет получать при его запуске две фишки и, следовательно, не может быть безопасной. Простая сеть Петри на рис.5.15 реобразована в безопасную, как показано на рис.6.16
Ограниченность
Безопасность – это частный случай более общего свойства ограниченности. Некоторые соображения относительно реального ограничения на аппаратную, реализацию позиций позволяют прийти к заключению, что безопасность – необязательное требование. Безопасность позволяет реализовать позицию триггером, но в более общем случае можно использовать счетчик. Однако любой аппаратно реализованный счетчик ограничен по максимальному числу, которое он может представить. Позиция является k-безопасной или k-ограниченной, если количество фишек в ней не может превышать целое число k.
Определение 11. Позиция pi Î P сети Петри С = (Р, Т, I, O) с начальной маркировкой m является k-беэопасной, если m'(pi) £ k для всех m' Î R(C, m).
Иногда нас будет интересовать только то, является число фишек в позиции ограниченным или нет, а не конкретное значение границы. Позиция называется ограниченной, если она k–безопасна для некоторого k; сеть Петри ограниченна, если все ее позиции ограниченны. Ограниченную сеть Петри можно реализовать аппаратно, тогда как сеть Петри с неограниченными позициями в общем cлучае реализовать аппаратно нельзя.
Методы анализа
В этом разделе мы представим два основных метода анализа сетей Петри, которые описывают механизмы решения некоторых из уже перечисленных задач. Первый метод анализа, используемый для сетей Петри, – это дерево достижимости, второй метод связан с. матричными уравнениями. Обсудим каждый из них.
Дерево достижимости
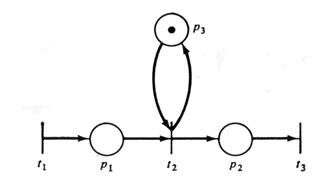
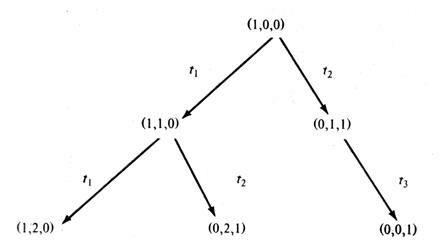
Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис.5.17. Начальная маркировка ее – (1, 0, 0). В этой начальной маркировке разрешены два перехода: t1 и t2. Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис.5.18). Это (частичное) дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.
|
Рис.5.17. |
Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1, 1, 0) можно снова запустить t1 (получая (1, 2, 0)) и t2 (получая (0, 2, 1)); из (0, 1, 1) можно запустить t3 (получая (0, 0, 1)). Это порождает дерево, изображенное на рис.5.19. Начиная с трех новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево, как показано на рис.5.20.
|
|
Рис.5.18
Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешенным, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут. Кроме того, необходимо отметить, что маркировка (0, 1,1), порождаемая запуском t3 в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском t2.
|
Рис.5.19. |
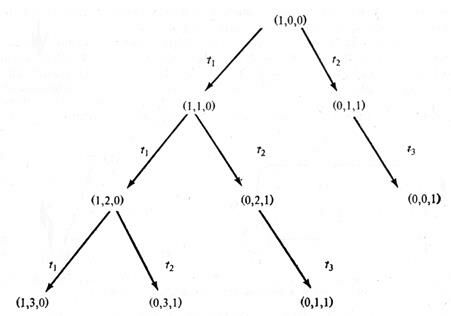
Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порожденной. Однако получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рис.5.21).
|
Рис.5.21. Простая сеть Петри с бесконечным деревом. |
Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера.
Приведение к конечному представлению осуществляется несколькими способами. Нам необходимо найти те средства, которые ограничивают введение новых маркировок (называемых граничными вершинами) на каждом шаге. Здесь могут помочь пассивные маркировки – маркировки, в которых нет разрешенных переходов. Эти пассивные маркировки называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Такие дублирующие маркировки называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве.
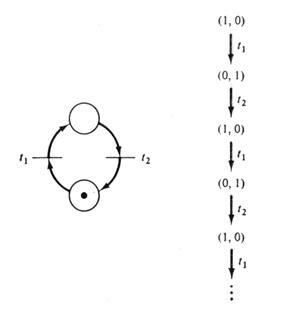
В сети Петри на рис.5.16, например, можно запустить переход t1 столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в p2.
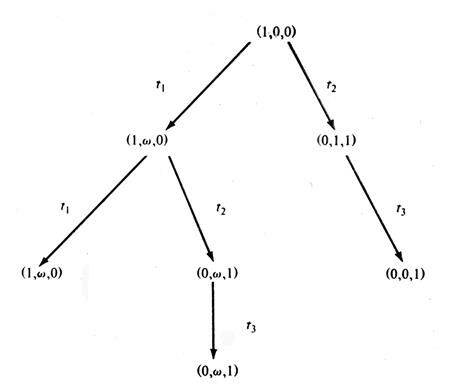
Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа w, который обозначает «бесконечность». Для любого постоянного a определим
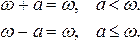
Для построения дерева достижимости необходимы только эти операции над w.
Теперь можно точно сформулировать действительный алгоритм построения дерева достижимости. Каждая вершина i дерева связывается с расширенной маркировкой m[i]; в расширенной маркировке число фишек в позиции может быть либо неотрицательным целым, либо w. Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые еще не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.
|
Рис.5.22. |
Алгоритм начинает работу с определения начальной маркировки корнем дерева, т. е. граничной вершиной. До тех пор пока имеются граничные вершины, они обрабатываются алгоритмом.
Пусть х – граничная вершина, которую необходимо обработать.
1. Если в дереве имеется другая вершина у, не являющаяся граничной, и с ней связана та же маркировка, m[х] = m[y], то вершина х – дублирующая.
2. Если для маркировки m[х] ни один из переходов не разрешен (т. е. d(m[x], tj) не определено для всех tj Î T), то х – терминальная вершина.
3. Для всякого перехода tj Î T, разрешенного в m[х] (т. е. d(m[х], tj) определено), создать новую вершину z дерева достижимости. Маркировка m[z], связанная с этой вершиной, определяется для каждой позиции pi следующим образом:
В лекции "6 - Пневмомоторы" также много полезной информации.
а) Если .m[x]i = w, то m[z]i = w.
б) Если на пути от корневой вершины к х существует вершина у с m[y] < d(mlxl, tj) и m[y]i < d(m[x], tj)i, то m[z]i = w.
в) В противном случае m[z]i = d(m[х], tj)i.
Дуга, помеченная tj, направлена от вершины х к вершине z. Вершина х переопределяется как внутренняя, вершина z становится граничной.
Когда все вершины дерева – терминальные, дублирующие или внутренние, алгоритм останавливается.
На рис.5.22 представлено дерево достижимости для сети Петри на рис.5.16.