Анализ запаздывания

Тема 8. Анализ запаздывания

 Основные понятия и определения

Любому реальному объекту присуща инерция, прояв­ляющаяся в том, что изменение его состояния сопро­вождается переходным процессом.

 Качественные особенности свойств экономиче­ского объекта, которые могут трактоваться как инерцион­ные, приводят к необходимости их статистиче­ской оценки путем обработки информации о наблюдае­мых траекториях входов и выходов объектов.

Наблюдаемым эффектом «инерции» является запазды­вание выхода или состояние элемента относи­тельно момента изменения входного воздействия. Так, например, «запаздывает» выпуск готовой продукции отно­сительно момента выделения для этой цели капиталь­ных вложений.

Рассмотрим некоторые линейные модели запаздыва­ния, которыми обычно пользуются при анализе функционирования экономических объектов.

 В таких моделях выходная переменная может быть представлена в виде суперпозиции ее «идеального» значе­ния (безынерционный элемент) и составляющей, поро­ждаемой инерцией объекта (Рис 5.1.). Поэтому при анализе запаздывания и его влияние на поведение эле­мента удобно различать потенциальное и запаздывающие значения выходной переменной:

1. y⁰(t) = C_j x(t) – для идеального выхода.

Рекомендуемые материалы

2. y(t) – для выхода с запаздыванием.

Схема интерпретирующая взаимодействие обоих вы­ходов.

Рисунок 5.1.

где F⁰ – «идеальный» преобразователь;

      U – инерционное звено, моделирующее запаздыва­ние.

Внутреннее состояние этого звена g_u(t) определя­ется накопленным в нем запасом вещества, энергии или информации.

Существует две оценки запаздывания и его влияние на поведение объекта.

Первая характеристика это длительность запаздыва­ния (временной лаг) обозначается - Т.  Она достаточна для описания установившегося режима функ­ционирования объекта, при котором Y, Y⁰ и g_u  сохра­няют постоянное значение, а Y=Y⁰. Временной лаг мо­жет быть регламентирован (например, длительность транс­портировки продукта, время информационного сооб­щения) или определен путем наблюдений. То есть в установившемся режиме

                                            (5.1).

Вторая характеристика -форма связи между потенци­альными и запаздывающими выходами в переход­ном режиме. Ее выбор осуществляется на основе качественного анализа наблюдаемого переходного про­цесса, логических соображений, оценки возможности полу­чения необходимой информации.

Типовые непрерывные модели запаздывания

Простейшей является запаздывание в форме 

                  (5.2),        

которая предполагает, что запаздывающий выход ко­пирует потенциальный с лагом , исчисляемым в непре­рывной шкале задержки   
        

                        (5.3).

Зависимость (5.3) приемлема для описания запаздыва­ния во многих объектах хранения и транспорти­ровки продукции. Чаще всего модель запаздыва­ния строится в предположении, что скорость изменения запаздывающего выхода, определяется величи­ной его отставания от потенциального выхода то есть,

                         (5.4).

Такая гипотеза достаточно хорошо согласуется с на­блюдаемым поведением экономических объектов и логи­кой переходных режимов в инерционных элементах.

 Коэффициент λ в зависимости (5.4) соответствует ско­рости изменения переменной Y(t) при отставании запаз­дывающего выхода относительно потенциального, равном единице. Его называют скоростью реакции.

Описываемая модель может быть представлена в сле­дующей эквивалентной форме.

               (5.5),

где f(θ) = λу^--λθ – весовая функция, значения кото­рой характеризуют влияние предшествующих входных воздействий на текущую величину запаздывающего вы­хода (эффект наследственности), причем:

          .

Запаздывание в форме (5.4) или (5.5) называются по­казательным (экспоненциальным).

Предположим, что потенциальный выход представ­ляет собой ступенчатую функцию, где выполняются сле­дующие условия:

                        Y⁰(t) = 0; t≤0,

                        Y⁰(t) = Y⁰; t≥0                   (5.6),

порождаемую скачкообразным изменением интенсив­ности входной переменной X(t). Тогда уравне­ние (5.4) записывается в следующей форме:

                       ,

а его решение при начальном условии Y(0)=0 имеет сле­дующий вид:

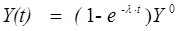
Рисунок 5.2.

Время Т, по истечению которого разность Y(t) - Y⁰(t) не превосходит некоторые величины ε, определя­ется соотношением  и должно соответство­вать регламентированному или наблюдаемому лагу. Из этого соотношения определяем величину λ. Если при­нять, что, то при отклонение
ε =Y⁰/ε ≈ 0,379Y⁰. Площадь, заключенная между прямой линией Y⁰(t) и кривой α (Рис.5.2) определяет состояние инерционного звена.

Показательное запаздывание достаточно хорошо опи­сывает переходные режимы, присущие многим реаль­ным экономическим процессам. Таковы, например, измене­ние потребительского спроса на товар, вызванный снижением его цены, процесс освоения капитальных вложе­ний на строительство объекта и так далее. Однако для моделирования запаздывания, например, в спросе на новый товар, порождаемого психологической инерцией потребителей, эта форма не проходит. Здесь более прием­лема кривая δ. Она может быть получена с помо­щью модели, образованной двумя последовательно соеди­ненными инерционными звеньями типа зависимо­сти (5.4). Это запаздывание второго порядка описывается системой из двух дифференциальных уравнений, реше­ние которых дает кривую δ.

Для некоторых переходных режимов подходящая ап­проксимация запаздывания достигается с помощью пока­зательных моделей третьего и более высоких поряд­ков. С ростом порядка увеличивается начальная фаза кри­вой запаздывания и крутизна ее восходящей ветви, что дает более удовлетворенное приближение к реаль­ным процессам, имеющим такой характер.

Дискретные модели запаздывания

Пусть θ и τ - номера временных интервалов, а контро­лируемые моменты времени отнесены к их кон­цам. Дискретная модель запаздывания описывается соотно­шением (2), в котором время t и лаг  целочис­лены:

                        (5.7)

В частном, но в распределенном случае  прини­мают равной единице (годовой производственный цикл) и .

Вместе с тем зависимость (5.7) сама является част­ным случаем распределенного запаздывания, при кото­ром предполагается, что запаздывающий выход зависит  от совокупности  прошлых значений потенциальной пере­менной, взятых с убывающими весами β_θ. Тогда

Рекомендация для Вас - Функции сетевого уровня.

Принимая в зависимости (5.8) веса убывающими по геометрической прогрессии со знаменателем  r (1>r>0), получим модель, являющуюся дискретным аналогом показа­тельного запаздывания первого порядка:

               (5.9)

Соответствующее этой форме конечно-разностное уравнение имеет вид:

             ,                                                               (10)

где λ=1-r,  а  Y_τ+1 = Y_τ + ΔY_τ   τ = 1, 2, ....