Анализ экономической системы
Тема 7. Анализ экономической системы
Методические вопросы анализа. Идентификация объекта
Под идентификацией объекта обычно понимают определение его характеристик и приложенных к нему воздействий. В статистических задачах вероятностные характеристики внешних воздействий получаются путем обработки наблюдений. С помощью статистических методов также находят и характеристики объекта.
Экономический объект, подлежащий идентификации, чаще всего представляется перед исследователем как "черный ящик", обозреваемый со стороны его входов и выходов. Его идентификация реализуется с помощью экономико-статистической модели, описывающей зависимости между входными и выходными переменными. Будем полагать, что выходы взаимонезависимы, тогда задача идентификации объекта с n - выходами сводится к идентификации n - одновыходных "черных ящиков".
Построение экономико-статистической модели включает два последовательных этапа:
1. Выбор формы связи между переменными, выраженной в виде уравнения регрессии выходной переменной Y на входные переменные Хs (S=1,…, m)
2. Оценивание параметров регрессии.
Для первого этапа определяющее значение имеет качественный анализ процесса, реализуемого объектом. Чаще всего для целей моделирования используют полиномы и степенные функции.
Рекомендуемые материалы
Для второго этапа основным вопросом является выбор способа оценивания, обеспечивающего необходимые свойства получаемых оценок (состоятельность, несмещенность, эффективность).
Наиболее распространенным является метод наименьших квадратов (МНК). Оценки, получаемые этим методом, будут несмещенными, оптимальными, если соблюдаются следующие условия:
1. Переменные Хs контролируемые (то есть неслучайны), взаимонезависимы;
2. Отклонение ε, наблюдаемых значений переменных от линии регрессии являются статистически независимыми, случайными величинами со средним равным нулю и конечной дисперсией;
3. Переменные Xs не коррелированны с возмущением ε.
Статистические данные о входных и выходных переменных могут быть получены путем одномоментных наблюдений над множеством однотипных объектов или по временным рядам, получаемым в результате наблюдения траектории входов и выходов объекта.
При изучении экономических объектов чаще всего приходится прибегать ко второму способу формирования статистической информации.
В силу самих свойств системы как совокупности взаимодействующих объектов между их состояниями существуют статистические связи, характер которых зависит от структуры системы. Естественно попытаться оценить их с помощью моделей охватывающих два множества переменных:
1. g1(t) ,…, gk (t);
2. X1(t),…, Xm (t)
и формируемой в виде системы уравнений связей:
 (4.1)
(4.1)
где Fj – функции, выбранные на основе теоретических предпосылок, качественного анализа и других соображений;
С0, С1, ..., Cτ – параметры, оцениваемые по наблюдениям;
ε j – ненаблюдаемые случайные возмущения.
Такая модель может рассматриваться как стохастическое обобщение детерминированной экономико-математической модели (где ε j = 0).
Аппроксимация статистической зависимости
Пусть в результате наблюдений множество однородных объектов, получено n – пар значений (Xi, Yj ) входной и выходной переменных. Анализ показывает, что Х и Y являются величинами случайными и можно предположить наличие стохастической связи между ними. Примем переменную Х за аргумент, а Y за функцию.
Предположим, что в исходной совокупности стохастическая зависимость между указанными переменными описывается уравнением регрессии Е (у) = F(x), где:
Е (у) –математическое ожидание у, вид и параметры которой нам неизвестны. Но мы располагаем упомянутой выборкой из n пар значений аргумента и случайной функции Y(x). Задачей идентификации является:
1. выбрать функцию Y=F(x,C), аппроксимирующую функцию f(x), заданную выборочной таблицей;
2. определить ее параметры и оценить на этой основе параметры регрессии Y на X генеральной совокупности.
Предположим, что Хτ и Yτ - интенсивности входа и выхода изучаемого объекта, наблюдаемые в фиксированные моменты времени (τ = 1,…, n). Ряды Хτ и Yτ являются реализациями случайных нестационарных процессов. Поэтому при формировании зависимости:
Y (t) = F[x(t), C] (4.2)
необходимо учитывать особенности временных рядов, порождаемых этими процессами.
В общем случае наблюдаемые значения Yτ формируются в результате естественного переплетения следующих компонентов ряда:
1. регулярный компонент ỹ=ỹτ характеризующий общую тенденцию изменения во времени изучаемого показателя. Его называют тенденцией или трендом ряда;
2. периодический компонент со средним значением, равным нулю. Он образуется как совокупность наложенных друг на друга колебаний с различными периодами;
3. чисто случайных компонент, значения ετ которого не коррелированны. Обычно предполагают, что они не зависят от указанных выше компонентов.
Задача анализа временного ряда сводится к его преобразованию, обеспечивающему выделение (фильтрацию) того или иного компонента, определяемого целью исследования, и к оценке его параметров. Выделяемый компонент рассматривается при этом, как полезная составляющая ряда, а остальные как помехи.
Таким образом, речь идет о выборе преобразователя, называемого в данном случае фильтром, на вход которого поступает временная последовательность Yτ .Его выходом является предписанная функция полезной составляющей ряда.
Пусть исследуемый ряд является реакцией дискретного аддитивного случайного процесса, образованного суммой двух независимых составляющих: регулярный Ỹτ, с математическим ожиданием, зависящим от времени, и стационарной случайной помехи ετ с математическим ожиданием равным нулю:
Yτ = Ỹτ + ετ (4.3)
Составляющую Ỹτ будем считать тенденцией.
Нашей задачей является оценка ее параметров в исходном процессе (4.3) по выборке из n-пар значений Yτ и τ, доставляемой наблюдаемым рядом.
Эта процедура осуществляется с помощью линейного преобразователя, на вход которого поступает последовательность Yτ. Его выходом должна быть предписанная функция Y-непрерывная, аппроксимирующая составляющую Ỹτ (τ = 1,…, n).
Указанное преобразование обычно называют сглаживанием ряда, а математическую модель - сглаживающим фильтром.
В качестве аппроксимирующей функции чаще всего выбирают полиномы и экспоненты с постоянными параметрами:
 (4.4)
(4.4)
 (4.5)
(4.5)
В некоторых случаях выделение компонента может быть осуществлено путем авторегрессивного преобразования наблюдаемого ряда. Текущее значение контролируемого показателя зависит от его значения в предшествующие моменты времени, а его изменение за наблюдаемое время близко к стационарному. Тогда для модели процесса можно принять функцию:
 (4.6)
(4.6)
в которой параметры βӨ подлежат оценке.
Оценка надежности регулярной составляющей, полученной путем обработки временного ряда, основывается только на изучении внутренней структуры его остаточных членов έτ. Можно рекомендовать следующую процедуру такой оценки:
1. Отфильтруем тенденцию и переходим к анализу отклонений от нее на основании ряда
ετ = yτ – Yτ. (4.7)
2. Если анализ процесса не дает оснований предполагать в нем наличие колебаний, то принимают гипотезу, что остатки (4.7) не коррелированы. Обычно ограничиваются автокорреляцией первого порядка и, если она незначительно отличается от нуля, то гипотеза не отклоняется. Следовательно, модель может быть описана соотношением Yτ = уτ + ετ , где ετ - случайные помехи взаимно независимы.
Предположим, что:
 ;
;
 ,
,
где εхτ и εуτ - стационарные случайные отклонения.
Для построения аппроксимирующей функции F и оценки ее параметров можно применить два способа.
При первом способе из обоих рядов исключаются тенденции и затем решается задача оценки параметров регрессии У на Х, оперируя с отклонениями εх и εу как рядами независимых случайных величин.
Второй способ базируется на теореме Фриша и Воу, согласно которой регрессия, построенная по отклонениям от линейных тенденций, эквивалентна прямому включению времени как дополнительного фактора в уравнение регрессии для самих переменных.
Нахождение параметров эмпирической
зависимости методом наименьших квадратов
Бывают случаи, когда сама измеряемая величина за время измерений меняется вследствие непостоянства другой величины, связанной с ней. В этих случаях будет наблюдаться статистический разброс, приводящий к случайным погрешностям. Этот разброс будет происходить не относительно неизменного "истинного" значения или среднего значения измеряемой величины, а относительно изменяющегося «истинного» значения.
Пусть в результате эксперимента мы получили ряд изменений величины Y: у1, у2,...,уn, соответствующих значениям аргумента t1,t2, ...,tn, которые могут быть представлены на графике в виде точек. Необходимо установить эмпирическую зависимость между Y и t.
Очевидно, если соединить последовательно все эти точки, то получим ломаную линию, которая ничего общего не будет иметь с искомой зависимостью Y=f(t). Форма этой ломаной линии не будет воспроизводиться при повторных сериях измерений. Измеренные значения Yi будут в общем случае смещены относительно искомой кривой Y=f(t) как в сторону больших, так и в сторону меньших значений, вследствие статистического разброса.
Задача состоит в том, чтобы по данным экспериментальным точкам провести кривую, которая проходила бы как можно ближе к истинной функциональной зависимости Y = f(t).
Теория вероятностей показывает, что наилучшим приближением будет такая кривая линия, для которой сумма квадратов расстояний по вертикали от точек до кривой будет минимальной. Этот метод называется методом наименьших квадратов.
Предположим, что искомая зависимость выражается функцией Y = f(t, a1, ..., am), где аi – параметры. Значения этих параметров определяются так, чтобы точки уi располагались по обе стороны кривой у = f(x) как можно ближе к последней, то есть чтобы сумма квадратов отклонений измеренных уi от функции Y=f(t) была бы наименьшей. Разброс точек Yi относительно кривой Y=f(t) подчиняется закону нормального распределения. Мерой этого разброса является дисперсия σ2 или ее приблизительное выражение - средний квадрат отклонения.
 (4.8)
(4.8)
Функция f(а) принимает минимальные значения при а = аmin, если ее первая производная  , а ее вторая производная
, а ее вторая производная  . При этом значение а = аmin. Для функций многих переменных эти условия заменяются требованием, чтобы частные производные, то есть. производные по параметру аi удовлетворяли вышеупомянутым условиям, причем все остальные параметры ai (j≠i) при вычислении произвольных считаются постоянными.
. При этом значение а = аmin. Для функций многих переменных эти условия заменяются требованием, чтобы частные производные, то есть. производные по параметру аi удовлетворяли вышеупомянутым условиям, причем все остальные параметры ai (j≠i) при вычислении произвольных считаются постоянными.
Таким образом, из условий минимума получаем систему уравнений для определения наилучших значений параметра:
 (i=1,…,m;m<n) (4.9)
(i=1,…,m;m<n) (4.9)
Обычно форму зависимости у=f(t, a1, ..., an) задают в виде полинома
 (m<n-1) (4.10)
(m<n-1) (4.10)
или в виде любой другой системы линейно-независимых функций φk(t):
 (4.11)
(4.11)
достаточно хорошо передающей общий ход зависимости y=f(t). В случае выбора f(t) в виде (4.10) уравнение (4.9) примет следующий вид:

В случае выбора разложения функция в форме (4.11) уравнение (4.9) примет следующий вид:

Решение этих систем линейных уравнений позволяет однозначно определить коэффициенты аi разложения Y=f(t). Изложенный выше способ применения метода наименьших квадратов можно обобщить и на некоторые случаи нелинейных зависимостей f(t, A) например:
Y = f(t, α, γ) = α e -γ t (4.14)
В этом случае целесообразно искать минимум суммы квадратов отклонений логарифмов этих же функций:
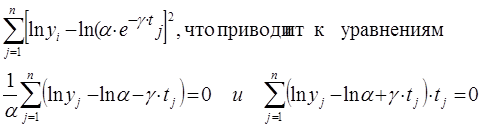
то есть к системе уравнений
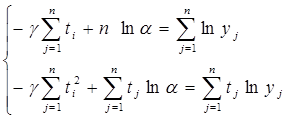
Решение которой дает значение параметров γ и ln α

Нахождение параметров линейной зависимости Y(t)=d+bt
Рассмотрим нахождение параметров линейной зависимости на следующим примере.
Пример №1. При изменении электрического сопротивления R проволоки при разной температуре tc (из семи серий измерений) получены следующие результаты:
Таблица 4.1
| I | ti,c | Ri,Ом | tiRi | ti2 | R(ti ) вычисленное | ∆Ri |
| 1 | 20.0 | 86.70 | 1734 | 400 | 86.65 | +0.05 |
| 2 | 24.8 | 88.03 | 2183 | 615 | 88.21 | -0.18 |
| 3 | 30.2 | 90.32 | 2728 | 912 | 89.97 | +0.35 |
| 4 | 35.0 | 91.15 | 3190 | 1225 | 91.53 | -0.38 |
| 5 | 40.1 | 93.26 | 3740 | 1608 | 93.18 | +0.08 |
| 6 | 44.9 | 94.90 | 4261 | 2016 | 94.74 | +0.16 |
| 7 | 50.0 | 96.33 | 4816 | 2500 | 96.40 | -0.07 |
| Сумма | 245.0 | 640.69 | 22652 | 9276 | +0.01 | |
| среднее | 35.0 | 91.527 | 3236 | 1325 |
Найдем температурную зависимость сопротивления проволоки R=R0+at, используя метод наименьших квадратов.
1. Потребуем, чтобы сумма квадратов отклонений была наименьшей.
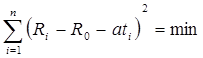
Из этого условия, дифференцируя его сначала по R0, а затем по a получаем уравнения:

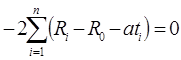
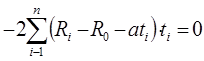
 далее раскрывая скобки получаем:
далее раскрывая скобки получаем:
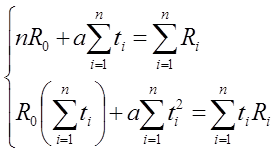
Из первого уравнения выразим R0:
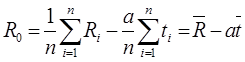
и подставляя это выражение во второе уравнение получим:
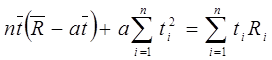
из него определим значение a
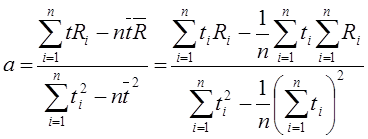
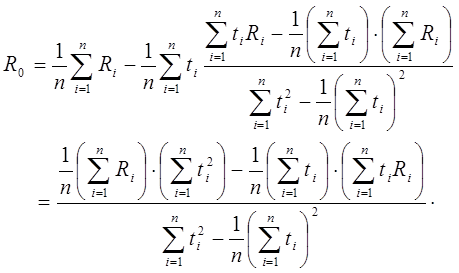
Подставляя в формулы численные значения получаем:
Обратите внимание на лекцию "5.8. Обзор рынка программных продуктов".
 Ом/град
Ом/град
 Ом
Ом
Таким образом, мы получаем
 Ом.
Ом.
Проведенный сравнительный анализ результатов измерения и результатов полученных по данной линейной зависимости показал (Таблица 4.1), что отклонение незначительно и составляет 0.01 в сумме по всем сериям.























