Лекция 11.

План:

1. Принцип Гюйгенса-Френеля;

2. Зоны Френеля.

§4.11.1. Принцип Гюйгенса-Френеля

Проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса. Однако этот принцип не дает сведений об амплитуде, а следовательно и об интенсивности волн, распространяю­щихся в различных направлениях. Френель дополнил принцип Гюйгенса представле­нием об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн по­зволяет найти амплитуду результирующей волны в любой точке пространства. Разви­тый таким способом принцип Гюйгенса получил название принципа  Гюйгенса—Френеля.

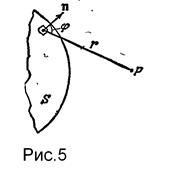
Согласно принципу Гюйгенса—Френе­ля каждый элемент волновой поверхности  (рис. 5) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента.

Амплитуда сферической волны убывает с расстоянием  от источника по закону . Следовательно, от каждого участка  волновой поверхности в точку, лежащую перед этой поверхностью, приходит колебание

                                                (4.13)

В этом выражении  — фаза колебания в месте расположе­ния волновой поверхности , — волновое число, — расстояние от элемента поверхности  до точки . Множитель  определяется амплитудой светового колебания в том месте, где находится . Коэффициент , зависит от угла  между нормалью  к площадке  и направлением от  к точке . При  этот коэффициент мак­симален, при  он обращается в нуль.

Рекомендуемые материалы

Результирующее колебание в точке  представляет собой супер­позицию колебаний (4.13), взятых для всей волновой поверхности :

                                          (4.14)

Эта формула является аналитическим выражением принципа Гюйгенса — Френеля.

§4.11.2. Зоны Френеля

Вычисления по формуле (4.14) представляют собой в общем случае очень трудную задачу. Однако, как показал Френель, в случаях отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическими или геометрическим суммированием.

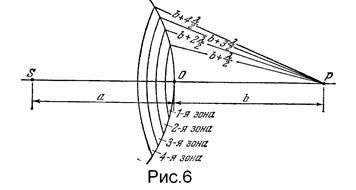
Чтобы понять суть метода, разработанного Френелем, определим амплитуду светового колебания, возбуждаемого в точке  сфериче­ской волной, распространяющейся в изотропной однородной среде из точечного источника  (рис.6). Волновые поверхности такой волны симметричны относительно прямой . Воспользовавшись этим, разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки  отличаются на  ( — длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны носят название зон Френеля.

Из (рис.6) видно, что расстояние  от внешнего края -й зоны до точки  равно

,                                                     (4.15)

где — расстояние от вершины волновой поверхности  до точки .

Колебания, приходящие в точку  от аналогичных точек двух соседних зон (т. е. от точек, лежащих в середине зон, или у внешних краев зон и т. д.), находятся в противофазе. Поэтому и результирую­щие колебания, создаваемые каждой из зон в целом, будут для со­седних зон отличаться по фазе на .

Вычислим площади зон. Внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты  (рис.7). Обозначим площадь этого сегмента через . Тогда площадь m-й зоны можно представить в виде

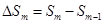
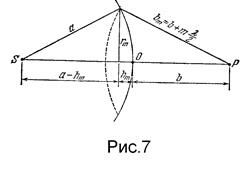
Из (рис.7) видно, что

,

где — радиус волновой поверхности, — радиус внешней границы m-й зоны.

Отсюда

                                                 (4.16)

Ограничившись рассмотрением не слишком больших , можно ввиду малости  пренебречь слагаемым, содержащим . В этом прибли­жении

                                                    (4.17)

Площадь сферического сегмента равна  (—радиус сферы, —высота сегмента). Следовательно,

,

а площадь m–й зоны

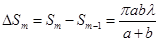
Полученное нами выражение не зависит от . Это означает, что при не слишком больших  площади зон Френеля примерно одинаковы.

Расстояние  от зоны до точки медленно растет с номером зоны . Угол  между нормалью к элементам зоны и направлением на точку  также растет с . Все это приводит к тому, что амплитуда колебания, возбуждаемого от m-й зоной в точке , монотонно убывает с ростом . Даже при очень больших m, когда площадь зоны начи­нает заметно расти с , убывание множителя  перевешивает рост , так что  продолжает убывать. Таким образом, амплитуды колебаний, возбуждаемых в точке  зонами Френеля, образуют монотонно убывающую последовательность:

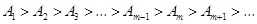
Фазы колебаний, возбуждаемых соседними зонами, отличаются на . Поэтому амплитуда  результирующего колебания в точке  может быть представлена в виде

                                               (4.18)

В это выражение все амплитуды от нечетных зов входят с одним зна­ком, а от четных зон — с другим. Запишем выражение (4.18) в виде

Ещё посмотрите лекцию "Воспалительные заболевания селезенки" по этой теме.

                          (4.19)

Вследствие монотонного убывания  можно приближенно считать, что

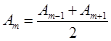
Тогда выражения в скобках будут равны нулю, и формула (4.19) упрощается следующим образом:

.                                                          (4.20)

Согласно формуле (4.20) амплитуда, создаваемая в некоторой точке  всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. Если на пути волны поставить непрозрачный экран с отверстием, оставляю­щим открытой только центральную зону Френеля, амплитуда в точке  будет равна , т. е. в два раза превзойдет амплитуду (4.20). Соответственно интенсивность света в точке  будет в этом случае в четыре раза больше, чем при отсутствии преград между точками  и .