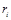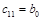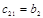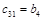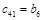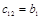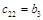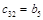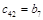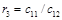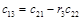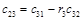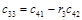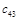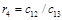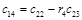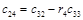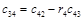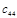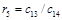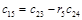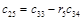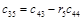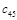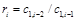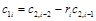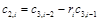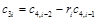Критерии устойчивости Гурвица и Рауса
Критерии устойчивости Гурвица и Рауса (алгебраические)
Необходимое и достаточное условие устойчивости системы управления без решения характеристического уравнения было сформулировано Гурвицем в виде неравенств [3]. Пусть характеристическое уравнение системы управления имеет вид:
bo sn+ b1 sn-1+ ... + bn = 0.
Тогда с учетом его коэффициентов может быть составлена матрица Гурвица:
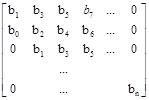
При составлении матрицы Гурвица по диагонали записываются коэффициенты характеристического уравнения, начиная с b1. Строки вправо от диагонали заполняются коэффициентами в порядке возрастания индексов, а слева – в порядке убывания. Несуществующие коэффициенты ассоциируются с нулем. Гурвиц доказал, что для выполнения условия устойчивости, то есть для расположения всех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы при bo > 0 все определители Гурвица (определители диагональных миноров матрицы Гурвица)
 1 = b1 > 0;
1 = b1 > 0;  2 =
2 =  > 0; ...
> 0; ...
были положительными. Остановимся кратко на некоторых общих замечаниях. Вычисление определителей Гурвица высоких порядков непосредственным разложением их по элементам строки или столбца сопряжено с большим числом вычислений и неоправданной затратой времени, поэтому весьма полезны правила, упрощающие расчеты:
1) для расположения всех корней характеристического уравнения слева от
мнимой оси необходимо (но недостаточно), чтобы все коэффициенты bi
Рекомендуемые материалы
были одного знака;
2) обращение в нуль определителя  i свидетельствует о появлении пары
i свидетельствует о появлении пары
чисто мнимых корней;
3) если все коэффициенты характеристического уравнения положительны, то
все вещественные корни (если они есть) отрицательны. Комплексные
корни при этом могут лежать и в правой полуплоскости;
4) если в последовательности b0, b1, b2,…, bn имеется одна перемена знака, то
имеется один корень, лежащий в правой полуплоскости. Если число
перемен знака равно N > 1, то число таких корней равно N;
5) критерий Гурвица удобно применять для уравнений не выше четвертой
степени. Для более высоких степеней целесообразнее использовать
алгоритм Рауса, ориентированный на использование ЭВМ в расчетах.
Критерий Рауса состоит в следующем [4]. Положим, что найдена передаточная функция замкнутой автоматической системы в форме
 .
.
Характеристическое уравнение при этом имеет вид:
 = 0.
= 0.
Составим таблицу, которая называется таблицей Рауса
Таблица 2.
| Коэфф. | i | Столбец | ||||
| 1 | 2 | 3 | 4 | |||
| - | 1 |
|
|
|
| |
| - | 2 |
|
|
|
| |
|
| 3 |
|
|
|
| |
|
| 4 |
|
|
|
| |
|
| 5 |
|
|
|
| |
| … | . | … | … | … | … | |
|
| i |
|
|
|
| |
| … | ... | … | … | 20. Проблемы внутрибольничных инфекций - лекция, которая пользуется популярностью у тех, кто читал эту лекцию. … | … |
Алгоритм составления матрицы Рауса очевиден. Сформулируем критерий устойчивости. Для того чтобы автоматическая система была устойчива необходимо и достаточно, чтобы выполнялись условия:

 .
.
Если хотя бы один коэффициент характеристического уравнения отрицателен, то система неустойчива, а если равен нулю, то это свидетельствует о появлении пары чисто мнимых корней, что характерно для неустойчивых систем управления, либо находящихся на границе устойчивости. Число отрицательных коэффициентов равно числу правых полюсов. В таблице Рауса для упрощения расчетов элементы строк можно делить или умножать на положительные величины. Таблица, реализующая алгоритм Рауса, удобна для программирования на ЭВМ, поэтому с помощью этого метода можно исследовать на устойчивость системы высокого порядка, а также исследовать влияние на устойчивость отдельных параметров системы.