Частотные характеристики дискретных систем

ЛЕКЦИЯ №8

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИСТЕМ.

План лекции:

1. Определение изображения гармонического сигнала.

2. Прохождение дискретного гармонического сигнала через импульсную систему.

3. Частотные характеристики импульсных систем.

4. Свойства частотных характеристик импульсных систем.

8.1. Прохождение дискретного гармонического сигнала через импульсную систему.

Рекомендуемые материалы

Определим реакцию импульсной системы с ПФ W(z)  на гармонический сигнал

.

При решении данной задачи удобно рассмотреть реакцию системы на воздействие:

              (8.1)

и далее выделить действительную часть найденной реакции?

Найдем изображение сигнала (8.1). Преобразование по Лапласу функции:

.

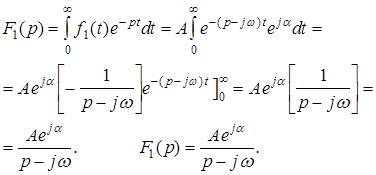
Таким образом: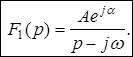                      

С использованием теории вычетов:

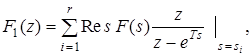
получим:

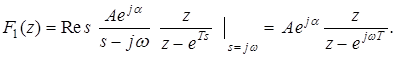
Изображение выходной переменной системы имеет вид:

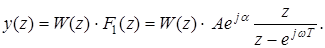
Для получения реакции импульсной системы на заданный сигнал (8.1), выполним обратное Z- преобразование от последнего уравнения:

             (8.2)

Использована формула:

, где z_i - полюсы Z-изображения.

В выражении (8.2) вычеты берутся в полюсах ПФ W(z)  и в точке z=e^jwT. Положим для простоты, что полюсы z₁, z₂,...z_r  передаточной функции простые и удовлетворяют условию:

                               (8.3)

Тогда:

                                                (8.4)

При выполнении условия (8.3) второе слагаемое в правой части (8.4) стремится к 0 при n®бесконечности и в системе устанавливается вынужденное движение:

              (8.5)

Выделяя в выражении (8.5) действительную часть, получим реакцию системы на входной гармонический сигнал:

              (8.6)

Из полученной зависимости (8.6) видно, что при прохождении гармонического сигнала через импульсную систему его амплитуда изменяется в

  - раз, а фаза изменяется на   .

8.2 Частотные характеристики импульсных систем.

Функция W^*(jw) = W(e^jwT),  получающаяся из Z-ПФ  W(z) в результате подстановки z=e^jwT, называется амплитудно-фазовой частотной характеристикой импульсной системы.

Функция A^*(w) = êW(e^jwT)ê, называется амплитудно частотной характеристикой (АЧХ), а  функция j^*(w)=argW(e^jwT) – фазо-частотная характеристика (ФЧХ) импульсной системы.

Частотные характеристики импульсной системы имеют тот же смысл, что и соответствующие характеристики непрерывных систем и позволяют найти установившуюся реакцию на гармоническое воздействие.

Определение АФЧХ импульсной системы возможно с помощью формул:

                                    (8.7)

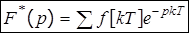
либо с использованием формулы связи:

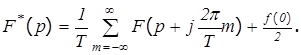
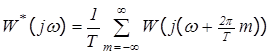
Пример

Рассмотрим пример определения АФЧХ импульсной системы. Пусть Z=ПФ системы имеет вид:

.

Необходимо найти ЧХ звена.

Решение:

В соответствии с определением ЧХ, имеем:

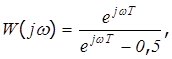
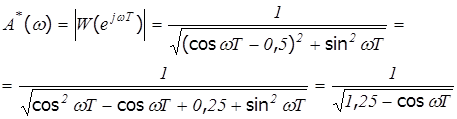
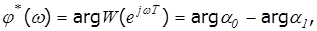
где: a₀- аргумент числителя;

a₁- аргумент числителя.

a₀ =wT;

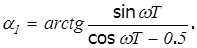
Графики АФЧХ, построенные по приведенным зависимостям, показаны на рис.8.1, здесь =wТ.

Из приведенного рисунка видно, что частотные характеристики импульсных систем существенно отличаются от АФЧХ непрерывных систем.

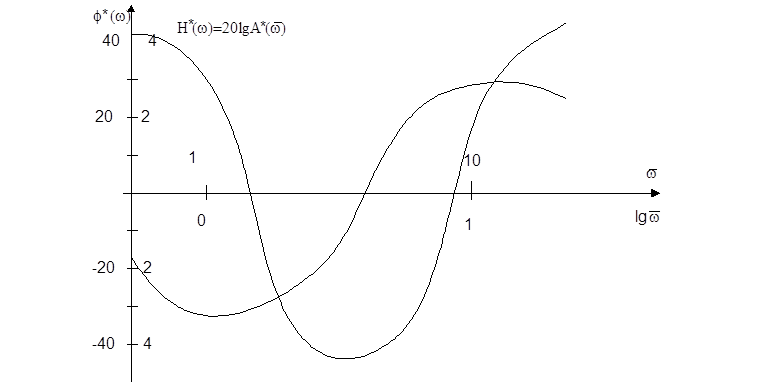
Рис.8.1.

8.3. Свойства частотных характеристик импульсных систем.

Рассмотрим основные свойства ЧХ импульсных систем.

1. В общем случае ЧХ импульсных систем являются функциями параметра e:

W(e^jwT,e).

.

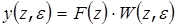
Таким образом, импульсная система, строго говоря описывается семейством ЧХ. Тем не менее, при исследовании свойств импульсных систем достаточно ограничиться случаем e=0. Например, при оценке устойчивости используется именно ЧХ W(e^jwT).

2.Вследствие периодичности экспоненты e^jwT ЧХ импульсной системы является периодической функцией частоты с периодом: .

e^jwT=

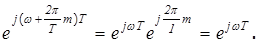
Поэтому ЧХ W(e^jwT)  полностью определяется своими значениями в диапазоне частот:

.

Периодичность ЧХ приводит к тому, что импульсная система одинаково пропускает сигналы  sin wt и sin (wt+), так как в обоих случаях на выходе ИИЭ существуют одинаковые последовательности импульсов (рис.8.2).

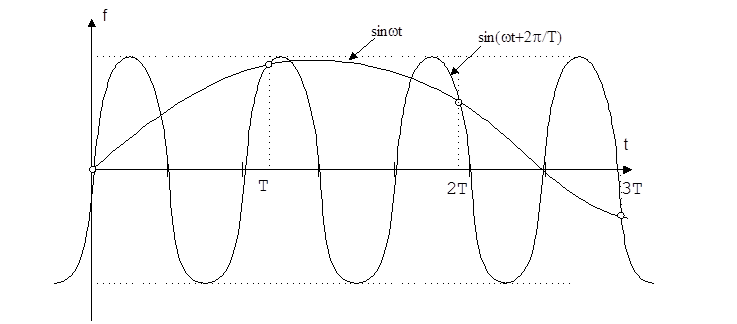
Рис.8.2.

Допустим частота входного сигнала в 5 раз меньше частоты квантования:

.

Далее рассмотрим входной сигнал, частота которого отличается от указанной на величину   :

+=6*.

3. АЧХ  A^*(w,e) является четной функцией частоты, т.е. :

A^*(w,e) = A^*( - w,e).

Вследствие четности АЧХ и периодичности W(e^jwT, e) достаточно знать значения АЧХ в диапазоне

.

Фзочастотная характеристика j^* (w,e) является нечетной функцией частоты, т.е.:

j^* (w,e) = - j^* ( - w,e).

Она также может быть задана своими значениями в диапазоне частот:

.

4. При частотах , где ,  n  = 0,±1,...., т.е.

,   n =0,±1,...

или

j^*() = pn, n =0,±1,...

Указанное свойство выполняется за исключением случаев, когда передаточная функция  приведенной непрерывной части W(p) имеет нулевой полюс порядка l. Тогда ПФ W(z) имеет полюс  z=1 того же порядка l. И при w®0, А^*(w,e)® к бесконечности, j^*(w,e)®.

5. При рассмотрении непрерывных систем широко использовались логарифмические  частотные характеристики. Их преимущество заключалось в возможности аппроксимации ломаными линиями, что позволяло использовать так называемые асимптотические  частотные характеристики.

Вам также может быть полезна лекция "7.2 - Примеры применения уравнения Бернулли".

Использование логарифмического масштаба для частотных характеристик  дискретных систем не дает хороших результатов.

Возможный вид АЧХ дискретной системы в логарифмическом масштабе  приведен на рис.8.3.

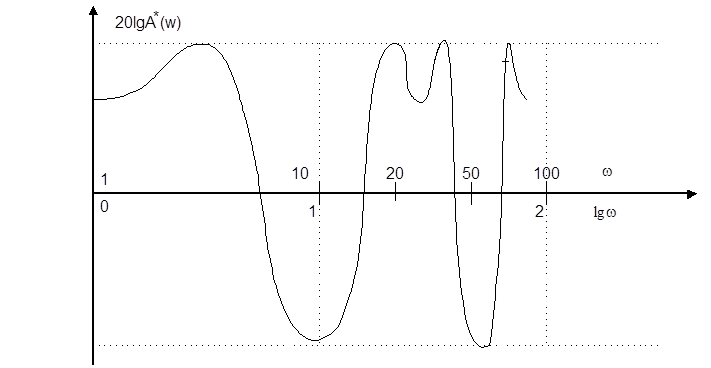
Рис.8.3.

Вследствие того, что W^*(jw) -  периодическая функция частоты, логарифмические частотные характеристики  дискретных систем  теряют свойства асимптотичности  и не могут быть аппроксимированы ломаными линиями.

Таким образом, в своем исходном виде, ЧХ дискретных систем неудобны для применения и нуждаются в определенной модификации, чтобы их можно было применить  также просто, как  и ЛАФЧХ непрерывных систем.