💯Высшая математика Темы 7-12 / Самый полный сборник из 229 правильных ответов на отлично! 100/100
Описание
Введение
Тема 7. Предел функции
Тема 8. Дифференциальное исчисление функции одной переменной
Тема 9. Интегральное исчисление функции одной переменной
Тема 10. Функции нескольких переменных
Тема 11. Обыкновенные дифференциальные уравнения порядка
Тема 12. Линейные дифференциальные уравнения высших порядков
Заключение
Итоговая аттестация
Абсциссами точек перегиба графика функции y = x³ / 6 − x² / 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
3
4
Абсциссами точек перегиба графика функции y = x³ являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2
3
0
4
Боковые стороны и меньшее основание трапеции равны по 10 см. Определить ее большее основание так, чтобы площадь трапеции была наибольшей.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
13 см
15 см
22 см
20 см
25 см
Вертикальными асимптотами графика функции y = lnx являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
х = е
х = 0
х = 1
х = –1
∅
Выберите правильный ответ на вопрос: производная [c ⋅ u(x) - d ⋅ v(x)]'], гдеси d —действительныечисла, равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
c' ⋅ u(x) − d' ⋅ v(x)
c ⋅ u'(x) + d ⋅ v'(x)
c ⋅ u'(x) − d ⋅ v'(x)
c ⋅ u'(x) − d ⋅ v(x)
0
Выберите правильный ответ на вопрос: производная [u(x) ⋅ v(x)]' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
u'(x) ⋅ v(x)
u(x) ⋅ v'(x)
u'(x) ⋅ v'(x)
u'(x) + v'(x)
u'(x)v(x) + u(x)v'(x)
Выберите правильный ответ на вопрос. Производная функции [u(x) / c]', где с — действительное число, равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
u'(x) / c'
cu'(x)
−u'(x) / c
u'(x) / c
u'(x) / c²
Вычислить ∫ √(4 − 5x)dx, x=−12..−1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
54 2/3
18 1/3
64 2/3
15
10
Вычислить ∫ dx / (a² + x²), x=a..a√3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
π / 2a
π / 3a
π / 12a
π / 4a
π / 6a
Вычислить ∫ dx / (x² + 6x + 8), x=2..8
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2 ⋅ ln(5/4)
ln(5/4)
3/4 ⋅ ln(5/4)
3 ⋅ ln(5/4)
2ln3
Вычислить ∫ dx / √(x² + 1), x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 + √2
ln2 + 1
2 ⋅ ln│1 + √2│
3 ⋅ ln│1 + √2│
ln│1 + √2│
Вычислить ∫ e^(x/3)dx, x=0..3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
е –1
2(e + 1)
2(e - 1)
3(e - 1)
1/2 ⋅ (e - 1)
Вычислить ∫ sin2xdx, x=0..π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
0
2
3/2
1/2
Вычислить ∫ sin4xdx, x=0..π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
1/3
2
1/2
Вычислить ∫ x³dx, x=1..3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
10
15
-20
-10
20
Вычислить ∫ xe^(x²)dx, x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
е –1
2е –1
3е +1
(e + 1) / 2
(e − 1) / 2
Вычислить ∫ xeˣdx, x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
2
1
3
4
Вычислить приближенно приращение функции y = x² + 2x + 3 когда х изменяется от 2 до 1,98.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,3
–0,5
0,01
–0,12
0,05
Геометрически первая производная от функции, если она существует, есть
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Синус угла наклона касательной к оси ОХ
Косинус угла наклона касательной к оси ОХ
Тангенс угла наклона касательной к оси ОХ
Котангенс угла наклона касательной к оси ОХ
Дифференциал функции y = sin²2x равен
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 sin 2 xdx
2 cos2 xdx
–2 sin 2 xdx
sin 4 xdx
2 sin 4 xdx
Дифференциал функции y = x³ + 3x² + 3x равен
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(6x⁴ + 3x³ + 3x³)dx
(3x² + 6x + 3)dx
(3x² + 6x)dx
(x⁴ / 4 + x³ + 3 ⋅ x² / 2)dx
(x⁴ + 3x + 3)dx
Достаточными условиями существования производной непрерывной функции в точке являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Существование хотя бы одной односторонней производной
Существование двух односторонних производных
Существование и равенство двух односторонних производных
Заменив приращение функции дифференциалом, приближенно найти arctg 1,05.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,75
0,69
0,81
0,80
0,65
Заменив приращение функции дифференциалом, приближенно найти sin 31°.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,500
0,451
0,35
0,515
0,491
Из непрерывности функции
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
следует ее дифференцируемость
еще не следует ее дифференцируемость
следует разрывность первой производной
следует непрерывность первой производной
Какая из заданных функций задана явно:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ху = 5;
x² + y² = 9;
у = sinx;
eˣʸ = 3;
lg(x + y) = 5.
Какая из заданных функций является обратной для функции Y=5x-3:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x = (y − 3) / 5;
x = (y + 3) / 5;
x = (5y − 3) / 5;
x = (3y − 5) / 5;
x = (3y + 5) / 5.
Какая из заданных функций является четной:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
y = x² - x;
y = x⁴ - 2x²;
y = x⁴ - x²;
y = x + 2;
y = x.
Касательная к графику функции y = x² в точке M₀(1; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 1
у = 2х – 1
у = 2х + 1
у = х –1
у = 2х + 3
Наибольшим значением функции y = x² − 2x на отрезке [–1; 1] является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1
3
5
∞
10
Найдите вторую производную заданной функции y = x / (x − 1)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
−1 / (x − 1)²
−1 / (x − 1)³
1 / (x − 1)⁴
2 / (x − 1)³
−2 / (x − 1)³
Найдите вторую производную функции у = sin2x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 sin 2x
4 cos 2x
– 4sin 2x
4 sin 2x
cos 2x
Найти все точки разрыва функции y = (2x - 1) / (x² - 8x + 15)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2
2 и 6
1 и 2
3 и 5
1 и 4
Найти интеграл ∫ ((√x - 1)² / x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x√x − 2√x + ln|x| + c
x − 4√x + ln|x| + c
√x − 4x + ln|x| + c
√x − 2√x + ln|x| + c
x + 2√x + ln|x| + c
Найти интеграл ∫ ((10x⁵ + 5) / x³ )dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
10x³ + x² + c
10x² + x + c
10 / 3 ⋅ x³ - 5 / (2x²) + c
10 / 3 ⋅ x² - 5 / (2x) + c
10 / 3 ⋅ x - 5 / (2x) + c
Найти интеграл ∫ (√x + ∛x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x√x + x∛x + c
2/3 ⋅ x√x − 3/4 ⋅ x∛x + c
2 ⋅ x√x + 3 ⋅ x∛x + c
3/2 ⋅ x√x + 4/3 ⋅ x∛x + c
2/3 ⋅ x√x + 3/4 ⋅ x∛x + c
Найти интеграл ∫ (2 / (1 + x²) − 3 / √(1 − x²))dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 ⋅ arctgx − 3 ⋅ arcsinx + c
1/2 ⋅ arctgx + arcsinx + c
2 ⋅ arctgx − arccosx + c
2 ⋅ arcsinx − 3 ⋅ arctgx + c
2 ⋅ arccosx + 3 ⋅ arctgx + c
Найти интеграл ∫ (4 − 3x)e⁻²ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / 4 ⋅ e⁻²ˣ + C
(2x − 3) / 4 ⋅ e⁻²ˣ + C
3xe⁻²ˣ + C
(5 − 6x) / 4 ⋅ e⁻²ˣ + C
(6x − 5) / 4 ⋅ e⁻²ˣ + C
Найти интеграл ∫ ⁵√(x³)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/5 ⋅ x ⋅ ⁵√(x³) + c
5/8 ⋅ x ⋅ ⁵√(x³) + c
3/5 ⋅ x^(3/5) + c
−5/2 ⋅ x^(−2/5) + c
5/8 ⋅ x² ⋅ ⁵√(x³) + c
Найти интеграл ∫ aˣ(1 + a⁻ˣ / √(x³))dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
aˣ / lna − 3/2 ⋅ √x + c
aˣ / lna + 3/2 ⋅ √x + c
aˣ / lna − 3/2 ⋅ ∛x + c
aˣ / lna − 2/2 ⋅ ∛x + c
aˣ / lna + 3/2 ⋅ ∛x + c
Найти интеграл ∫ cos2xdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1/2 ⋅ sin2x + C
1/2 ⋅ sinx + C
cos²2x / 2 + C
1/2 ⋅ sin2x + C
sin2x + C
Найти интеграл ∫ dx / (√x + 1)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ln│√x + 1│+ C
1/2 ⋅ ln│√x + 1│+ C
√x + 2ln│√x + 1│+ C
2√x − 2ln│√x + 1│+ C
2√x + 2ln│√x + 1│+ C
Найти интеграл ∫ cos²xdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
cos³x / 3 + c
1/2 ⋅ x + 1/4 ⋅ sin2x + c
1/2 ⋅ cos³x + c
x + sin2x + c
1/2 ⋅ x - 1/4 ⋅ sin2x + c
Найти интеграл ∫ dx / (x² + 6x + 13)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
arcsin(x + 3) + c
arcsin((x + 3) / 2) + c
arctg(x + 3) + c
1/2 ⋅ arctg((x + 3) / 2) + c
2arctg(x + 3) + c
Найти интеграл ∫ dx / √(4 − x²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
arcsinx + c
arccosx + c
arcsin(x/2) + c
arctg(x/2) + c
1/2 ⋅ arctg(x/2) + c
Найти интеграл ∫ dx / √(x² + 3x)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2 ⋅ √(x² + 3x) + C
ln│x + 3/2 + √(x² + 3x)│+ C
2 ⋅ √(x² + 3x) + C
3 ⋅ ln│x + √(x² + 3x)│
ln│x + √(x² + 3x)│
Найти интеграл ∫ e⁵⁻³ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(5 - 3x)e⁵⁻³ˣ + C
−1/3 ⋅ e⁵⁻³ˣ + C
e⁵⁻³ˣ + C
1/3 ⋅ e⁵⁻³ˣ + C
e⁵⁻³ˣ ⋅ ln|5 − 3x| + C
Найти интеграл ∫ eˣdx / (e²ˣ − a²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / (2a) ⋅ ln│(eˣ − a) / (eˣ + a)│+ C
e²ˣ − a² + C
1 / a ⋅ (e²ˣ − a²)│+ C
1 / a ⋅ ln│e²ˣ − a²│+ C
1 / (2a) ⋅ ln│e²ˣ − a²│+ C
Найтиинтеграл ∫ x√(3 − 5x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(5x + 2)√(3 - 5x) + C
(5x - 3)√(3 - 5x) + C
2/125 ⋅ (5x + 2)(5x - 3)√(3 - 5x) + C
(5x + 2)(5x - 3)√(3 - 5x) + C
(5x + 2)(5x + 3)√(3 - 5x) + C
Найти интеграл ∫ x²e⁻ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(x² + 2x + 2)e⁻ˣ + C
−(x² + 2x + 2)e⁻ˣ + C
(x² + 2)e⁻ˣ + C
(x² + 2x)e⁻ˣ + C
(x² − 2x + 2)e⁻ˣ + C
Найти интеграл ∫ x³dx / (x⁴ + 5)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ln(x⁴ + 5) + c
4 ⋅ ln(x⁴ + 5) + c
1/4 ⋅ ln(x⁴ + 5) + c
−ln(x⁴ + 5) + c
−1/4 ⋅ ln(x⁴ + 5) + c
Найти интеграл ∫ xe⁻²ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / 4 ⋅ e⁻²ˣ + C
−(2x +1) / 4 ⋅ e⁻²ˣ + C
(x +1) / 2 ⋅ e⁻²ˣ + C
(2x +1) / 4 ⋅ e⁻²ˣ + C
− x / 4 ⋅ e⁻²ˣ + C
Найти интервалы монотонного возрастания функции y = 6x² - 3x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(−∞; 1/4);
(0; 1/4);
(−∞; 3)
(1/4; +∞);
(2; +∞).
Найти интервалы монотонного убывания функции y = x³ − 3x²
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(–2; 2);
(1; 2);
(–1; 1);
(0; 2);
(0; 3).
Найти объём тела, полученного от вращения плоской фигуры, ограниченной линиями y = sinx; x = π/2, y = 0 вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
π² (куб. ед.);
π 2/4 (куб. ед.);
π (куб. ед.);
3/4 π² (куб. ед.);
2π (куб. ед.).
Найти площадь плоской фигуры, ограниченной линиями у = sinx, у = cosx, x = 0; x = π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
√2 (кв.ед.);
√2/2 (кв.ед.);
(√2 − 1) (кв.ед.);
3 (кв.ед.);
2 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями x = y² и у = –х + 2.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
4,5 (кв.ед.);
2,5 (кв.ед.);
3 (кв.ед.);
2 (кв.ед.);
3,5 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = √(lnx), y = 0, x = e вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2π (куб. ед.);
3π (куб. ед.);
π (куб. ед.);
4π (куб. ед.);
5π (куб. ед.).
Найти площадь плоской фигуры, ограниченной линиями y = lnx, y = 0, x = e вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2
3
e
5
Найти площадь плоской фигуры, ограниченной линиями y = x² - 2x + 1 у = 1.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3
4/3 (кв.ед.);
1/3 (кв.ед.);
5 (кв.ед.);
5/3 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = x² - 4x + 5; y = 5.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
8 2/3
10 2/3 (кв.ед.);
7 1/3 (кв.ед.);
10;
7 2/3(кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = x² - 9, у = 0.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
–36 кв.ед.;
18 кв.ед.;
54 кв.ед.;
36 кв.ед.;
26 кв.ед.
Найти предел на основании свойств пределов lim (4x³ − 2x² + 5x − 1), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
26
33
18
Найти предел функции lim (3x² - 5x + 2), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
2
4
22
1
Найти предел функции lim 2^(1 / (x − 1)), x⟶1−0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
2
1
−∞
Найти предел lim (√(1 + x) − 1) / sin3x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
1/6
2
Найти предел lim (1 + 5 / x)²ˣ, x⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
eˣ
e¹⁰
Найти предел lim (1 + x)^(2/x), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
e²
e⁻²
Найти предел lim (1 − cos5x) / x², x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2.5
12.5
Найти предел lim (2x² / (3 + x²) + 5^(1 / x)), x⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
5
5/3
3/5
Найти предел lim (3n − 2) / ∛(n³− 5n² + 1), n⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
2
3
1
Найти предел lim (3x² + 4x - 3) / (6x² + 5x + 7), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
1/2
2
5
Найти предел lim (3x³ + 4x² + 5) / (x⁴ − 3x + 2), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
1
2
Найти предел lim (4x - 7) / (5 - 2x), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
-2
-1
2
Найти предел lim (4x² - x + 7) / (3x + 1), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1;
2
3
Найти предел lim (eªˣ − eᵇˣ) / sinx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
а + b
∞
−∞
а – b
1
Найти предел lim (eˣ − 1) / (√(1 + x) − 1), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2
3
Найти предел lim (x − 5) / (2 − √(x − 1)), x⟶5
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
4
-4
1/2
Найти предел lim (x² - 9) / (√(x + 1) - 2), x⟶3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
24
18
Найти предел lim (x⁴ - 1) / (x³ - 1), x⟶1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
3/4
4/3
2
Найти предел lim arctgx / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
2
1
Найти предел lim ln(1 + x) / arcsinx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
1/2
2
Найти предел lim sin10x / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
10
∞
5
Найти предел lim sin2x / arcsin3x, x⟶0 @
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2/3
3
Найти предел lim sin²x / x², x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2
10
Найти предел lim tg³x / x³, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
3
2
Найти предел lim tg5x / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
5
3
Найти предел lim x / arctgx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
1
2
Найти предел, пользуясь правилом Лопиталя: lim (eˣ − 1) / (sin2x), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
-∞
2
0.5
Найти предел, пользуясь правилом Лопиталя: lim x / lnx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
-∞
1
0
-1
Найти предел: lim (1 − tgx) / cos2x, x⟶π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
-1
1
∞
5
Найти предел: lim lnx / (1 − x²), x⟶1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3
2
−1/3
1/3
∞
Найти производную y'ₓ от функции, заданной параметрически {x = atcost; y = atsint, где t ∈ [0; 2π]
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(asint + tcost) / (acost + tsint)
(sint - tcostt) / (cost + tsintt)
(sint + atcost) / (cost − atcost)
(sint + tcostt) / (cost − tsintt)
(sint + tcost) / (cost − tsint)²
Найтипроизводную y'ₓ отфункции, заданнойпараметрически {x = t², y = 4t при t = 1, где t ∈ [−∞; +∞]
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
1,1
2,2
Найти третий дифференциал функции y = 3x² - 5x + 2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3dx³
6xdx³
2dx³
0
dx³
Наклонной асимптотой графика функции y = x³ / (x² − 3) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = 0
у = 3х
у = х
у =2х
∅
Нормаль к графику функции y = eˣ в точке M₀(0; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 1
у = 2х – 1
у = 2х
у = –х + 1
у = х – 1
Нормаль к графику функции y = x² в точке M₀(1; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 2
у = х – 2
y = −1/2 ⋅ x − 3/2
y = −1/2 ⋅ x + 3/2
y = 1/2 ⋅ x − 3/2
Областью определения функции у = arc sin x является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x ∈ (−∞; +∞);
x ∈ [0; +∞);
x ∈ [−1; 1];
x ∈ (−1; 1);
x ∈ [0; 1].
Областью определения функции y = (5 − x) / √(x² − 8x + 7) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x ∈ (−∞; +∞);
x ∈ (1; 7);
x ∈ [1; 7);
x ∈ (−∞; 1) ⋃ (7; +∞);
x ∈ (−∞; 1] ⋃ [7; +∞).
Последовательность {−1/n} имеет своим пределом
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
1
2
10
Производная (x / 3)' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x² / 9
1/3
−x / 9
x / 3
−1/3
Производная (x² / 2)' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2х
х
−x² / 4
x / 2
Производная функции у = arcsin3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / √(1 − x²)
3 / √(1 − 9x²)
1 / √(1 − 9x²)
3x / √(1 − 9x²)
x / √(1 − 9x²)
Производная функции у = sin 2x при x = π/2 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
-1
-2
2
Производная функции у = tg 3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3 sec² 3x
−3 sec² 3x
3 tg * secx
−3 tg * secx
3 ctg 3x
Производная функции у(х) = с равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
с
1
0
х
сх
Производная функции у(х) = х равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
х
x²
1
2х
Производная функции eʸ + x = y равна:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / (1 + eʸ)
x / (1 − eʸ)
1 / (1 − eʸ)
y / (1 + eʸ)
xy / (1 + eʸ)
Производная функции y = 3x² − 5x + 2 при х = 1 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
-1
6
5
Производная функции y = 5³ˣ равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
5³ˣ
3x ⋅ 5³ˣ⁻¹
3 ⋅ 5³ˣln5
5³ˣln5
3 ⋅ 5³ˣ
Производная функции y = eˣ / (x + 1) равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
eˣ
−eˣ / (x + 1)²
−e / (x + 1)²
+eˣ / (x + 1)²
xeˣ / (x + 1)²
Производная функции y = log₅(3x² − 5) равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / (3x² − 5)
1 / (3x² − 5)ln5
3x² − 5
6x / (3x² − 5)ln5
6x / (3x² − 5)
Производная функции y = sin 3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
–3cos 3x
cos 3x
3sin 3x
3cos 3x
–3sin 3x
Производная функции y = x / (eˣ + 1) при х = 0 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
1/2
3
-1
Производная функции y = xeˣ при х = 0 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
3
1
0
-1
Разложить число 10 на два слагаемых, так чтобы произведение было их наибольшим.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3; 7
6; 4
1; 9
5; 5
2; 8
Решеткой длиной 120 м нужно огородить прилегающую к дому площадку наибольшей площади. Определить размеры прямоугольной площадки.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
20 м; 80 м
40 м; 40 м
30 м; 60 м
25 м; 70 м
35 м; 50 м
Сколько однозначных функций задано уравнением y² = x
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
3
4
Сравнить бесконечно малую α и β = α³ Бесконечно малая β по сравнению с бесконечно малой α является :
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
одного порядка;
второго порядка;
третьего порядка;
бесконечно большой;
эквивалентной.
Стационарными точками функции x³ / 3 - 11 / 2 ⋅ x² + 30x + 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2,3
5,6
1,3
0,2
4,8
Стационарными точками функции y = e^(x² - 2x) являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
3
4
1
-1
Стационарными точками функции y = x³ / 3 - 3x² + 5x - 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,1
1,5
2,3
1,2
3,4
Точками разрыва заданной функции y = (2x - 1) / (x² - 8x + 15) являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2
1, 2
2, 4
3, 5
0, 2
Точками разрыва заданной функции y = x / 4 + 4 / x являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2, 3
4
5
0
Точками разрыва функции y = 2^(1/x) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
1
−∞
0
2
Точками разрыва функции y = 3 / (√(x + 2) - 2) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
4
7
Точками разрыва функции y = 5 / (sinx − 1/2) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2πk;
πk;
(−1)ᵏ ⋅ π/6 + πk;
π/2 + πk;
(−1)ᵏ ⋅ π/4 + πk.
Функция y = (x - 1) / (x² - 5x + 7) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Функция y = 4x⁵ - 3x + 2 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Функция y = 7x² - 5√x - 2 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Частным значение функции y = x² + 2 при х = 3 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1
11
0
-3
-5
Частным значением функции y = {x при x ≤ 0; x² + 3 при x > 0 при х = 3 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
5
12
0
4Показать/скрыть дополнительное описание
Абсциссами точек перегиба графика функции y = x³ / 6 − x² / 2 являются: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 0 1 2 3 4 Абсциссами точек перегиба графика функции y = x³ являются: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 1 2 3 0 4 Боковые стороны и меньшее основание трапеции равны по 10 см. Определить ее большее основание так, чтобы площадь трапеции была наибольшей. Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 13 см 15 см 22 см 20 см 25 см Вертикальными асимптотами графика функции y = lnx являются: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов х = е х = 0 х = 1 х = –1 ∅ Выберите правильный ответ на вопрос: производная [c ⋅ u(x) - d ⋅ v(x)]'], где с и d — действительные числа, равна Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов c' ⋅ u(x) − d' ⋅ v(x) c ⋅ u'(x) + d ⋅ v'(x) c ⋅ u'(x) − d ⋅ v'(x) c ⋅ u'(x) − d ⋅ v(x) 0 Выберите правильный ответ на вопрос: производная [u(x) ⋅ v(x)]' равна Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов u'(x) ⋅ v(x) u(x) ⋅ v'(x) u'(x) ⋅ v'(x) u'(x) + v'(x) u'(x)v(x) + u(x)v'(x) Выберите правильный ответ на вопрос.
Производная функции [u(x) / c]', где с — действительное число, равна Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов u'(x) / c' cu'(x) −u'(x) / c u'(x) / c u'(x) / c² Вычислить ∫ √(4 − 5x)dx, x=−12..−1 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 54 2/3 18 1/3 64 2/3 15 10 Вычислить ∫ dx / (a² + x²), x=a..a√3 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов π / 2a π / 3a π / 12a π / 4a π / 6a Вычислить ∫ dx / (x² + 6x + 8), x=2..8 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 1/2 ⋅ ln(5/4) ln(5/4) 3/4 ⋅ ln(5/4) 3 ⋅ ln(5/4) 2ln3 Вычислить ∫ dx / √(x² + 1), x=0..1 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 1 + √2 ln2 + 1 2 ⋅ ln│1 + √2│ 3 ⋅ ln│1 + √2│ ln│1 + √2│ Вычислить ∫ e^(x/3)dx, x=0..3 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов е –1 2(e + 1) 2(e - 1) 3(e - 1) 1/2 ⋅ (e - 1) Вычислить ∫ sin2xdx, x=0..π/4 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 1 0 2 3/2 1/2 Вычислить ∫ sin4xdx, x=0..π/4 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 0 1 1/3 2 1/2 Вычислить ∫ x³dx, x=1..3 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 10 15 -20 -10 20 Вычислить ∫ xe^(x²)dx, x=0..1 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов е –1 2е –1 3е +1 (e + 1) / 2 (e − 1) / 2 Вычислить ∫ xeˣdx, x=0..1 Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 0 2 1 3 4 Вычислить приближенно приращение функции y = x² + 2x + 3 когда х изменяется от 2 до 1,98.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 0,3 –0,5 0,01 –0,12 0,05 Геометрически первая производная от функции, если она существует, есть Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов Синус угла наклона касательной к оси ОХ Косинус угла наклона касательной к оси ОХ Тангенс угла наклона касательной к оси ОХ Котангенс угла наклона касательной к оси ОХ Дифференциал функции y = sin²2x равен Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 2 sin 2 xdx 2 cos2 xdx –2 sin 2 xdx sin 4 xdx 2 sin 4 xdx Дифференциал функции y = x³ + 3x² + 3x равен Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов (6x⁴ + 3x³ + 3x³)dx (3x² + 6x + 3)dx (3x² + 6x)dx (x⁴ / 4 + x³ + 3 ⋅ x² / 2)dx (x⁴ + 3x + 3)dx Достаточными условиями существования производной непрерывной функции в точке являются: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов Существование хотя бы одной односторонней производной Существование двух односторонних производных Существование и равенство двух односторонних производных Заменив приращение функции дифференциалом, приближенно найти arctg 1,05.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 0,75 0,69 0,81 0,80 0,65 Заменив приращение функции дифференциалом, приближенно найти sin 31°. Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 0,500 0,451 0,35 0,515 0,491 Из непрерывности функции Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов следует ее дифференцируемость еще не следует ее дифференцируемость следует разрывность первой производной следует непрерывность первой производной Какая из заданных функций задана явно: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов ху = 5; x² + y² = 9; у = sinx; eˣʸ = 3; lg(x + y) = 5.
Какая из заданных функций является обратной для функции Y=5x-3: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов x = (y − 3) / 5; x = (y + 3) / 5; x = (5y − 3) / 5; x = (3y − 5) / 5; x = (3y + 5) / 5. Какая из заданных функций является четной: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов y = x² - x; y = x⁴ - 2x²; y = x⁴ - x²; y = x + 2; y = x. Касательная к графику функции y = x² в точке M₀(1; 1) определяется уравнением Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов у = х + 1 у = 2х – 1 у = 2х + 1 у = х –1 у = 2х + 3 Наибольшим значением функции y = x² − 2x на отрезке [–1; 1] является: Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов -1 3 5 ∞ 10 Найдите вторую производную заданной функции y = x / (x − 1) Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов −1 / (x − 1)² −1 / (x − 1)³ 1 / (x − 1)⁴ 2 / (x − 1)³ −2 / (x − 1)³ Найдите вторую производную функции у = sin2x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 2 sin 2x 4 cos 2x – 4sin 2x 4 sin 2x cos 2x Найти все точки разрыва функции y = (2x - 1) / (x² - 8x + 15) Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 1/2 2 и 6 1 и 2 3 и 5 1 и 4 Найти интеграл ∫ ((√x - 1)² / x)dx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов x√x − 2√x + ln|x| + c x − 4√x + ln|x| + c √x − 4x + ln|x| + c √x − 2√x + ln|x| + c x + 2√x + ln|x| + c Найти интеграл ∫ ((10x⁵ + 5) / x³ )dx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 10x³ + x² + c 10x² + x + c 10 / 3 ⋅ x³ - 5 / (2x²) + c 10 / 3 ⋅ x² - 5 / (2x) + c 10 / 3 ⋅ x - 5 / (2x) + c Найти интеграл ∫ (√x + ∛x)dx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов x√x + x∛x + c 2/3 ⋅ x√x − 3/4 ⋅ x∛x + c 2 ⋅ x√x + 3 ⋅ x∛x + c 3/2 ⋅ x√x + 4/3 ⋅ x∛x + c 2/3 ⋅ x√x + 3/4 ⋅ x∛x + c Найти интеграл ∫ (2 / (1 + x²) − 3 / √(1 − x²))dx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 2 ⋅ arctgx − 3 ⋅ arcsinx + c 1/2 ⋅ arctgx + arcsinx + c 2 ⋅ arctgx − arccosx + c 2 ⋅ arcsinx − 3 ⋅ arctgx + c 2 ⋅ arccosx + 3 ⋅ arctgx + c Найти интеграл ∫ (4 − 3x)e⁻²ˣdx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов x / 4 ⋅ e⁻²ˣ + C (2x − 3) / 4 ⋅ e⁻²ˣ + C 3xe⁻²ˣ + C (5 − 6x) / 4 ⋅ e⁻²ˣ + C (6x − 5) / 4 ⋅ e⁻²ˣ + C Найти интеграл ∫ ⁵√(x³)dx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов 1/5 ⋅ x ⋅ ⁵√(x³) + c 5/8 ⋅ x ⋅ ⁵√(x³) + c 3/5 ⋅ x^(3/5) + c −5/2 ⋅ x^(−2/5) + c 5/8 ⋅ x² ⋅ ⁵√(x³) + c Найти интеграл ∫ aˣ(1 + a⁻ˣ / √(x³))dx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов aˣ / lna − 3/2 ⋅ √x + c aˣ / lna + 3/2 ⋅ √x + c aˣ / lna − 3/2 ⋅ ∛x + c aˣ / lna − 2/2 ⋅ ∛x + c aˣ / lna + 3/2 ⋅ ∛x + c Найти интеграл ∫ cos2xdx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов -1/2 ⋅ sin2x + C 1/2 ⋅ sinx + C cos²2x / 2 + C 1/2 ⋅ sin2x + C sin2x + C Найти интеграл ∫ dx / (√x + 1) Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов ln│√x + 1│+ C 1/2 ⋅ ln│√x + 1│+ C √x + 2ln│√x + 1│+ C 2√x − 2ln│√x + 1│+ C 2√x + 2ln│√x + 1│+ C Найти интеграл ∫ cos²xdx Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов cos³x / 3 + c 1/2 ⋅ x + 1/4 ⋅ sin2x + c 1/2 ⋅ cos³x + c x + sin2x + c 1/2 ⋅ x - 1/4 ⋅ sin2x + c Найти интеграл ∫ dx / (x² + 6x + 13) Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов arcsin(x + 3) + c arcsin((x + 3) / 2) + c arctg(x + 3) + c 1/2 ⋅ arctg((x + 3) / 2) + c 2arctg(x + 3) + c Найти интеграл ∫ dx / √(4 − x²) Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов arcsinx + c arccosx + c arcsin(x/2) + c arctg(x/2) + c 1/2 ⋅ arctg(x/2) + c Найти интеграл ∫ dx / √(x² + 3x) Тип ответа: Одиночный выбор • с выбором одного ....
Файлы условия, демо
Список вопросов
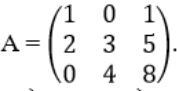
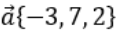

y=c₁e⁶ˣ+c₂e³ˣ
y=c₁e⁻⁶ˣ+c₂eˣ
y=c₁e⁻²ˣ+c₂e⁻³ˣ



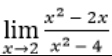
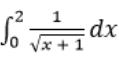
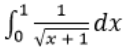

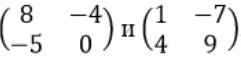
 Вычислите высоту h данного параллелепипеда, если за основание взят параллелограмм, построенный на векторах a и b.
Вычислите высоту h данного параллелепипеда, если за основание взят параллелограмм, построенный на векторах a и b. 
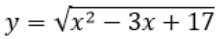
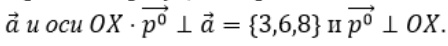
A. Прямые параллельны
B. Прямые перпендикулярны
C. Прямые совпадают
D. k₁=k₂,b₁≠b₂
E. k₁∙k₂=-1
F. k₁=k₂,b₁=b₂
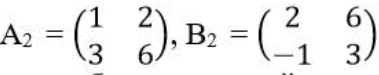
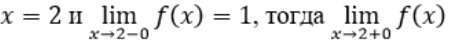
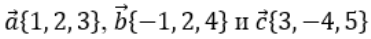
- │a│
- │b│
- │c│
A. a + b
B. b − a
C. kb
D. {a₁ − b₁, a₂ − b₂, a₃ − b₃}
E. {b₁ − a₁, b₂ − a₂, b₃ − a₃}
F. {kb₁, kb₂, kb₃}
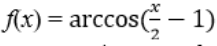
- ((3, 0, 0), (3, 3, 0), (3, 3, 3))
- ((2, 2, 2), (2, 2, 2), (2, 2, 2))
- ((2, 2, 2), (0, 2, 2,), (0, 0, 2))
- ((1, 1, 1), (1, 1, 1), (1, 1, 1), (1, 1, 1))
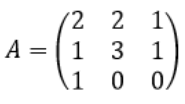
A. Сложение матриц
B. Вычитание матриц
C. Умножение матрицы на число
D. сложение соответствующих элементов матриц
E. вычитание соответствующих элементов матриц
F. умножение всех элементов матрицы на число

Эти вопросы в других коллекциях
Характеристики ответов (шпаргалок) к экзамену























