Статистика (3сем. лекция №5) (805124)
Текст из файла
Облакова Т.В. Лекция №5 (статистика) 2017 (Э2-31,2, Э4-32,3, Э10-31,2)
Лекция №5. Первоначальная обработка статистических данных.
Определение. Все значения, которые может принимать случайная величина  , называют выборочным пространством, или генеральной совокупностью.
, называют выборочным пространством, или генеральной совокупностью.
Выборкой объема  называют
называют  возможных значений случайной величины:
возможных значений случайной величины:  - реализации случайной величины.
- реализации случайной величины.
Определение. Статистикой, называется любая функция от выборки, не зависящая от неизвестных параметров распределения.
Определение. Если выборку упорядочить по возрастанию, то получим вариационный ряд:  ;
;
при этом  -
-  -ая порядковая статистика (функция от выборки)
-ая порядковая статистика (функция от выборки)
Примеры статистик.
1)  - выборочное среднее
- выборочное среднее
2)  – выборочная дисперсия
– выборочная дисперсия
3)  - размах выборки
- размах выборки
Определение 4. Выборочной функцией распределения называется
 ,
,  ,
,  ,
,
То есть  , если ровно
, если ровно  наблюденных значений меньше
наблюденных значений меньше  .
.
 - статистика (при каждом
- статистика (при каждом  ), то есть функция от выборки
), то есть функция от выборки
Пример. Рассмотрим выборку: 1,3,4,6,3,1,7,2,3,7
Строим вариационный ряд: статистический ряд :
статистический ряд :
| | 1 | 2 | 3 | 4 | 6 | 7 |
| Относительные Частоты | | | | | | |
| Относительные накопленные частоты | | | | | | |
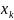 - неповторяющиеся значения;
- неповторяющиеся значения;  - количество элементов выборки, равных
- количество элементов выборки, равных 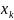 ;
;

Находим эмпирическую функцию распределения:

Свойства эмпирической функции распределения.
1. 
2.  ,
, 
3.  не убывает
не убывает
4.  непрерывна слева
непрерывна слева
Теорема 1. Если взята независимая выборка объема  из генеральной совокупности, имеющей функцию распределения
из генеральной совокупности, имеющей функцию распределения  то
то  дискретная случайная величина, закон распределения которой имеет вид:
дискретная случайная величина, закон распределения которой имеет вид:
 ,
, 
Доказательство. При каждом  индикаторы
индикаторы  – независимые случайные величины с законом распределения:
– независимые случайные величины с законом распределения:


Следовательно,  –распределена по закону Бернулли, то есть
–распределена по закону Бернулли, то есть
 .
.
Следствия.
1. 
2. 

Теорема 2 (Гливенко-Кантелли (б/д)) Если  – независимая выборка неограниченного объема, то при
– независимая выборка неограниченного объема, то при 

 с вероятностью 1.
с вероятностью 1.
Группировка выборки
Определение. Группированной выборкой называется выборка, разбитая на интервалы следующим образом:
|
|
|
| ||
|
|
|
|
Здесь  ,
,  ,
,  ,
,  - количество элементов выборки, попадающих в интервал
- количество элементов выборки, попадающих в интервал  , при этом
, при этом 
Для группированной выборки также находят характеристики
 - выборочное среднее,
- выборочное среднее,
где  - середина
- середина  -го интервала
-го интервала
 - выборочная дисперсия
- выборочная дисперсия
Для группированной выборки также можно ввести выборочную функцию распределения: 
Определение. Гистограммой относительных частот называется совокупность прямоугольников со сторонами  и
и  .
.
При этом площадь каждого прямоугольника равна 
- статистическая вероятность принять значение в интервале  .
.
Суммарная площадь фигуры естественно равна 1
Таким образом, для абсолютно непрерывных случайных величин гистограмма служит приближением графика плотности вероятностей
Метод моментов.
Пусть  –неизвестный параметр для известного закона распределения.
–неизвестный параметр для известного закона распределения.
Вычисляются  эмпирических и
эмпирических и  теоретических моментов и решается система из
теоретических моментов и решается система из  уравнений с
уравнений с  неизвестными.
неизвестными.

Примеры. 1. Пуассоновский закон с неизвестным параметром  .
.
Тогда  – математическое ожидание (первый теоретический момент)
– математическое ожидание (первый теоретический момент)
 - выборочное среднее (первый эмпирический момент)
- выборочное среднее (первый эмпирический момент)
Следовательно,  – оценка параметра
– оценка параметра  , построенная по выборке
, построенная по выборке
2. Пусть  –выборка из нормального распределения с неизвестными параметрами
–выборка из нормального распределения с неизвестными параметрами  и
и  .
.
Теоретические моменты:  ,
, 
Приравниваем к эмпирическим моментам и находим оценки:

Задача 1. Первоначальная обработка статистических данных
По данной выборке
1. Найдите крайние члены вариационного ряда и размах выборки
2. Осуществите группировку данных (количество интервалов находим по правилу Стерджеса)
3. По сгруппированным данным постройте гистограмму относительных частот
4. Найдите эмпирическую функцию распределения и постройте ее график
5. Вычислите выборочное среднее и выборочную дисперсию.
Демонстрационный вариант:
| 1.913 | 2.875 | 3.302 | 2.338 | 3.967 | 0.702 | 0.655 | 2.038 | 0.342 | 0.331 |
| 8.936 | 7.5 | 0.86 | 1.763 | 3.297 | 2.003 | 3.036 | 6.432 | 3.267 | 2.78 |
| 0.679 | 2.7 | 0.927 | 3.094 | 2.928 | 2.274 | 4.5 | 3.229 | 5.441 | 2.86 |
| 8.084 | 4.336 | 3.673 | 1.261 | 1.217 | 0.383 | 6.351 | 0.561 | 0.276 | 3.415 |
| 2.626 | 1.753 | 2.088 | 0.552 | 4.465 | 5.842 | 6.888 | 1.189 | 0.454 | 5.123 |
| 3.136 | 0.25 | 3.536 | 0.369 | 0.859 | 8.418 | 3.623 | 2.261 | 2.289 | 2.373 |
| 3.884 | 3.107 | 0.02 | 0.354 | 6.632 | 4.586 | 1.594 | 2.683 | 10.39 | 0.648 |
| 0.471 | 10.102 | 0.094 | 0.192 | 0.471 | 6.658 | 4.263 | 0.049 | 4.102 | 0.818 |
| 0.617 | 1.39 | 1.527 | 5.405 | 2.492 | 5.335 | 0.521 | 1.716 | 0.489 | 0.228 |
| 2.839 | 2.647 | 1.243 | 5.501 | 1.115 | 7.52 | 4.539 | 1.494 | 0.865 | 0.869 |
Характеристики
Тип файла документ
Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.
Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.
Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.































