Book5 (1000295), страница 10
Текст из файла (страница 10)
σ 3 т— тепловая проводимость установочных элементов:
где п — число элементов; λ — коэффициент теплопроводности мате-
риала; l— длина установочных элементов по направлению теплового
потока; SCP — площадь средней изотермической поверхности, перпен-
дикулярной направлению теплового потока;
σ с к — тепловая проводимость стенок кожуха;
где λ с к— коэффициент теплопроводности материала корпуса; δ с к—
толщина стенки; S к вн, S к н — площади внутренней и наружной повер-
хностей корпуса;
σкк— тепловая проводимость от наружной поверхности корпуса к
среде для конвективной теплопередачи:
σк.к = αкSк.н
где α к — коэффициент теплопередачи; σкл=αлSкн — тепловая про-
водимость от наружной стенки корпуса к среде для теплопередачи из-
лучением; α л — коэффициент теплопередачи излучением.
Расчет показателей теплового режима блоков может быть выполнен
методом последовательных приближений или тепловой характеристи-
ки. В ориентировочных расчетах для определения тепловой проводи-
мости ст 3 от центра нагретой зоны к ее поверхности можно воспользо-
ваться [20] усредненными значениями эквивалентных коэффициентов
222
теплопроводности нагретой зоны: λ.х = λ,z = 0,35 Вт/(м • К),
λY, =0,09 Вт/(м • К). Оси координат Ох и Oz лежат в плоскости плат
функциональных ячеек, ось Оу — перпендикулярна плоскостям плат.
Для условий теплообмена в ограниченном пространстве коэффици-
ент теплопередачи излучением αлз может быть принят равным
7 Вт/(м2-К).
Порядок расчета тепловой контактной проводимости σ тк изложен в
разд. 5.4.1.
При малой толщине стенки (δ с к = 1,5...2 мм) тепловым сопротивлением стенок корпуса, выполненного из металлических сплавов с высоким коэффициентом теплопроводности, обычно пренебрегают. Однако если используется корпус из пластмассы, то тепловую проводимость стенок σ с к необходимо учитывать.
Для определения конвективного α к и лучевого αл коэффициентов
теплопередачи в условиях неограниченного пространства (теплообмен
между наружной стенкой кожуха и окружающей средой) можно вос-
пользоваться номограммами рис. 5.9 и 5.10.
5.5.2. Расчет собственного и наведенного перегрева
Перегрев любой точки или области конструкции является результа-
том взаимодействия источников тепла. Он складывается из собственно-
го и наведенного перегревов. Собственный перегрев определяется дей-
ствием источника тепла, расположенного в j-й точке при условии, что
остальные источники выключены. Наведенный перегрев обусловлен
действием всех источников тепла, кроме расположенного в j-й точке.
Для расчета собственного и наведенного перегревов тепловая мо-
дель должна быть детализирована до выделения отдельных источни-
ков тепла или групп источников. Решение задачи иллюстрируется на
примере блока разъемного типа, когда каждая функциональная ячейка
рассматривается как нагретая зона с распределенными в ней источни-
ками тепла. Данная модель позволяет рассчитывать собственный и на-
веденный перегревы функциональных ячеек и получать распределение
температуры внутри нагретой зоны блока.
Схематическое изображение конструкции блока приведено на
рис. 5.37.
В металлическом корпусе 1 размещено m функциональных ячеек,
собранных на корпусированных ИС. Каждая ячейка представляет собой
нагретую зону. Поверхности всех т нагретых зон — изотермические с
223

той зоны h3i = Ki3b + δП , где Ki3 —
коэффициент заполнения i-й функ-
циональной ячейки; b — шаг размещения ячеек в блоке; δп — толщина печатной платы.
Из-за малых воздушных зазоров
теплообмен между функциональны-
ми ячейками (2...3 мм) можно рас-
сматривать как процесс передачи
тепла теплопроводностью через ог-
раниченную многослойную стенку.
Рис. 5.37. Схемотехническое
изображение блока кассетной
конструкции
От плат функциональных ячеек ккорпусу и от корпуса к окружающей среде тепло передается конвекцией и излучением. Поверхности корпуса и функциональных ячеек (нагретых зон) принимают за изотермические со среднеповерхностными
температурами tK и t3i . Кроме того, считают, что функциональные
ячейки однотипны по конструкции, коэффициенты заполнения всех
плат одинаковы, воздушный зазор между ячейками b1 , =b -h3i постоя-
нен по всей площади платы.
Перегрев поверхности каждой ячейки складывается из собственно-
го перегрева Δ t., обусловленного действием только собственных источников тепла Р i и наведенного Δ tf H в результате действия источников тепла всех ФЯ, кроме i-й.
Тепловые схемы блока для расчета собственного и наведенного пе-
регревов приведены на рис. 5.38 и 5.39 соответственно. На схемах приняты следующие обозначения: t c — температура окружающей среды; Δ t к — перегрев корпуса блока; t3,-, Δ13,- — среднеповерхностная температура и перегрев i-й функциональной ячейки; R σ0 — тепловое сопротивление воздушной прослойки между крайними ячейками и кожухом; R σ — тепловое сопротивление между соседними ячейками; R B тепловое сопротивление воздушных прослоек между торцевыми поверхностями ФЯ и кожухом.
Предполагается, что тепловой поток Р i рассеиваемый нагретой зо-
ной i-й ФЯ, распространяется влево и вправо от ячейки.
При этом часть теплового потока, идущая в левую сторону, Рiл об-
ратно пропорциональна тепловому сопротивлению левой от i-й функ-
циональной ячейки ветви Рiл. Составляющая теплового потока, рас-
224

Рис. 5.38. Тепловая схема блока для расчета собственного перегрева:
а — исходная схема; б — преобразованная
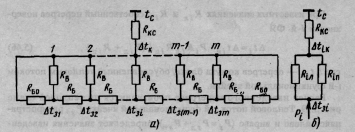
Рис. 5.39. Тепловая схема блока для расчета наведенного перегрева
пространяющаяся в правую сторону, Рiп обратно пропорциональна
тепловому сопротивлению правой ветви Рiп (рис. 5.38, б).
Как следует из тепловой схемы рис. 5.38, а,
Riл =[ R(i-1)л(Rв + Rσ)+RвRσ]/(R(i-1)л + Rв). (5.44)
R i.п = [(Rб+R(i+1)п)Rв]/(Rв+Rб+R(i + 1)П), (5.45)
гдеR1л = Rб0, i=l, 2 т.
225
При известных значениях R i л и R iп собственный перегрев поверхности i-й ФЯ
Δti,. = Δtik + PiRiл.Riп/(Riл+ Riп) (5-46)
где Δ t {к — перегрев кожуха блока, обусловленный тепловым потоком
1-й функциональной ячейки.
Расчет наведенного перегрева производится по тепловой схеме
рис. 5.39. Тепловой поток s-й функциональной ячейки РS , распространяясь влево и вправо (РS=PSJ1 + Psn), определяет значения наведенных на соседних ячейках перегревов. Из схемы рис. 5.39
PSJ1=(ΔtS - ΔtSK)/RSЛ (5-47)
PSП=(ΔtS - ΔtK)/RSП (5.48)
Входящие в (5.47) и (5.48) тепловые сопротивления PSJ1и PSП рас-
считываются по формулам (5.44) и (5.45), собственный перегрев s-й
ячейки Δ ts — по формуле (5.46).
Перегревы, наведенные на функциональные ячейки, расположен-
ные слева от s-й, определяются соотношениями:
ΔtS(S-1)=ΔtS-PSЛRσ;P*(S-1)Л=(ΔtS(S-1)-ΔtSK)/RB
P(S-1)Л=PSЛ- P*(S-1)Л; ΔtS(S-2)= ΔtS(S-1)- P(S-1)ЛRσ;…
…;P*2Л= (ΔtS2-ΔtSK)/RB; P2Л = P3Л-P*2Л ; ΔtS1= ΔtS2-P2ЛRσ
Перегревы, наведенные на ФЯ, расположенные справа:
P*SП=(ΔtS-ΔtSK)/RB;P(S+1)П= PSП- P*SП;
ΔtS(S+1)=ΔtS-P(S+1)ПRσ; P*(S+1)П=(ΔtS(S+1)-ΔtSK)/RB
P(S+2)П= P(S+1)П-P*(S+1)П;…;PmП= P(m-1)П- P*(m-1)П
ΔtSm= ΔtS(m-1)-PmПRσ
226
Перегрев поверхности i-й функциональной ячейки с учетом собст-
венного и наведенного перегревов согласно принципу суперпозиции
можно найти как
Тепловое сопротивление R 6 0 обусловлено конвективно-кондуктивной и лучевой теплопередачами через воадушную прослойку между
боковой поверхностью крайней платы и внутренней боковой стенкой
кожуха:
RбО=Δy/(кпλBScр + αЛSПЛΔу),
где Δ у — толщина воздушной прослойки; к п — поправочный коэффициент на конвективную теплопередачу; λв — коэффициент теплопроводности воздуха; Sср = 0,5(Sпл + Sстб) — площадь средней изотермической поверхности; S ПЛ = lплxlпyx — площадь поверхности платы ФЯ; 1ПЛХ, /ПЛ2 — геометрические размеры платы; S стб— площадь внутренней боковой стенки кожуха; α л — коэффициент теплопередачи излучением.
Тепловое сопротивление R B характеризует конвективно-кондуктив-
ную и лучевую теплопередачи между торцевой поверхностью функци-
ональной ячейки и внутренней поверхностью кожуха, охватывающей
торцевые поверхности ФЯ (нагретых зон):
Rв = ΔX/(кпλвSср + αлSiтΔх),
где Δx — средняя толщина воздушной прослойки между торцевой поверхностью нагретых зон и внутренней поверхностью кожуха; SCP =
= 0,5(SiT + SКВН) — площадь средней изотермической поверхности;
SiT = 2 h 3i(lплх +lплz) — площадь торцевой поверхности i-й нагретой
зоны; S к вн— площадь внутренней поверхности кожуха, охватывающей
торцевые поверхности нагретых зон.
Тепловое сопротивление между соседними платами R σ = b/λуSпл,где λy, — эквивалентный коэффициент теплопроводности нагретой зоны блока по направлению y- Определение λy, производится в результа-
















