Ответы на вопросы из коллекции "☀️Железобетонные и каменные конструкции, пространственные несущие системы | ТУлГУ сборник ответов на все тесты☀️"

По какой схеме работает каркас здания приведенный на рисунке в поперечном направлении (1 – рамы, 2 – диафрагмы)?

• По каркасной.
• По диафрагменной.
• По рамной.
• По рамно-связевой
• По связевой.

По каким формулам рассчитывается прочность каменного элемента армированного сетками при центральном сжатии?

• Aiₛ = Mi/(0,9h₀iRₛ) , где Aiₛ – расчетное сопротивление арматуры; σ`ₛ = αM(x – a`)/Wred определяется в зависимости от гибкости элемента и упругой характеристики кладки с сетчатым армированием i–м, где α – упругая характеристика для неармированной кладки; Mi – средний предел прочности неармированной и армированной сетками кладок h₀i – , Aₛ = –0,25(hf + bf) + 0,5 √Ncol/(Rb+Pef); Aₛ = коэффициент, учитывающий вид кладки; Rₛₙ – нормативное сопротивление арматуры, которое принимается с учетом коэффициента условия работы γcs ≤ 1.
• N ≤ mgφRₛₖA , где Rₛₖ ≤ 2R – при кладке на растворах марки М25 и выше, при высоте ряда не более 150 мм: Rₛₖ = R + 2Rₛμ/100 ≤ 2R ; при кладке на растворах марки менее М25: Rₛₖ = R + (2Rₛμ/100)(R₁/R₂₅) ≤ 2R ; Aⁱₛ – расчетное сопротивление арматуры; R₁ – фактическое расчетное сопротивление сжатию кладки; R₂₅ – для кладки на растворе марки М25; σ` = αM(x – a`)/Wred определяется в зависимости от гибкости элемента и упругой характеристики кладки с сетчатым армированием i–м , где α – упругая характеристика для неармированной кладки; Mi – средний предел прочности неармированной и армированной сетками кладок h₀i – , Aₛ = –0,25(hf + bf) + 0,5√Ncol/(Rb + Pef) ; Aₛ = коэффициент, учитывающий вид кладки; Rₛₙ – нормативное сопротивление арматуры, которое принимается с учетом коэффициента условия работы γcs ≤ 1 .
• сN ≤ mgφ₁RskbAc , или для прямоугольных сечений при e₀ ≤ 0,17h : N ≤ mgφ₁RskbA (1 – 2e₀/h) , где Rskb = R + (2Rₛμ/100) (1 – 2e₀/y) – при кладке М25 и выше, или Rskb = R + (2Rₛμ/100) (R₁/R₂₅) (1 – 2e₀/y) .
• N ≤ mgφRskA , где Rsk ≤ 2R – при высоте ряда не более 150 мм: Rsk = R + 2Rsμ/100 ≤ 2R ; Ai s – расчетное сопротивление арматуры; R₁ фактическое расчетное сопротивление сжатию кладки; R₂₅ – для кладки на растворе марки М25; σ`s = αM(x – a`)/Wred определяется в зависимости от гибкости элемента и упругой характеристики кладки
• N ≤ mgφ₁RskbAcω , или для прямоугольных сечений при e₀ ≤ 0,17h : N ≤ mgφ₁RskbA (1 – 2e₀/h) ω , где Rskb = R + (2Rₛμ/100) (1 – 2e₀/y) – при кладке М25 и выше, или Rskb = R + (2Rₛμ/100) (R₁/R₂₅) (1 – 2e₀/y) .

На каком рисунке изображена ребристая плита без предварительного напряжения арматуры?

Какую цель преследуют при расчете по первой группе предельных состояний?

• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) потери устойчивости формы конструкции или ее положения; в) усталостного разрушения конструкций, находящихся под воздействием многократно повторяющейся нагрузки; г) развития чрезмерных деформаций.
• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) потери устойчивости формы конструкции или ее положения; в) образования трещин в бетоне; г) развития чрезмерных деформаций.
• Чтобы не допустить: а) развития чрезмерных деформаций; б) образования трещин в бетоне; в) чрезмерного раскрытия трещин.
• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) чрезмерного раскрытия трещин; в) образования трещин в бетоне; г) развития чрезмерных деформаций.
• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) потери устойчивости формы конструкции или ее положения; в) усталостного разрушения конструкций, находящихся под воздействием многократно повторяющейся нагрузки; г) разрушения от совместного действия силовых факторов и неблагоприятных влияний внешней среды, например агрессивной среды или замораживания и оттаивания

Какую цель преследуют при расчете по второй группе предельных состояний?

• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) чрезмерного раскрытия трещин; в) образования трещин в бетоне; г) развития чрезмерных деформаций.
• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) потери устойчивости формы конструкции или ее положения; в) усталостного разрушения конструкций, находящихся под воздействием многократно повторяющейся нагрузки; г) развития чрезмерных деформаций.
• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) потери устойчивости формы конструкции или ее положения; в) усталостного разрушения конструкций, находящихся под воздействием многократно повторяющейся нагрузки; г) разрушения от совместного действия силовых факторов и неблагоприятных влияний внешней среды, например агрессивной среды или замораживания и оттаивания.
• Чтобы не допустить: а) хрупкого, пластического или вязкого разрушения; б) потери устойчивости формы конструкции или ее положения; в) образования трещин в бетоне; г) развития чрезмерных деформаций.
• Чтобы не допустить: а) развития чрезмерных деформаций; б) образования трещин в бетоне; в) чрезмерного раскрытия трещин

Какие формулы используются, чтобы определить коэффициент, учитывающий влияние увеличения начального эксцентриситета приложения сжимающей продольной силы во внецентренно сжатых ЖБК η?

• η = 1/(1 – N/Ncr), где Ncr – условная критическая продольная сила, учитывающая возможность потери устойчивости конструкции, работающей с трещинами.
• η = 1/(1 – Q/Qcr), где Qcr – условная критическая поперечная сила, учитывающая возможность потери устойчивости конструкции, работающей с трещинами.
• η = 1,5.
• η = 1/(1 – M/Mcr), где Mcr – условный критический момент, учитывающая возможность потери устойчивости конструкции, работающей с трещинами.
• η = 0,9.

Какие требования предъявляются к ЖБК по трещиностойкости и сколько категорий трещиностойкости известно?
Выберите один ответ:

• В конструкциях первой категории трещиностойкости трещины не допускаются. В конструкциях второй категории трещиностойкости допускается ограниченное по ширине кратковременное раскрытие трещин, но требуется их надежное закрытие при отсутствии кратковременной нагрузки. В конструкциях третьей категории трещиностойкости образование трещин в стадии эксплуатации допустимо, но ограничивается ширина их раскрытия, различная при кратковременном и длительном действии нагрузки. В конструкциях четвертой категории трещиностойкости образование трещин в стадии эксплуатации допустимо, но ограничивается ширина их раскрытия, различная при кратковременном и длительном действии нагрузки, а также допускается местное оголение арматуры.
• В конструкциях первой категории трещиностойкости трещины не допускаются. В конструкциях второй категории трещиностойкости допускается ограниченное по ширине кратковременное раскрытие трещин, но требуется их надежное закрытие при отсутствии кратковременной нагрузки. В конструкциях третьей категории трещиностойкости образование трещин в стадии эксплуатации допустимо, но ограничивается ширина их раскрытия, различная при кратковременном и длительном действии нагрузки.
• В конструкциях первой категории трещиностойкости трещины не допускаются. В конструкциях второй категории трещиностойкости допускается ограниченное по ширине кратковременное раскрытие трещин, но требуется их надежное закрытие при отсутствии кратковременной нагрузки.
• В конструкциях первой категории трещиностойкости трещины не допускаются. В конструкциях третьей категории трещиностойкости образование трещин в стадии эксплуатации допустимо, но ограничивается ширина их раскрытия, различная при кратковременном и длительном действии нагрузки, а также допускается местное оголение арматуры.
• В конструкциях первой категории трещиностойкости трещины не допускаются. В конструкциях второй категории трещиностойкости допускается ограниченное по ширине кратковременное раскрытие трещин, но требуется их надежное закрытие при отсутствии кратковременной нагрузки. В конструкциях третьей категории трещиностойкости образование трещин в стадии эксплуатации допустимо, но ограничивается ширина их раскрытия, различная при кратковременном и длительном действии нагрузки, а также допускается местное оголение арматуры

Какие стадии напряженно-деформированного состояния проходят изгибаемые ЖБК?

• Стадия работы без трещин; стадия работы с трещинами; стадия усадки.
• Стадия работы с трещинами; стадия разрушения.
• Стадия работы без трещин; стадия разрушения.
• Стадия работы без трещин; стадия работы с трещинами.
• Стадия работы без трещин; стадия работы с трещинами; стадия разрушения.

Какие расчетные условия прочности необходимы при расчете нормального сечения для элементов прямоугольного профиля с двойным ненапрягаемым армированием при ξ ≤ ξR и при x > 0 (задачи проверки прочности)?

• RsAs = Rb bx + RscA`s; M ≤ Rb bx (h₀ – 0,5x) + RscA`s(h₀ – a`); RsAs = Rb bh₀ξ + RscA`s; M ≤ A₀Rb bh₀² + RscA`s(h₀ – a`).
• M ≤ WredRs; RsAs = Rb bh₀ξ + RscA`s; M ≤ RbWred (h₀ – 0,5x).
• RsAs = Rb bx + RscA`s; M ≤ Rb bx(h₀ – 0,5x); M ≤ RsAs(h₀ – 0,5x).
• RsAs = Rb bx + RscA`s; M ≤ WplRbt; M ≤ RsAs(ξ – 0,5x).
• RbAs = Rs bx; RsAs = Rb bh₀ξ + RscA`s; M ≤ RsAs(ξ – 0,5x)

Какие расчетные условия используются при расчете прочности наклонных сечений на действие наклонных сжимающих напряжений?

• Q ≤ φfφb2Rbbh₀, где φf = 0,75(b`f – b) h`f/bh₀ ≤ 0,5; α = Es/Eb; μw = Asw/bS; b`f ≤ b + 3h`f; φb2 = 2.
• Q ≤ φb3(1+φf+φn)Rbtbh₀, где φb3 = 0,6; φf = 0,75(b`f – b) h`f/bh₀ ≤ 0,5; b`f ≤ b + 3h`f; φn = 0,1N/Rbtbh₀ ≤ 0,5.
• Q ≤ φfφb1Rbbh₀, где φf = (b`f – b) h`f/bh₀; α = Es/Eb; μw = Asw/bS; φb1 = 1 – βRb.
• Q ≤ 0,3φw1φb1Rbbh₀, где φw1 = 1 + 5αμw ≤ 1,3; α = Es/Eb; μw =Asw/bS; φb1 = 1 – βRb.
• Q ≤ φb2(1+φf+φn)Rbtbh₀², где φb2 = 2; φf = 0,75(b`f – b) h`f/bh₀ ≤ 0,5; b`f ≤ b + 3h`f; φn = 0,1N/Rbtbh₀ ≤ 0,5.

Какая стадия работы сжатой кладки изображена на рисунке?

• Пятая.
• Третья.
• Вторая.
• Четвертая
• Первая.

Какая расчетная длина сжатого каменного элемента принимается при следующем закреплении на опорах?

• Af = Ncol/(Rb – γbHef) ;
• l₀ = 0,7H .
• γb = 25 ;
• h₀ = –0,25(hf + bf) + 0,5 √Ncol/(Rbt+Pef) ;
• Pef = Ncol/Af – ;

Как определить расчетные сопротивления бетона, зная нормативные характеристики?

• Rb = Rbn/γbc; Rbt = Rbtnγbt.
• Rb = Rbn/γbc; Rbt = Rbtn/γbt.
• Rb = Rbn; Rbt = Rbtn.
• Rb = Rbnγbc; Rbt = Rbtnγbt.
• Rb = Rbnγbc; Rbt = Rbtn/γbt

Как определить предельные составляющие усилий, действующих в горизонтальном нормальном сечении железобетонной диафрагмы?

• r = Wpl /[Ab + 2(αₛAₛ + αₚAₛₚ + αₛA`ₛ + αₚA`ₛₚ)] ; r = φWred/Ared ; φ = 0,7 .
• Nc = α·Rb·A ; Ncrc = RbtA + RₛAₛ ; Ncrc = RbtA .
• r = Wpl /[Ab + 2(αₛAₛ + αₚAₛₚ + αₛA`ₛ + αₚA`ₛₚ)] ; φ = 1 ; φ = 1,6 – σb/Rb,ser .
• Nc = α·Rb·A ; Ncrc = RₛAₛ .
• Nc = α·Rb·A ; Ny = α·Rb·Ay ; [Ab + 2(αₛAₛ + αₚAₛₚ)] + P .

Как определить максимальный прогиб К-й диафрагмы параллельной оси У от поной нагрузки?

• RₛAₛ = Rb bh₀A₀.
• ξ = x/h₀.
• AR = (1 – 0,5ξR)ξR.
• M ≤ ξRb bh²₀.
• A₀ = (1 – 0,5ξ)ξ.

Как определить коэффициент снижения жесткости диафрагмы за счет податливости горизонтальных швов, если h – высота этажа; Ab1 – площадь поперечного (горизонтального) сечения стенки диафрагмы; h2 – суммарная высота растворных швов в пределах одного этажа; x ≤ 0 соответственно, модули упругости бетона стенки диафрагмы и шва; M ≤ RsAs(h0 – a`) , M ≤ (γs6RspAsp + RsAs)(h0 – a`s) площадь горизонтального сечения растворного шва; x1 = (–RscA`s + RsAs)/Rbb ≤ a` высота всей диафрагмы; x2 = RsAs/Rbb поперечный размер в направлении наибольшей жесткости?

• RscA`s (h0 – a`s) .
• M ≤ Rbbx1 (h0 – 0,5x1) , где x = (–0,5RscA`s + RsAs)/Rbb ≤ a` относительная высота столба диафрагм; M ≤ Rb bx (h0 – 0,5x) .
• M ≤ 0,5 (A0 + AR) Rbbh0²
• M ≤ Rbbx2 (h0 – 0,5x2)
• x1 = (–0,5RscA`s + RsAs)/Rbb > a`
  

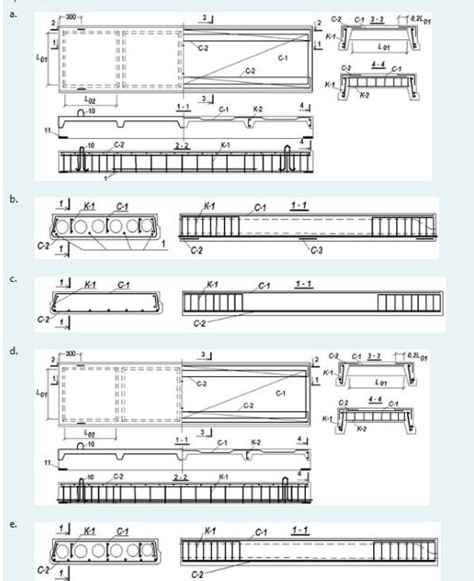
Как определить касательные напряжения в стенках ядра жесткости на участках с проемами в сечении i-го столба, если δ, t, b – толщина стенки ядра и его разметы в плане?

• Nₜₒₜ = P , где Q –поперечная сила в горизонтальном сечении ядра от изгиба; I – момент инерции в сплошной зоне ядра относительно оси, проходящей через центр тяжести всего ядра; Mr = N(e₀+r) момент чистого кручения, воспринимаемый сечением ядра.
• Mₛ – , где Q –поперечная сила в горизонтальном сечении ядра от изгиба; I – момент инерции в сплошной зоне ядра относительно оси, проходящей через центр тяжести всего ядра; Ii – момент инерции σₛₚ⁰≤0,7Rs,ser –того столба относительно собственной центральной оси перпендикулярной плоскости изгиба этого столба; Mr = N(e₀+r) момент чистого кручения, воспринимаемый сечением ядра.
• τ = (Qs/I + Msω/bt)/2δ , где Q –поперечная сила в горизонтальном сечении ядра от изгиба; S, – статический момент отсеченных площадей сечения ядра; I – момент инерции в сплошной зоне ядра относительно оси, проходящей через центр тяжести всего ядра; Mr = N(e₀ + r) момент чистого кручения, воспринимаемый сечением ядра.
• Mₛ = M + Peₛₚ , где Q –поперечная сила в горизонтальном сечении ядра от изгиба; S, – статический момент отсеченных площадей сечения ядра; I – момент инерции в сплошной зоне ядра относительно оси, проходящей через центр тяжести всего ядра; Mr = N(e₀+r) момент чистого кручения, воспринимаемый сечением ядра.
• τi = 2MiSi/Iih₂δ , где Q –поперечная сила в горизонтальном сечении ядра от изгиба; Si – статический момент отсеченных площадей сечения i-того столба ядра; I – момент инерции в сплошной зоне ядра относительно оси, проходящей через центр тяжести всего ядра; Ii – момент инерции σₛₚ⁰≤0,7Rs,ser –того столба относительно собственной центральной оси перпендикулярной плоскости изгиба этого столба; Mr = N(e₀+r) момент чистого кручения, воспринимаемый сечением ядра.

Как определить изгибающий момент от вертикальной нагрузки в К-й диафрагме параллельной оси У?

• M_ky^eq(x) = x _ky^eq/∑i=1nBiz .
• M_ky^eq(x) = xBkz (m_ky^eq/∑i=1nBiz + T·zk/Bω)
• M_ky^eq(x) = x T·zk/Bω .
• M_ky^eq(x) = xBkz T·zk/Bω .
• M_ky^eqx) = xBkz m_ky^eq/∑i=1nBiz .

Как определить длину анкеровки продольных рабочих стержней, обрываемых в пролете при наличии в изгибаемой ЖБК, имеющей поперечные стержни?

• W = Q₁ / 2qsw₁ + 25d ≤ 20d, где Q₁, qsw₁ – расчетная поперечная сила и усилие, воспринимаемое поперечными стержнями в месте теоретического обрыва.
• W = φb₃ (1 + φf + φₙ) Rbt bh₀ / 2qsw₁ + 5d ≤ 20d, где Q₁, qsw₁ – расчетная поперечная сила и усилие, воспринимаемое поперечными стержнями в месте теоретического обрыва.
• W = Q₁/2q₁ + 5d ≤ 20d, где Q₁, q₁ – расчетная поперечная сила и погонной усилие, действующее в месте теоретического обрыва.
• W = Q₁/2qsw₁ + 5d ≤ 20d, где Q₁, qsw₁ – расчетная поперечная сила и усилие, воспринимаемое поперечными стержнями в месте теоретического обрыва.
• W = Qb/2qsw₁ + 5d ≤ 20d, где Qb, qsw₁ – поперечная сила, воспринимаемая сжатой зоны бетона и усилие, воспринимаемое поперечными стержнями в месте теоретического обрыва.

Как определить граничную относительную высоту сжатой зоны бетона для ненапрягаемых ЖБК?

Как определить высоту первой ступени отдельного центрально загруженного фундамента под колонну?

• h₀₁ ≥ 200 мм.
• h₀₁ ≤ 300 мм.
• Q = Pef (l₁ – C) bf ≤ φb₄ Rbt bf h₀₁² / C, где правая часть неравенства принимается не менее φb₃ Rbt bf h₀₁ и не более 2,5 Rbt bf h₀₁; φb₃ = 0,6; φb₄ = 1,5; h₀₁ – рабочая высота сечения первой ступени; С – длина горизонтальной проекции наклонного сечения; Pef = Ntot / Af, Ntot – расчетное усилие с учетом массы колонны в фундаменте.
• Q = Pef (l₁ – C) bf ≤ 2,5Rbt bf h₀₁, где правая часть неравенства принимается не менее φb₃ Rbt bf h₀₁; φb₃ = 0,6; φb₄ = 1,5; h₀₁ – рабочая высота сечения первой ступени; С – длина горизонтальной проекции наклонного сечения; Pef = Ntot / Af, Ntot – расчетное усилие с учетом массы колонны в фундаменте.
• Q = Pef (l₁ – C) bf ≤ φb₃ Rbt bf h₀₁, где Pef = Ntot / Af, Ntot – расчетное усилие с учетом массы колонны в фундаменте.

Как классифицируются плоские железобетонные перекрытия?

• а) распорные; б) безраспорные; в) арочные; г) балочные; в) безбалочные.
• а) арочные; б) балочные; в) безбалочные; г) сборные; д) монолитные; е) сборномонолитные.
• а) сборные; б) монолитные; в) сборно-монолитные.
• а) балочные сборные; б) ребристые монолитные с балочными плитами, работающими в одном направлении; в) ребристые монолитные с плитами опертыми по контуру; г) балочные сборно-монолитные; д) безбалочные сборные;е) безбалочные монолитные.
• а) сборные; б) монолитные; в) сборно-монолитные; г) балочные; в) безбалочные.

Как классифицируются железобетонные фундаменты по по способу возведения?

• а) монолитные; б) сборные.
• а) сплошные – под всем зданием или сооружением; б) фундаменты на естественных основаниях; в) фундаменты на сваях; г) монолитные; д) сборные.
• а) отдельные фундаменты – под каждой колонной; б) ленточные – под рядами колонн в одном или двух направлениях; в) ленточные фундаменты под несущими стенами; г) сплошные – под всем зданием или сооружением; д) фундаменты на естественных основаниях; е) фундаменты на сваях.
• а) монолитные; б) сборные; в) сборно-монолитные.
• а) отдельные фундаменты – под каждой колонной; б) ленточные – под рядами колонн в одном или двух направлениях; в) ленточные фундаменты под несущими стенами; г) монолитные; д) сборные.

Как классифицируются железобетонные фундаменты по конструктивным признакам?

• а) сплошные – под всем зданием или сооружением; б) фундаменты на естественных основаниях; в) фундаменты на сваях; г) монолитные; д) сборные.
• а) отдельные фундаменты – под каждой колонной; б) ленточные – под рядами колонн в одном или двух направлениях; в) ленточные фундаменты под несущими стенами; г) сплошные – под всем зданием или сооружением; д) фундаменты на естественных основаниях; е) фундаменты на сваях.
• а) отдельные фундаменты – под каждой колонной; б) ленточные – под рядами колонн в одном или двух направлениях; в) ленточные фундаменты под несущими стенами; г) монолитные; д) сборные.
• а) монолитные; б) сборные.
• а) монолитные; б) сборные; в) сборно-монолитные.

Что физически представляет собой бетон?

• Крупнозернистый литой материал.
• Капиллярно-пористый материал, в котором нарушена сплошность.
• Монолитный литой материал.
• Мелкозернистый литой материал.
• Капиллярно-пористый материал, в котором нарушена сплошность и присутствуют в основном две фазы – твердая и газообразная

Что такое передаточная прочность бетона Rbp?

• Кубиковая прочность бетона в момент выпуска ЖБК с завода ЖБИ.
• Кубиковая прочность бетона перед разрушением.
• Кубиковая прочность бетона в момент распалубки ЖБК.
• Кубиковая прочность бетона в момент поступления ЖБК на строительную площадки.
• Кубиковая прочность бетона в момент его обжатия, т. е. отпуска арматуры с упоров или начала натяжения арматуры на бетон.

Что такое номинальный размер конструкции?

• Размер конструкций в осях
• Размер, установленный при помощи геодезических приборов.
• Фактический размер конструкции.
• Размер, учитывающий допуски при изготовлении.
• Средний размер конструкции из всей партии.

Что такое натурный размер конструкции?

• Размер, отличающийся от номинального на величину зазора.
• Размер, установленный при помощи геодезических приборов.
• Размер конструкций в осях.
• Размер конструкций в осях.
• Фактический размер, который отличается от конструктивного на величину допуска изготовления

Что такое модуль деформаций бетона?

• Это отношение полных деформаций к величине соответствующих напряжений.
• Тангенс угла наклона касательной к диаграмме деформирования в точке соответствующей заданному уровню напряжений σb.
• Тангенс угла наклона секущей на диаграмме деформирования в точке с заданным напряжением.
• Тангенс угла наклона касательной к диаграмме деформирования на начальном участке.
• Это отношение напряжений к пластическим деформациям.

Что такое конструктивный размер конструкции?

• Размер, учитывающий допуски при изготовлении.
• Размер, отличающийся от номинального на величину зазора
• Размер конструкций в осях.
• Средний размер конструкции из всей партии.
• Фактический размер конструкции.

Что такое класс бетона по прочности на сжатие?

• Кубиковая прочность бетонных образцов с размером ребра 15 см.
• Временное сопротивление сжатию бетонных кубиков с размерами ребра 15 см, испытанных через 28 суток твердения.
• Прочность бетонных призм на сжатие.
• Гарантированная кубиковая прочность с обеспеченностью 95%.
• Временное сопротивление сжатию бетонных кубиков с размерами ребра 15 см, испытанных через 28 суток твердения при температуре 20 ± 20С при нормальном давлении, влажности и с учетом статистической изменчивости прочности.

Что такое класс бетона по прочности на сжатие?

• Гарантированная кубиковая прочность с обеспеченностью 95%.
• Кубиковая прочность бетонных образцов с размером ребра 15 см.
• Временное сопротивление сжатию бетонных кубиков с размерами ребра 15 см, испытанных через 28 суток твердения.
• Временное сопротивление сжатию бетонных кубиков с размерами ребра 15 см, испытанных через 28 суток твердения при температуре 20 ± 2⁰С при нормальном давлении, влажности и с учетом статистической изменчивости прочности.
• Прочность бетонных призм на сжатие.

Что такое железобетонная плита перекрытия, опертая по контуру?

• Плита, работающая на изгиб в двух оротогональных направлениях при соотношении оротогональных сторон опорного контура менее 2, но более 0,5.
• Плита, работающая на изгиб преимущественно в одном направлении при соотношении оротогональных сторон опорного контура более 2 или менее 0,5.
• Плита, опирающаяся на четыре стороны.
• Плита, опирающаяся на три стороны.
• Плита, опирающаяся на две смежные стороны

Что такое железобетон?

• Железобетон – это искусственный строительный материал, представляющий собой рациональное соединение бетона и арматуры, работающих совместно.
• Железобетон – это искусственный строительный материал, представляющий комбинацию, половину из которой составляет литой металл, а другую половину – бетон.
• Железобетон – это искусственный строительный материал, представляющий собой каменную структуру, в которую включены отдельные феритовые зерна.
• Железобетон – это искусственный строительный материал, представляющий комбинированную конструкцию, к которой на растяжение работает сталь, а на сжатие – бетон.
• Железобетон – это искусственный строительный материал, состоящий из шлака и стали, получаемый в результате переплавки руды в домнах или других печах

Что такое бетон?

• Бетон – это искусственный строительный материал, представляющий собой каменную структуру, в которую включены цемент, щебень и вода.
• Бетон – это искусственный строительный материал, представляющий собой рациональное соединение цемента и воды.
• Бетон – это искусственный каменный материал, представляющий комбинацию, половину из которой составляет цемент, а другую половину – песок с водой.
• Бетон – это искусственный каменный материал, который достаточно хорошо сопротивляется сжатию и значительно хуже растяжению.
• Бетон – это искусственный строительный материал, состоящий из шлака и цемента, песка и воды

Что такое балочная железобетонная плита перекрытия?

• Плита, опирающаяся на балки.
• Собранная из отдельных балок.
• Плита, опирающаяся на любые две стороны.
• Плита, работающая на изгиб преимущественно в одном направлении при соотношении оротогональных сторон опорного контура более 2 или менее 0,5.
• Плита, опирающаяся на две противоположные стороны.

Что собой представляет марка раствора?

• Временное сопротивление сжатию в кгс/см2 образца кубика с размером сторон 7,07см испытанного в возрасте 28 дней хранящегося при температуре t=15C при нормальном атмосферном давлении.
• Временное сопротивление сжатию в МПа образца кубика с размером сторон 7,07см испытанного в возрасте 28 дней хранящегося при температуре t=15C при нормальном атмосферном давлении.
• Временное сопротивление сжатию в кгс/см2 образца кубика с размером сторон 10 см испытанного в возрасте 28 дней хранящегося при температуре t=15C при нормальном атмосферном давлении.
• Временное сопротивление сжатию в МПа образца кубика с размером сторон 15 см испытанного в возрасте 28 дней хранящегося при температуре t=15C при нормальном атмосферном давлении.
• Временное сопротивление сжатию в кгс/см2 образца кубика с размером сторон 15 см испытанного в возрасте 28 дней хранящегося при температуре t=15C при нормальном атмосферном давлении.

Что предполагается в континуальных моделях несущей системы многоэтажного здания?

• Заменяется система по методу конечных элементов.
• Сохраняется дискретное расположение вертикальных несущих элементов, а дискретные связи сдвига заменяют непрерывным их распределением по высоте несущей системы.
• Представляет пространственную несущую систему в виде сплошной многостенчатой призматической оболочки с вертикальными или горизонтальными осями.
• Сохраняется дискретное расположение элементов и связей сдвига. Причем элементы системы подвергаются более детальной дискретизации на конечных элементах в методе конечных элементов либо производится замена несущей системы стержневой решеткой в методе замены континуума стержневой решеткой.
• Представляет пространственную несущую систему в виде складчатой оболочки.

Что предполагается в дискретных моделях несущей системы многоэтажного здания?

• Сохраняется дискретное расположение вертикальных несущих элементов, а дискретные связи сдвига заменяют непрерывным их распределением по высоте несущей системы.
• Представляют пространственную несущую систему в виде сплошной многостенчатой призматической оболочки с вертикальными или горизонтальными осями.
• Сохраняется дискретное расположение элементов и связей сдвига. Причем элементы системы подвергаются более детальной дискретизации на конечных элементах в методе конечных элементов либо производится замена несущей системы стержневой решеткой в методе замены континуума стержневой решеткой.
• Заменяется система по методу конечных элементов.
• Представляет пространственную несущую систему в виде складчатой оболочки

Что предполагается вдискретно-континуальных моделях несущей системы многоэтажного здания?

• Представляет пространственную несущую систему в виде складчатой оболочки.
• Сохраняется дискретное расположение вертикальных несущих элементов, а дискретные связи сдвига заменяют непрерывным их распределением по высоте несущей системы.
• Представляют пространственную несущую систему в виде сплошной многостенчатой призматической оболочки с вертикальными или горизонтальными осями.
• Сохраняется дискретное расположение элементов и связей сдвига. Причем элементы системы подвергаются более детальной дискретизации на конечных элементах в методе конечных элементов либо производится замена несущей системы стержневой решеткой в методе замены континуума стержневой решеткой.
• Заменяется система по методу конечных элементов.

Что повышает предварительное напряжение арматуры в центрально растянутых элементах?

• Сцепление арматуры с бетоном.
• Прочность наклонного сечения.
• Трещиностойкость
• Плотность.
• Прочность нормального сечения.

Что означают параметры, фигурирующие в марках сеток – C (D–V)/(d–U) B × L (C₁ C₂)/K?

• С – сетка; D – диаметр поперечных стержней; V – шаг продольных стержней; d – диаметр продольных стержней; U – шаг поперечных стержней; B – длина сетки; L – ширина сетки; C1, C2 – свободные концы поперечных стержней; K – свободные концы продольных стержней.
• С – сетка; D – диаметр продольных стержней; V – шаг продольных стержней; d – диаметр поперечных стержней; U – шаг поперечных стержней; B – ширина сетки; L – длина сетки; C1, C2 – свободные концы продольных стержней; K – свободные концы поперечных стержней.
• С – сетка; D – диаметр поперечных стержней; V – шаг поперечных стержней; d – диаметр продольных стержней; U – шаг продольных стержней; B – длина сетки; L – ширина сетки; C1, C2 – свободные концы поперечных стержней; K – свободные концы продольных стержней.
• С – сетка; D – диаметр поперечных стержней; V – шаг поперечных стержней; d – диаметр продольных стержней; U – шаг продольных стержней; B – длина сетки; L – ширина сетки; C1, C2 – свободные концы продольных стержней; K – свободные концы поперечных стержней.
• С – сетка; D – диаметр поперечных стержней; V – шаг поперечных стержней; d – диаметр продольных стержней; U – шаг продольных стержней; B – длина сетки; L – ширина сетки; C1, C2 – свободные концы продольных стержней; K – свободные концы поперечных стержней.

Чему равен случайный эксцентриситет ea?

• должен приниматься равным 1/600 от длины элемента.
• должен приниматься равным 1/25 от высоты сечения элемента.
• должен приниматься равным 1 см.
• должен приниматься равным 1/30 от высоты сечения элемента.
• должен приниматься равными большему из следующих значений: 1/30 от высоты сечения элемента; 1/600 от длины элемента; 1 см

Чем характеризуется хрупкое разрушение изгибаемых ЖБК?

• σb > Rb; σS > Rs.
• σb = Rb; σS = Rs.
• σb < Rb; σS = Rs.
• σb = Rb; σS < Rs.
• σb < Rb; σS < Rs.

Чем характеризуется пластическое разрушение изгибаемых ЖБК?

• σb > Rb ; σₛ > Rₛ .
• σb > Rb ; σₛ = Rₛ
• σb = Rb ; σₛ = Rₛ .
• σb < Rb ; σₛ < Rₛ .
• σb = Rb ; σₛ < Rₛ .

Чем характеризуется конец первой стадии работы изгибаемых и центрально растянутых элементов?

• σb = Rbt; εb = εbt,u.
• σb = Rb; εb = εb,u.
• σb = Rb; εbt = εbt,u.
• σbt = Rbt; εbt = εbt,u
• σbt = Rbt; εb = εb,u.

Чем отличаются способы обеспечения пространственной жесткости гражданских зданий?

• Способом восприятия вертикальной нагрузки.
• Способом восприятия сейсмической нагрузки.
• Способом восприятия ветровой нагрузки.
• Способом восприятия горизонтальной нагрузки
• Способом устройства фундамента

Чем ограничивается ширина сжатой полки, вводимая в расчет прочности нормального таврового сечения в плитах?

• b`f = 0 – при h`f > 0,1h; b`f = 6h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 12h`f + b – при h`f < 0,05h.
• b`f ≤ l и b`f ≤ l₁/3 + b, где l₁ – расстояние между осями ребер, l – длина элемента. Если толщина полки при этом h`f ≤ 0,1h и отсутствуют поперечные ребра или их шаг больше чем расстояние между продольными ребрами, то b`f = 6h`f + b.
• b`f = 0 – при h`f > 0,1h; b`f = 12h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 6h`f + b – при h`f < 0,05h.
• b`f = 12h`f + b – при h`f > 0,1h; b`f = 6h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 0 – при h`f < 0,05h.
• b`f ≤ l₁ и b`f ≤ l/3 + b, где l₁ – расстояние между осями ребер, l – длина элемента. Если толщина полки при этом h`f ≤ 0,1h и отсутствуют поперечные ребра или их шаг больше чем расстояние между продольными ребрами, то b`f = 12h`f + b

Чем ограничивается ширина сжатой полки, вводимая в расчет прочности нормального таврового сечения в отдельных балках (при консольных свесах)?

• b`f = 0 – при h`f > 0,1h; b`f = 6h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 12h`f + b – при h`f < 0,05h.
• b`f = 12h`f + b – при h`f > 0,1h; b`f = 0 – при 0,1h > h`f ≥ 0,05h; b`f = 6h`f + b – при h`f < 0,05h.
• b`f = 0 – при h`f > 0,1h; b`f = 12h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 6h`f + b – при h`f < 0,05h.
• b`f = 6h`f + b – при h`f > 0,1h; b`f = 12h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 0 – при h`f < 0,05h.
• b`f = 12h`f + b – при h`f > 0,1h; b`f = 6h`f + b – при 0,1h > h`f ≥ 0,05h; b`f = 0 – при h`f < 0,05h

Чем обусловлена совместная работа бетона и арматуры?

• Равенством деформаций в этих материалах
• Равенством поперечных усилий в этих материалах.
• Равенством прочности этих материалов.
• Равенством напряжений в этих материалах.
• Равенством продольных усилий в этих материалах.

Сколько форм свободных колебаний учитывается в общем случае при расчете пространственной несущей системы многоэтажного гражданского здания?

• Четыре.
• Три
• Пять.
• Две.
• Одну.

Сколько стадий работы кладки при сжатии различают?

• Пять.
• Три.
• Четыре
• Одна.
• Две.

При каком условии возникает пространственное деформирование диафрагмовой системы от вертикальной нагрузки?

• При ∑miy · zi + ∑miz · yi ≠ 0 .
• При myeq = ∑miyeq ≠ 0 ; mz eq = ∑miz eq ≠ 0 .
• При miyeq ≠ 0 и miz eq ≠ 0 .
• При ∑miy · zi ≠ 0 ; ∑miz · yi ≠ 0
• При miy · zi ≠ 0 ; miz · yi ≠ 0

При каких напряжениях в сжатой кладке отсутствуют трещины?

• σ < 0,7Ru .
• σ < 0,5Ru
• σ < 0,1Ru .
• σ = Ru .
• σ < 0,9Ru

Поясните геометрический смысл начального модуля упругости бетона?

• Это отношение напряжений к полным деформациям.
• Тангенс угла наклона касательной к диаграмме деформирования в точке соответствующей заданному уровню напряжений σb.
• Это отношение полных деформаций к величине соответствующих напряжений.
• Начальный модуль упругости бетона определяется при напряжениях порядка 0,2 … 0,3 от предела прочности и геометрически представляет собой тангенс угла наклона касательной к диаграмме деформирования на начальном участке
• Тангенс угла наклона секущей на диаграмме деформирования в точке с заданным напряжением.

Почему не рекомендуется назначать слишком большим величину предварительного напряжения?

• Так как может произойти обрыв части арматурных стержней.
• Так как может произойти разрыв проволочной арматуры или развиться усадка бетона.
• Так как может произойти разрыв проволочной арматуры или развитие значительных остаточных деформаций в стержневой. +++
• Так как может произойти разрыв проволочной арматуры или развиться ползучесть бетона.
• Так как может произойти большая релаксация напряжений в арматуре, усадка и ползучесть бетона.

Почему может быть утрачен эффект преднапряжения арматуры при малой величине преднапряжений?

• Из-за разрыва проволочной арматуры или развития значительных остаточных деформаций в стержневой.
• Из-за обрыва части арматурных стержней.
• Из-за разрыва проволочной арматуры или ползучести бетона.
• Вследствие релаксации напряжений в арматуре или развития значительных остаточных деформаций в стержневой арматуре.
• Вследствие релаксации напряжений в арматуре, усадки и ползучести бетона

Под каким номером обозначены на рисунке гибкая связь-подвеска и под каким – гибкая связь-распорка?

• 15 и 16.
• 1 и 5.
• 14 и 15.
• 4 и 18.
• e. 10 и 12.

По какой формуле определить требуемую площадь сечения наклонных стержней, если известна площадь сечения поперечных стержней?

• As,inc = qswS/Rsw , где qsw = RswAsw/S
• As,inc = qswS·sinθ/Rsw , где qsw = RswAsw/S ; θ – угол наклона отгибов.
• As,inc = √Mbqsw /Rswsinθ , где Mb = φb2 (1 + φf + φn) Rbtbh₀² ; qsw = RswAsw/S ; θ – угол наклона отгибов.
• As,inc = (Q – 2√Mbqsw) /Rswsinθ , где Mb = φb2 (1 + φf + φn) Rbtbh₀² ; qsw = RswAsw/S ; θ – угол наклона отгибов.
• As,inc = (Q – 2√Mbqsw) /Rswsinθ , где Mb = φb2 (1 + φf + φn) Rbtbh₀² ; qsw = RswAsw/S ; θ – угол наклона отгибов.

По какой формуле можно первоначально определить площадь подошвы отдельного центрально загруженного железобетонного фундамента под колонну?

• Af = Ncol,n / (R0 – γm Hef), где Ncol,n – продольное усилие в колонне на уровне обреза фундамента от нормативных нагрузок; γm = 20 кН/м³ – усредненная сила тяжести единицы объема фундамента и грунта, находящегося на его обрезах; Hef – глубина заложения фундамента; R0 – условное расчетное сопротивление грунта.
• Af = Ncol / (Rbt – γm Hef), где Ncol – продольное усилие в колонне на уровне обреза фундамента от расчетных нагрузок; γm = 20 кН/м³ – усредненная сила тяжести единицы объема фундамента и грунта, находящегося на его обрезах; Hef – глубина заложения фундамента.
• Af = Ncol / (Rb – γb Hef), где Ncol – продольное усилие в колонне на уровне обреза фундамента от расчетных нагрузок; γb = 25 кН/м³ – усредненная сила тяжести единицы объема тела фундамента; Hef – глубина заложения фундамента.
• Af = Ncol / (R0 – γm Hef), где Ncol – продольное усилие в колонне на уровне обреза фундамента от расчетных нагрузок; γm = 20 кН/м³ – усредненная сила тяжести единицы объема фундамента и грунта, находящегося на его обрезах; Hef – глубина заложения фундамента; R0 – условное расчетное сопротивление грунта.
• Af = Ncol / (Rb – γm Hef), где Ncol – продольное усилие в колонне на уровне обреза фундамента от расчетных нагрузок; γm = 20 кН/м³ – усредненная сила тяжести единицы объема фундамента и грунта, находящегося на его обрезах; Hef – глубина заложения фундамента.

По какой схеме работает каркас здания приведенный на рисунке в поперечном направлении (1 – рамы, 2 – диафрагмы)?

По какой схеме работает каркас здания приведенный на рисунке в продольном направлении (1 – рамы, 2 – диафрагмы)?

• По связевой.
• По диафрагменной.
• По диафрагменной.
• По каркасной.
• По рамной.
• По рамно-связевой.
• По рамной.
• По каркасной.

По какой схеме работает каркас здания приведенный на рисунке в продольном направлении (1 – рамы, 2 – диафрагмы)?

• По рамной.
• По диафрагменной.
• По рамно-связевой.
• По каркасной.
• По связевой.

По каким формулам рассчитывается прочность каменного элемента с продольным армированием при центральном сжатии?

• N ≤ mgφ (0,85RA + RₛAₛ) .
• N ≤ φmg [0,42ωRbh₀² + RₛAₛ(h₀ – a)] / e` .
• N ≤ φmg [0,42ωRbh₀² + RₛA`ₛ(h₀ – a`)] / e ; N ≤ φmg [0,42ωRbh₀² + RₛAₛ(h₀ – a)] / e` .
• N ≤ φmg [0,42ωRbh₀² + RₛA`ₛ(h₀ – a`)] / e .
• N ≤ mgφ (0,85ωRbx + RₛA`ₛ – RₛAₛ)

По каким формулам рассчитывается прочность каменного элемента с продольным армированием при внецентренном сжатии и малых эксцентриситетах при x > 0,55h₀?

• N ≤ φmg [0,42ωRbh₀² + RₛAₛ (h₀ – a)] / e` .
• N ≤ φmg [0,42ωRbh₀² + RₛA`ₛ (h₀ – a`)] / e . N ≤ φmg [0,42ωRbh₀² + RₛAₛ (h₀ – a)] / e` .
• N ≤ mgφ (0,85ωRbx + RₛA`ₛ – RₛAₛ) .
• N ≤ φmg [0,42ωRbh₀² + RₛA`ₛ (h₀ – a`)] / e .
• N ≤ mgφ (0,85RA + RₛAₛ)

По каким формулам рассчитывается прочность каменного элемента с продольным армированием при внецентренном сжатии и больших эксцентриситетах при x ≤ 0,55h0?

1. N ≤ mgφ (0,85RA + RₛAₛ) . нет
2. N ≤ mgφ (0,85ωRbx + RₛA`ₛ – RₛAₛ) .
3. N ≤ φmg [0,42ωRbh₀² + RₛA`ₛ (h₀ – a`)] / e .
4. N ≤ φmg [0,42ωRbh₀² + RₛAₛ (h₀ – a)] / e` . N ≤ φmg [0,42ωRbh₀² + RₛAₛ (h₀ – a)] / e` .
5. N ≤ φmg [0,42ωRbh₀² + RₛA`ₛ (h₀ – a`)] / e .

По каким формулам рассчитывается прочность каменного элемента на срез?

• h₀ = –0,25(hcol + bcol) + 0,5 √Ncol/(Rb+Pef) , где h₀ = –0,25(hcol + bcol) + 0,5 √Ncol/(Rbt+Pef) расчетные сопротивления кладки главным растягивающим напряжениям при изгибе; h₀ = –0,25(hf + bf) + 0,5 √Ncol/(Rb+Pef) ширина сечения; Q = Pef (l₁ – C) bf ≤ плечо внутренней пары сил, для прямоугольного сечения φb3 Rbt bf h₀₁ .
• Q ≤ (Rsq + 0,8nμσ₀) A , где Rsq – расчетное сопротивление срезу; n = 1 – для кладки из сплошного кирпича; n = 0,5– из пустотелого кирпича и камней; μ – коэффициент трения по шву кладки (μ = 0,7– для кирпича); σ₀ = 0,9Nmin/A – сжимающие напряжения в кладке; Nmin – минимальное сжимающее усилие; σb = Mx/Wred расчетная площадь сечения; 0,8 – коэффициент снижения Aₛ – из-за увлажнения и других условий.
• Pef = Ncol,n/Af – ; h₀ = –0,25(hcol + bcol) + 0,5 √Ncol/(Rb+Pef) , где Aₛ = Ncol/Rₛ расчетные сопротивления кладки растяжению по перевязанному шву и главным растягивающим напряжениям при изгибе, соответственно; hcol, bcol – момент упругого сопротивления кладки; h₀ = –0,25(hf + bf) + 0,5 √Ncol/(Rb+Pef) ширина сечения; Q = Pef (l₁ – C) bf ≤ плечо внутренней пары сил, для прямоугольного сечения φb3 Rbt bf h₀₁ .
• Pef = Ntot/Af , где Ntot – расчетное сопротивление кладки осевому растяжению по перевязанному сечению; Aₙ – площадь сечения нетто (за вычетом вертикальных швов).
• Pef = Ncol,n/Af – , где Ncol,n – расчетные сопротивления кладки растяжению по перевязанному шву и главным растягивающим напряжениям при изгибе; hcol, bcol – момент упругого сопротивления кладки.

По каким формулам рассчитывается прочность каменного элемента на растяжение?

• Q ≤ (Rsq + 0,8nμσ₀)A , где Rsq – расчетное сопротивление срезу; n = 1 – для кладки из сплошного кирпича; n = 0,5 – из пустотелого кирпича и камней; μ – коэффициент трения по шву кладки ( μ = 0,7 – для кирпича); σ₀ = 0,9Nmin / A – сжимающие напряжения в кладке; Nmin – минимальное сжимающее усилие; σb = Mx/Wred расчетная площадь сечения; 0,8 – коэффициент снижения Aₛ – из-за увлажнения и других условий.
• h₀ = –0,25(hcol + bcol) + 0,5 √Ncol/(Rb+Pef) , где h₀ = –0,25(hcol + bcol) + 0,5 √Ncol/(Rbt+Pef) расчетные сопротивления кладки главным растягивающим напряжениям при изгибе; h₀ = –0,25(hf + bf) + 0,5 √Ncol/(Rb+Pef) ширина сечения; Q = Pef (l₁ – C) bf ≤ плечо внутренней пары сил, для прямоугольного сечения φb₃ Rbt bf h₀₁ .
• Pef = Ncol,n / Af – ; h₀ = –0,25(hcol + bcol) + 0,5 √Ncol/(Rb+Pef) , где Aₛ = Ncol / Rₛ расчетные сопротивления кладки растяжению по перевязанному шву и главным растягивающим напряжениям при изгибе, соответственно; hcol, bcol – момент упругого сопротивления кладки; h₀ = –0,25(hf + bf) + 0,5 √Ncol/(Rb+Pef) ширина сечения; Q = Pef (l₁ – C) bf ≤ плечо внутренней пары сил, для прямоугольного сечения φb₃ Rbt bf h₀₁ .
• Pef = Ntot / Af , где Ntot – расчетное сопротивление кладки осевому растяжению по перевязанному сечению; Aₙ – площадь сечения нетто (за вычетом вертикальных швов).
• Pef = Ncol,n / Af – , где Ncol,n – расчетные сопротивления кладки растяжению по перевязанному шву и главным растягивающим напряжениям при изгибе; hcol, bcol – момент упругого сопротивления кладки.

По каким формулам рассчитывается прочность каменного элемента на изгиб?

По каким формулам производится расчет по деформациям каменного элемента при внецентренном сжатии?

• N ≤ Eaεu/[A(h – y)e₀/J – 1] .
• N ≤ Eaεu/[A(h – y)e₀/J + 1] .
• M ≤ Ejεu/(h – y) .
• N ≤ γrARtb/[A(h – y)e₀/J – 1] .
• N ≤ Eaεu .

По каким формулам производится расчет на раскрытие трещин каменного элемента при внецентренном сжатии?

• N ≤ Eaεu/[A(h – y)e₀/J + 1] .
• N ≤ Eaεu .
• N ≤ Eaεu/[A(h – y)e₀/J – 1] .
• M ≤ Ejεu/(h – y) .
• N ≤ γrARtb/[A(h – y)e₀/J – 1]

По каким формулам определяются напряжения в бетоне и в продольной арматуре изгибаемых элементов при расчете по методу допускаемых напряжений?

• σb = Mx/Jred ; σₛ = αM(h₀ – x)/Jred ; σ`ₛ = αM(x – a`)/Jred
• σb = Rb ; σₛ = Rₛ ; σ`ₛ = Rsc .
• σb = Mx/Wred ; σₛ = αM(h₀ – x)/Wred ; σ`ₛ = αM(x – a`)/Wred .
• σb = Mx/Jred ; σₛ = Rₛ ; σ`ₛ = Rsc .
• σb = Rb ; σₛ = αM(h₀ – x)/Jred ; σ`ₛ = αM(x – a`)/Jred

По каким формулам можно проверить прочности нормальных сечений внецентренно растянутого ЖБ элемента, если e` > h₀ – a`?

• Ne ≤ A₀Rb bh₀² + RscA`ₛ(h₀ – a`ₛ) + σscA`ₛₚ(h₀ – a`ₚ) ; N = RₛAₛ + γₛ₆RₛₚAₛₚ – Rb bh₀ ξ – RscA`ₛ – σscA`ₛₚ
• Ne ≤ ηRₛₚA`ₛₚ(h`₀ – aₚ) + RₛA`ₛ(h₀ – a`ₛ) ; Ne` = ηRₛₚAₛₚ(h₀ – a`ₚ) + RₛAₛ(h`₀ – aₛ) .
• N = RₛAₛ + γₛ₆RₛₚAₛₚ – Rb bh₀ ξ – RscA`ₛ – σscA`ₛₚ ; N = RₛAₛ + γₛ₆RₛₚAₛₚ – Rb bx – RscA`ₛ – σscA`ₛₚ .
• Ne ≤ ηRₛₚA`ₛₚ(h₀ – a`ₚ) + RₛA`ₛ(h₀ – a`ₛ) ; N = RₛAₛ + γₛ₆RₛₚAₛₚ – Rb bh₀ ξ – RscA`ₛ – σscA`ₛₚ .
• Ne ≤ ηRₛₚAₛₚ(h`₀ – aₚ) + RₛAₛ(h`₀ – aₛ) ; N = RₛAₛ + γₛ₆RₛₚAₛₚ – Rb bx – RscA`ₛ – σscA`ₛₚ

По каким формулам можно проверить прочности нормальных сечений внецентренно растянутого ЖБ элемента, если e` ≤ h₀ – a`?

По каким схеме работают несущие системы многоэтажных бескаркасных зданий?

• По диафрагменной.
• По каркасной.
• По рамной.
• По связевой
• По рамно-связевой.

По каким схемам может произойти разрушение изгибаемых элементов по наклонному сечению?

• а) от действия изгибающего момента обе части элемента,образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сжатой зоны бетона над наклонной трещиной. Трещина раскрывается и развивается по высоте, а сжатая зона уменьшается. Когда напряжения во всей арматуре, пересекаемой трещиной достигнут предельных значений Rs, произойдет разрыв арматуры и разрушение сжатой зоны бетона. Элемент может разрушиться и в том случае, когда напряжения в арматуре меньше Rs, но недостаточна ее анкеровка, что приводит к проскальзыванию арматуры; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует повороту обеих частей элемента, разрушение происходит после достижения предельных напряжений в растянутой зоне бетона и из-за смятия бетона сжатой зоны над наклонной трещиной. Такой характер разрушения вызывается действием главных растягивающих напряжений; в) при малой ширине сечения элемента b состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за раздробления бетона стенки между наклонными трещинами от главных сжимающих напряжений σmc, когда они приблизятся к расчетному сопротивлению бетона на сжатие Rb.
• а) от действия изгибающего момента обе части элемента, образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сжатой зоны бетона над наклонной трещиной. Трещина раскрывается и развивается по высоте, а сжатая зона уменьшается. Когда напряжения во всей арматуре, пересекаемой трещиной достигнут предельных значений Rs, произойдет разрыв арматуры и разрушение сжатой зоны бетона. Элемент может разрушиться и в том случае, когда напряжения в арматуре меньше Rs, но недостаточна ее анкеровка, что приводит к проскальзыванию арматуры; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует повороту обеих частей элемента, разрушение происходит после достижения предельных напряжений в поперечной и наклонной арматуре, пересекающей трещину из-за среза бетона сжатой зоны над наклонной трещиной. Обе части элемента при этом смещаются друг против друга. Такой характер разрушения вызывается действием поперечной силы; в) при малой ширине сечения элемента b состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за раздробления бетона стенки между наклонными трещинами от главных сжимающих напряжений σmc, когда они приблизятся к расчетному сопротивлению бетона на сжатие Rb.
• а) от действия изгибающего момента обе части элемента, образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сжатой зоны. Когда напряжения в растянутой арматуре достигнут предельных значений Rs, произойдет разрыв арматуры и разрушение сжатой зоны бетона; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует по вороту обеих частей элемента, разрушение происходит после достиже ния предельных напряжений в растянутой зоне бетона и из-за смятия бетона сжатой зоны над наклонной трещиной. Такой характер разрушения вызывается действием главных растягивающих напряжений; в) при большой ширине сечения элемента b состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за среза бетона стенки между наклонными трещинами от главных растягивающих напряжений σmt, когда они приблизятся к расчетному сопротивлению бетона на сжатие Rbt.
• а) от действия крутящего момента обе части элемента, образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сечения. Когда напряжения в сжатой зоне бетона достигнут предельных значений Rb, произойдет разрыв арматуры и разрушение сжатой зоны бетона; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует повороту обеих частей элемента, разрушение происходит после достижения предельных напряжений в растянутой зоне бетона и из-за смятия бетона сжатой зоны над наклонной трещиной. Такой характер разрушения вызывается действием главных растягивающих напряжений; в) при большой ширине сечения элемента b состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за среза бетона стенки между наклонными трещинами от главных растягивающих напряжений σmt, когда они приблизятся к расчетному сопротивлению бетона на сжатие Rbt.
• e. а) от действия крутящего момента обе части элемента, образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сечения. Когда напряжения в сжатой зоне бетона достигнут предельных значений Rb, произойдет разрыв арматуры и разрушение сжатой зоны бетона; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует повороту обеих частей элемента, разрушение происходит после достижения предельных напряжений в растянутой зоне бетона и из-за смятия бетона сжатой зоны над наклонной трещиной. Такой характер разрушения вызывается действием главных растягивающих напряжений; в) при малой ширине сечения элемента b состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за раздробления бетона стенки между наклонными трещинами от главных сжимающих напряжений σmc, когда они приблизятся к расчетному сопротивлению бетона на сжатие Rb.

По каким признакам классифицируются бетоны?

• По структуре, по плотности, по виду заполнителя, по типу вяжущего, по назначению, по водонепроницаемости, по морозостойкости
• По структуре, по водонепроницаемости, по морозостойкости, по плотности, по виду заполнителя, по типу вяжущего, по степени упрочнения.
• По структуре, по плотности, по виду заполнителя, по типу вяжущего, по назначению, по зерновому составу, по условиям твердения.
• По структуре, по степени упрочнения, по плотности, по виду заполнителя, по типу вяжущего, по зерновому составу, по условиям твердения.
• По плотности, по виду заполнителя, по типу вяжущего, по назначению, по водонепроницаемости, по морозостойкости, по условиям твердения.

Несущая способность изгибаемых ЖБК при расчете по прочности нормального сечения в общем случае симметричного профиля при ξ ≤ ξR будет обеспечена если выполняется условие?

• Mu ≤ RbtWpl + σyA`s(h₀ – a`).
• Mu ≤ RbAbcZb + RscA`s(h₀ – a`) + σscA`sp(h₀ – a`p).
• Mu ≤ RuWred + σyA`s(h₀ – a`).
• Nu ≤ RbAbc + σyA`s.
• M ≤ RuAbcZb + σyA`s(h₀ – a`).

На каком рисунке приведена конструкция стыка колонны с ригелем со скрытой консолью?

На каком рисунке приведена конструкция стыка колонны с ригелем с открытой консолью?

На каком рисунке приведена конструкция бесконсольного стыка колонны с ригелем?

На каком рисунке изображена ребристая плита с предварительным напряжением арматуры?

На каком рисунке изображена пустотная плита без предварительного напряжения арматуры?

На какой длине устанавливаются поперечные стержни с уменьшенным вдвое шагом в зоне подрезки ригеля связевого каркаса?

• l₁ = 2(Q – RswAsw)/qwl , где Q – поперечная сила у конца подрезки; Asw – площадь дополнительных поперечных стержней, проходящих через угол подрезки.
• l₁ = 2(Q – RswAsw)/qwl + a₀ + 5d , где a₀ – расстояние от оси опоры до конца подрезки; Q – поперечная сила у конца подрезки; Asw – площадь дополнительных поперечных стержней, проходящих через угол подрезки; d – диаметр поперечной арматуры.
• l₁ = 2(Q – RswAsw – RswAs,incSinα)/qwl + a₀ + 5d , где a₀ – расстояние от оси опоры до конца подрезки; α – угол наклона отгибов; Q – поперечная сила у конца подрезки; Asw, As,inc – площадь дополнительных поперечных стержней и отгибов, проходящих через угол подрезки; d – диаметр поперечной арматуры.
• l₁ = Q/qsw , где qsw – погонное усилие в основных поперечных стержнях, установленных с шагом S .
• l₁ = Q/qsw + S , где S – основной шаг поперечных стержней вне подрезки; qsw – погонное усилие в основных поперечных стержнях, установленных с шагом S .

Кубиковая прочность какого кубика выше?

• С размером ребра 20 см.
• С размером ребра 25 см.
• С размером ребра 30 см.
• С размером ребра 15 см.
• С размером ребра 10 см

Когда эксцентриситет e₀ приложения сжимающей продольной силы во внецентренно сжатых ЖБК считается малым?

• При ξ > ξR .
• При ξ ≤ ξR .
• При e₀ <0,5h₀ .
• При e₀ < h₀ .

Когда эксцентриситет e₀ приложения сжимающей продольной силы во внецентренно сжатых ЖБК считается большим?

• При ξ ≤ ξR .
• При e₀ <0,5h₀ .
• При ξ > ξR .
• При e₀ < h .
• При e₀ < e₀,min

Когда происходят первые и вторые потери предварительного напряжения арматуры?

• Первые потери предварительного напряжения в арматуре происходят в первые сутки после бетонирования, а вторые потери происходят через месяц после бетонирования.
• Первые потери предварительного напряжения в арматуре происходят при изготовлении элемента и обжатии бетона, а вторые потери происходят после обжатия бетона.
• Первые потери предварительного напряжения в арматуре происходят до бетонирования ЖБК, а вторые потери происходят при обжатии бетона.
• Первые потери предварительного напряжения в арматуре происходят после обжатия бетона, а вторые потери происходят при изготовлении элемента и обжатии бетона.
• Первые потери предварительного напряжения в арматуре происходят в течение первого месяца после бетонирования, а вторые потери происходят через год после загружения эксплуатационной нагрузкой.

Какой цифрой обозначена арматура класса А-II, а какой Вр-I ?

• 2 и 3.
• 3 и 4.
• 2 и 4
• 1 и 4.
• 1 и 3.

Какой фигурой представляется эпюра ветровой нагрузки, вводимая в расчет?

• Трапецией.
• Фигурой, ограниченной с одной стороны ломаной линией
• Ромбом.
• Сосредоточенными силами.
• Прямоугольником.

Какой размер ребра кубика принят для эталона кубиковой прочности?

• 10 см
• 15 см
• 25 см
• 20 см
• 7,07 см

Какой максимальный шаг вертикальных арматурных каркасов допускается при армировании железобетонных диафрагм?

• 400 мм
• 3000 мм.
• 1500 мм.
• 200 мм.
• 500 мм.

Какой максимальный шаг вертикальных арматурных каркасов допускается при армировании бетонных диафрагм?

• 3000 мм.
• 200 мм.
• 400 мм.
• 1500 мм
• 500 мм.

Какой величины назначается минимальная величина передаточной прочности?

• Rbp принимают не менее 25 Мпа.
• Rbp принимают не менее 0,6Rb, а при наличии арматуры классов Ат-VI, К7, К19 – не менее 0,8Rb.
• Rbp принимают не менее 0,5Rb, а при наличии арматуры классов Ат-VI, К7, К19 – не менее 0,7Rb.
• Rbp принимают не менее 11 Мпа, а при наличии арматуры классов Ат-VI, К7, К19 – не менее 15,5 Мпа.
• Rbp принимают не менее 20 Мпа.

Какой величины назначается защитный слой бетона фундамента?

• aзс = 50 мм.
• aзс = 70 мм.
• при наличии бетонной подготовки aзс = 70 мм, а при ее отсутствии – aзс = 35 мм.
• при наличии бетонной подготовки aзс = 35 мм, а при ее отсутствии – aзс = 70 мм.
• aзс = 35 мм

Какое эквивалентное поперечное сечение принимается при расчете ребристых плит перекрытия с ребрами, направленными вверх?

• Тавровое с полкой в сжатой зоне.
• Двутавровое.
• Тавровое с полкой в растянутой зоне
• Квадратное.
• Прямоугольное.

Какое эквивалентное поперечное сечение принимается при расчете пустотных плит?

• Прямоугольное.
• Двутавровое
• Тавровое с полкой в сжатой зоне.
• Тавровое с полкой в растянутой зоне.
• Квадратное.

Какое условие прочности используется при расчете прочности центрально сжатых неармированных каменных элементов?

• Ncol,n – , где Rbt = Rbtnγbt. ; e0g – эксцентриситет длительных нагрузок; Ac – площадь сжатой части сечения, у которой центр тяжести совпадает с точкой приложения внешней силы N в предположении прямоугольной эпюры напряжений, для прямоугольного сечения имеем Ac = bchc = A(1 – 2e₀/h) , здесь A = bh – площадь всего сечения; φ₁ – коэффициент продольного изгиба, определяемый как среднее арифметическое между коэффициентом продольного изгиба φ для всего сечения высотой h и коэффициентом продольного изгиба φc для сжатой части сечения элемента, высота которой для прямоугольного сечения hc = h – 2e₀; φ₁ = (φ+φc)/2 . При этом φc определяется по гибкости сжатой части αзc = Af = Ncol/(Rb – γₘHef) , где Ncol – радиус инерции сжатой части.
• σ`ₛ = αM(x – a`)/Jred , где N – расчетная продольная сила; σb = Mx/Wred площадь поперечного сечения; σₛ = αM(h₀ – x)/Wred расчетное сопротивление кладки сжатию; σ`ₛ = αM(x – a`)/Wred коэффициент продольного изгиба, зависящий от упругой характеристики кладки α и гибкости элемента λh или λi, определяемый по таблице СниП (φ<1) ; mg – коэффициент снижения несущей способности кладки изза ползучести при длительном загружении: mg = 1 – ηNg/N , здесь η – коэффициент, учитывающий вид кладки и гибкости элемента, принимаемый по СниП (η<0,4) ; Ng – расчетная продольная сила от длительных нагрузок
• σ`ₛ = αM(x – a`)/Jred , где N – расчетная продольная сила; σb = Mx/Wred площадь поперечного сечения; σₛ = αM(h₀ – x)/Wred расчетное сопротивление кладки сжатию; σ`ₛ = αM(x – a`)/Wred коэффициент продольного изгиба, зависящий от упругой характеристики кладки α и гибкости элемента λh или λi, определяемый по таблице СниП (φ<1) ; mg – коэффициент снижения несущей способности кладки из-за ползучести при длительном загружении: mg = 1 – ηNg/N , здесь η – коэффициент продольного изгиба η = 1/(1 – N/Ncr) ; Ng – расчетная продольная сила от длительных нагрузок.
• N ≤ mgφ₁RAcω , где Rbt = Rbtnγbt. ; e0g – эксцентриситет длительных нагрузок; Ac – площадь сжатой части сечения, у которой центр тяжести совпадает с точкой приложения внешней силы N в предположении прямоугольной эпюры напряжений, для прямоугольного сечения имеем Ac = bchc = A(1 – 2e₀/h) , здесь A = bh – площадь всего сечения; φ₁ – коэффициент продольного изгиба, определяемый как среднее арифметическое между коэффициентом продольного изгиба φ для всего сечения высотой h и коэффициентом продольного изгиба φc для сжатой части сечения элемента, высота которой для прямоугольного сечения hc = h – 2e₀; φ₁ = (φ+φc)/2 . При этом φc определяется по гибкости сжатой части αзc = Af = Ncol/(Rb – γₘHef) , где Ncol – радиус инерции сжатой части; γₘ = 20 , а для сечений произвольной формы Hef – , где Af = Ncol/(R₀ – γₘHef) расстояние до центра тяжести сечения, которое при R₀ – принимают из условия Af = Ncol,n/(R₀ – γₘHef) .
• σ`ₛ = αM(x – a`)/Jred , где N – расчетная продольная сила; σb = Mx/Wred площадь поперечного сечения; σₛ = αM(h₀ – x)/Wred расчетное сопротивление кладки сжатию; σ`ₛ = αM(x – a`)/Wred коэффициент продольного изгиба, зависящий от расчетного сопротивления кладки σb = Rb и расчетной длины элемента, определяемый по таблице СниП (φ<1); mg – коэффициент снижения несущей способности кладки изза ползучести при длительном загружении: mg = 1 – ηNg/N , здесь η – коэффициент, учитывающий вид кладки и гибкости элемента, принимаемый по СниП (η<0,4); Ng - расчетная сила от длительных нагрузок

Какое условие прочности используется при расчете прочности внецентренно сжатых неармированных каменных элементов?
Выберите один ответ:

• σ`ₛ = αM(x – a`)/Jred , где N – расчетная продольная сила; σb = Mx/Wred площадь поперечного сечения; σₛ = αM(h₀ – x)/Wred расчетное сопротивление кладки сжатию; σ`ₛ = αM(x – a`)/Wred коэффициент продольного изгиба, зависящий от расчетного сопротивления кладки σb = Rb и расчетной длины элемента, определяемый по таблице СниП (φ<1); mg – коэффициент снижения несущей способности кладки изза ползучести при длительном загружении: mg = 1 – ηNg/N , здесь η – коэффициент, учитывающий вид кладки и гибкости элемента, принимаемый по СниП (η<0,4); Ng – расчетная продольная сила от длительных нагрузок.
• σ`ₛ = αM(x – a`)/Jred , где N – расчетная продольная сила; σb = Mx/Wred площадь поперечного сечения; σₛ = αM(h₀ – x)/Wred расчетное сопротивление кладки сжатию; σ`ₛ = αM(x – a`)/Wred коэффициент продольного изгиба, зависящий от упругой характеристики кладки α и гибкости элемента λh или λi, определяемый по таблице СниП (φ<1) ; mg – коэффициент снижения несущей способности кладки из-за ползучести при длительном загружении: mg = 1 – ηNg/N , здесь η – коэффициент продольного изгиба η = 1/(1 – N/Ncr) ; Ng – расчетная продольная сила от длительных нагрузок.
• Ncol,n – , где Rbt = Rbtnγbt. ; e0g – эксцентриситет длительных нагрузок; Ac – площадь сжатой части сечения, у которой центр тяжести совпадает с точкой приложения внешней силы N в предположении прямоугольной эпюры напряжений, для прямоугольного сечения имеем Ac = bchc = A(1 – 2e₀/h) , здесь A = bh – площадь всего сечения; φ₁ – коэффициент продольного изгиба, определяемый как среднее арифметическое между коэффициентом продольного изгиба φ для всего сечения высотой h и коэффициентом продольного изгиба φc для сжатой части сечения элемента, высота которой для прямоугольного сечения hc = h – 2e₀; φ₁ = (φ+φc)/2 . При этом φc определяется по гибкости сжатой части αзc = Af = Ncol/(Rb – γₘHef) , где Ncol – радиус инерции сжатой части.
• N ≤ mgφ₁RAcω , где Rbt = Rbtnγbt. ; e0g – эксцентриситет длительных нагрузок; Ac – площадь сжатой части сечения, у которой центр тяжести совпадает с точкой приложения внешней силы N в предположении прямоугольной эпюры напряжений, для прямоугольного сечения имеем Ac = bchc = A(1 – 2e₀/h) , здесь A = bh – площадь всего сечения; φ₁ – коэффициент продольного изгиба, определяемый как среднее арифметическое между коэффициентом продольного изгиба φ для всего сечения высотой h и коэффициентом продольного изгиба φc для сжатой части сечения элемента, высота которой для прямоугольного сечения hc = h – 2e₀; φ₁ = (φ+φc)/2 . При этом φc определяется по гибкости сжатой части αзc = Af = Ncol/(Rb – γₘHef) , где Ncol – радиус инерции сжатой части; γₘ = 20 , а для сечений произвольной формы Hef – , где Af = Ncol/(R₀ – γₘHef) расстояние до центра тяжести сечения, которое при R₀ – принимают из условия Af = Ncol,n/(R₀ – γₘHef) .
• σ`ₛ = αM(x – a`)/Jred , где N – расчетная продольная сила; σb = Mx/Wred площадь поперечного сечения; σₛ = αM(h₀ – x)/Wred расчетное сопротивление кладки сжатию; σ`ₛ = αM(x – a`)/Wred коэффициент продольного изгиба, зависящий от упругой характеристики кладки α и гибкости элемента λh или λi, определяемый по таблице СниП (φ<1) ; mg – коэффициент снижения несущей способности кладки из-за ползучести при длительном загружении: mg = 1 – ηNg/N , здесь η – коэффициент, учитывающий вид кладки и гибкости элемента, принимаемый по СниП (η<0,4) ; Ng – расчетная продольная сила от длительных нагрузок.

Какое условие прочности используется при расчете внецентренно сжатого ЖБ элемента?

• Ne ≤ Rb bξR h₀ + RscA`ₛ(h₀ – a`) .
• Ne ≤ AR Rb bh₀² + RscA`ₛ(h₀ – a`) .
• Ne ≤ Rb bξR h₀ + RscA`ₛ .
• N ≤ Rb bx + RscA`ₛ .
• Ne ≤ Rb bx (h₀ – 0,5x) + RscA`ₛ(h₀ – a`)