Методы расчета напряженно-деформированного состояния вагонных конструкций

1. Методы расчета напряженно-деформированного состояния вагонных конструкций

В соответствии с действующими нормами проектирования вагонов напряжения и перемещения в элементах конструкции вагона должны определяться современными методами сопротивления материалов, теории упругости и строительной механики.

Длительный опыт создания вагонов определил целый ряд подходов к расчету их несущих элементов. Одним из таких подходов является использование метода сил. До появления ЭВМ этот метод, в силу меньшей трудоемкости по сравнению с методом перемещений, был основным при расчете большей части вагонных конструкций. С появлением ЭВМ стала широко использоваться матричная форма метода сил.

 Развитие вычислительной техники в направлении увеличения мощности ЭВМ и их быстродействия обусловили широкое внедрение в расчетную практику численных методов. Одним из наиболее эффективных является метод конечных элементов (МКЭ). Нормами проектирования этот метод рекомендуется в качестве основного при расчете напряженно-деформированного состояния узлов и деталей вагонов.

Расчетные схемы различных элементов вагонных конструкций могут быть сведены к стержневым, пластинчатым, оболочечным, объемным или комбинированным системам, находящимся под действием различных наг­рузок. В настоящее время для их расчета на прочность используется программные комплексы, реализующие МКЭ. В частности нормами проектирования вагонов рекомендуется использование пакетов прикладных программ «Прочность», «Спринт», «Лира» и др. Эти комплексы обеспечивает контроль подготовки исходных данных, численную машинную реализацию алгоритмов расчета конструкций, выдачу результатов в удобней для практического использования форме.

Для расчета напряженно-деформированного состояния элементов вагонов в виде пластин (например, панель обшивки) и оболочек (например, цилиндрическая оболочка котла цистерны) используются методы теории упругости. Решение уравнений теории упругости производится (в большинстве случаев) численными методами, наибольшее распространение при этом получил метод сеток.

Изложенное выше относится к статическим расчетам напряженно-деформированного состояния деталей и узлов вагонов. При движении вагона в поезде кузов, рамы тележек и другие детали испытывают вибрации, вызванные упругими деформациями материала под действием динамических сил со стороны рессор и автосцепного оборудования. Импульсные и периодические нагрузки воздействуют на вагоны при погрузке навалочных грузов, разгрузке их с помощью вибромашин, при маневровых соударениях, при проходе колесом рельсового стыка, стрелочного перевода и других неровностей железнодорожного пути. Упругие вибрации вызывают дополнительные (к статическим) напряжения в конструкциях, которые приводят к появлению усталостных повреждений. При проектировании вагонов необходимо давать оценку прочности элементов конструкции с учетом вибрационного нагружения. Решение этой задачи осуществляется на ЭВМ на основе интегрирования дифференциальных уравнений движения упругих систем с использованием численных методов.

1.1. МАТРИЧНАЯ ФОРМА МЕТОДА СИЛ ПРИМЕНИТЕЛЬНО К РАСЧЕТУ ПРОСТРАНСТВЕННЫХ ВАГОННЫХ КОНСТРУКЦИЙ

Метод сил используется для расчета напряженного состояния стержневых статически неопределимых систем (систем, для которых уравнений равновесия (статики) недостаточно для определения усилий в отдельных элементах расчетной схемы).

Рекомендуемые материалы

Основной идеей метода является переход от статически неопределимой расчетной схемы к статически определимой основной системе, которая получается путем отбрасывания «лишних» связей и введения разрезов. Основная система эквивалентна расчетной схеме за счет введения сил и моментов (реакций) в местах разрезов и отброшенных связей. Указанные усилия обеспечивают отсутствие перемещений в направлении отброшенных связей и в местах мнимых разрезов.

Силы и моменты в местах разрезов и отброшенных связей неизвестны. Их значения, обеспечивающие отсутствие указанных выше перемещений, находятся из равенства перемещений от этих усилий и перемещений от внешних нагрузок. Математически это условие представляет собой систему канонических уравнений метода сил. Решая эту систему находят неизвестные ранее усилия, которые обеспечивают эквивалентность основной системы расчетной схеме.

Общая процедура метода сил в обычной форме включает следующие операции:

- определяется степень статической неопределимости расчетной схемы. Степень статической неопределимости при решении пространственных задач n=6k – Ш, где k – количество замкнутых контуров, а Ш – количество шарниров, несвязанных с землей;

- выбирается основная система путем отбрасывания «лишних» связей и (или) введения разрезов. В местах отброшенных связей и разрезов вводятся неизвестные усилия Х_i (силы и (или) моменты), делающие основную систему эквивалентной расчетной схеме. Основное требование при этом – основная система должна быть кинематически неизменяема;

- строятся единичные эпюры в основной системе от Х_i = 1 (i=1...n);

- строится грузовая эпюра (тоже в основной статически определимой системе);

- записывается система канонических уравнений метода сил в виде

                                     

     (1.1)

где δ_ij – коэффициенты при неизвестных усилиях, представляющий  перемещение по направлению i , вызванное силой, равной единице, действующей по направлению j;

Δ_ip – перемещение по i –тому направлению от нагрузок в основной системе;

- путем перемножения соответствующих эпюр рассчитываются коэффициенты δ_ij и Δ_ip;

- производится проверка правильности вычисления коэффициентов δ_ij и Δ_ip;

- решается система канонических уравнений (1.1) и находятся ранее неизвестные усилия (реакции) Х_i;

- путем умножения единичных эпюр на найденные значения Х_i  строятся исправленные эпюры;

- суммированием исправленных эпюр и грузовой строятся расчетные эпюры внутренних усилий (изгибающих, крутящих моментов, нормальных усилий);

- производится деформационная проверка;

- анализируются эпюры внутренних усилий, выявляются наиболее опасные сечения и рассчитываются напряжения в расчетных точках сечений.

При расчете коэффициентов δ_ij и Δ_ip обычно учитываются только деформации изгиба, так как другие виды деформации считаются несущественными. Расчетные эпюры поперечных и нормальных сил строятся по полученным расчетным эпюрам изгибающих моментов. Такой подход имеет место при расчете по методу сил большинства строительных конструкций. При расчете пространственных вагонных конструкций приходится учитывать (в силу их существенности) деформации изгиба в двух плоскостях (в вертикальной и горизонтальной), кручения и растяжения-сжатия. Не учитываются только деформации сдвига, так как их учет существенно усложняет расчет, а повышение точности при этом составляет около 2 %.

Расчет напряженного состояния конструкций по методу сил в обычной его форме является весьма трудоемким, так как использование ЭВМ возможно только для выполнения отдельных процедур, но не для расчета в целом.  Более формализованной, и поэтому более приспособленной для программирования, является матричная форма этого метода.

Система канонических уравнений в матричной форме имеет вид

                                              

DX + Δ = 0,           (1.2)

где   D - матрица  коэффициентов уравнений  перемещений  от единичных

силовых факторов;

X — матрица неизвестных метода сил;

Δ — матрица грузовых (свободных) членов - перемещений от нагрузок.

Как следует из сравнения этой формулы с ранее принятым выражением вида (1.1), коэффициенты при неизвестных образуют квадратную мат­рицу порядка п:

                          

а неизвестные и грузовые члены - прямоугольные матрицы размера (п X а). Здесь а - число одновременно рассчитываемых независимых схем нагружения. Эти схемы нагружения обус­ловлены желанием оценить напряженное состояние рассчитываемой  конструкции от действия различных нагрузок (например, вертикальной и горизонтальной).

Если обозначить индексами в и г соответственно вертикальные и гори­зонтальные нагрузки, то

 

                            

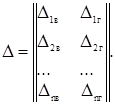
В этих матрицах для упрощения второй индекс вместо общепринятого номера столбца заменен индексом нагрузки.

Вычисляя коэффициенты и грузовые члены без учета деформаций сдви­га, можно представить их в виде матрицы

              A = L^T_y·F_y·T_y + L^т_z·F_z·T_z + L^т_x·F_x·T_x + L^т_N·F_N·T_N = .   (1.3)

Здесь L^T - матрица, транспонированная к L, т. е. строки матрицы L^T яв­ляются столбцами матрицы L, L_y, L_z, L_x и L_N - матрицы внутренних сил в основной системе от единичных неизвестных, составленные из ординат единичных эпюр моментов соответственно М_у (изгибающих моментов в вертикальной плоскости), М_z (изгибающих моментов в горизонтальной плоскости), М_х (крутящих моментов) и нормальной силы N. Эти матрицы имеют размер (т X a), где т - число сечений рамы, в ко­торых определяются внутренние силовые факторы.

В отличии от обычной формы метода сил, при использовании матричной формы после выбора основной системы расчетная схема разбивается на участки, ограниченные с каждой из сторон расчетными сечениями. Признаками разбиения на участки являются: изменение жесткости стержней, размещение нагрузок (сосредоточенных сил и моментов, распределенных нагрузок – с тем, чтобы в пределах участка не было эпюр с переломами и скачками внутренних усилий).

В первом столбце каждой из матриц L приведены ор­динаты эпюр силовых факторов во всех т сечениях от неизвестного Х₁=1, во втором - от Х₂ = 1 и т. д.

Если грузовые эпюры представить в виде аналогичных матриц L_Py , L_Pz , L_Px , L_Pn  размера (m X а) и объединить с соответствующими матри­цами L_y, L_z, L_x и L_N то получим расширенные матрицы Т_у, Т_z, Т_x и T_N размера [т X (п + а)]. Например, матрица T_z состоит из матрицы L_z и приписанной с обратным знаком матрицы L_Pz, т. е. .

Информация о геометрических параметрах расчетной схемы (длины уча­стков, моменты инерции и площади сечений и т. п.) содержится в виде мат­риц податливостей элементов системы F_y (при изгибе в вертикальной плоскости), F_z (при изгибе в горизонтальной плоскости), F_x (при кручении) и F_N (при растяжении-сжатии). Эти матрицы для рас­сматриваемой задачи являются квазидиагональными с числом блоков, рав­ным числу участков ( это число равно т/2), и размером (т X т).

Если в такой матрице показать только блоки, отличные от нуля, остав­ляя вместо нулей пустые места, то получим (например, для матрицы податливости при изгибе в горизонтальной плоскости)

                                 

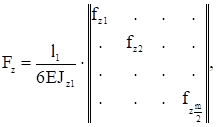
где   - податливость первого элемента, представленная в виде множителя, чтобы элементы матрицы f_zi имели безразмерную ве­личину;

l₁ – длина первого участка;

Е – модуль упругости;

J_z1 – момент инерции сечения стержня первого участка при изгибе в горизонтальной плоскости.

                                           

- коэффициент при блоке   , представляющем матричную форму перемножения эпюр (трапеции на трапецию).

В этом выражении l_i – длина i – того участка;

J_z1 – момент инерции сечения стержня  i – того участка при изгибе в горизонтальной плоскости.

Матрицы податливости элементов системы F_y, F_x и F_N могут быть получены из матрицы F_z путем замены коэффициентов k_zi при блоках на коэффициенты соответственно

                        

          и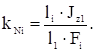  

Где J_yi – момент инерции сечения стержня  i – того участка при изгибе в вертикальной плоскости;

       J_xi – момент инерции сечения стержня  i – того участка при кручении.

               F_i – площадь сечения i – того участка;

               G – модуль упругости при кручении и сдвиге.

Выражение (1.3) представляет собой матричный алгоритм вычис­ления коэффициентов и грузовых членов канонических уравнений метода сил, учитывающий деформации изгиба в вертикальной плоскости (первое слагаемое), изгиб в горизонтальной плоскости (второе слагаемое), кручение (третье слагаемое) и растяжение-сжатие (четвертое слагаемое). Вертикальная черта после матрицы D означает, что к ней приписывается с обратным знаком матрица Δ.

После формирования матриц, входящих в выражение (1.3), решается система урав­нений (1.2), т. е. определяются неизвестные X = - D^-1·Δ, а по ним вычисляются ординаты расчетных эпюр силовых факторов в рассчитываемой статически неопределимой системе. Эти ординаты получаются в виде матриц размера (т Х а):

                                                               (1.4)

Выражения (1.4.) в матричной форме реализуют процедуры определения ординат исправленных эпюр и получения ординат расчетных эпюр внутренних усилий путем суммирования исправленных эпюр и грузовых.

При расчете можно просто осуществить деформационную проверку, кон­тролирующую правильность всех выполняемых машиной вычислений. В матричной форме эта проверка, отражающая отсутствие в основной системе взаимных перемещений по направлению связей, удаляемых в основной системе, имеет вид

                        L^T_y·F_y·S_y + L^T_z·F_z·S_z + L^T_x·F_x·S_x + L^T_N·F_N·S_N = 0.         (1.5)

1.1.1. ПРИМЕР РАСЧЕТА ПРОСТРАНСТВЕННЫХ КОНСТРУКЦИЙ С ИСПОЛЬЗОВАНИЕМ МАТРИЧНОЙ ФОРМЫ МЕТОДА СИЛ

На рис. 1.1,а приведена простейшая расчетная схема пространственной системы состоящей из двух жестко соединенных стержней АВ и ВС, изготовленных из  стали и имеющих различные размеры поперечных сечений. Левый конец балки «А» жестко заделан, а правый «С» опирается на опоры, запрещающие перемещения правого концевого сечения в вертикальном (по оси Z) и в горизонтальном (по оси Y) направлениях. В месте соединения стержней (в точке В) приложены сосредоточенные силы Р_х, Р_y, P_z и крутящий (относительно оси Х) момент М_х. Индекс в обозначениях сил обозначают  оси координат, в направлении которых они действуют, а в обозначении моментов – оси, относительно которых происходит поворот.

Перед расчетом по методу сил необходимо определить геометрические характеристики сечений стержней – моменты инерции при изгибе в вертикальной и горизонтальной плоскостях, моменты инерции при кручении и площади сечений.

Моменты инерции при изгибе в вертикальной плоскости стержней АВ и ВС соответственно

         

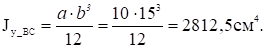
Моменты инерции при изгибе в горизонтальной плоскости стержней АВ и ВС соответственно

         

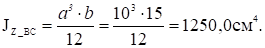
Момент инерции при кручении прямоугольного сечения при b>a J_x =α·a⁴, где α – коэффициент, зависящий от соотношения сторон b/a прямоугольника и принимаемый по табл. 1.1.

Таблица 1.1.

Значения коэффициента α

Для стержня АВ b/a=20/10=2. α =0,457. J_{x_AB}=0,457·10⁴ =4570 см⁴.

Для стержня ВС b/a=15/10=1,5. α =0,294. J_{x_AB}=0,294·10⁴ =2940 см⁴.

Расчетная схема в рассматриваемом примере является два раза статически неопределимой, так как подвижная опора на правом конце ограничивает только

две степени свободы – линейные перемещения по направлениям осей Z и Y. Таким образом в рассматриваемом случае n=2.

На рис. 1.1.,б приведена принятая основная система, в которой отброшенные связи заменены неизвестными силами (реакциями) Х₁ и Х₂. Следует отметить, что отбрасываемые связи, ограничивающие линейные перемещения (это стержни, соединенные с землей) заменяются силами, направленными вдоль этих стержней, а связи, ограничивающие повороты (к ним относятся плавающие заделки), заменяются неизвестными моментами, действующими относительно тех осей, относительно которых ограничивают поворот плавающие заделки.

На этом же рисунке приведена разбивка на участки и приведены расчетные сечения. Номера участков помещены в квадратики, а номера расчетных сечений – в кружки. Как следует из рисунка, нумерация участков и расчетных сечений ведется со стороны отброшенных связей. Каждый участок ограничен расчетными сечениями, принадлежащими только ему. Расчетные сечения под номерами 2 и 3 располагаются на бесконечно малом расстоянии друг от друга. Таким образом стержень ВС представлен участком №1 с расчетными сечениями №1 и №2, а стержень АВ – участком №2 с сечениями №3 и №4, то есть в рассматриваемом случае m=4. Как отмечалось ранее, разбивка расчетной схемы на участки обусловлена наличием в конструкции стержней разной жесткости, а также местом и видом приложенной нагрузки – так, чтобы при построении эпюр внутренних усилий в пределах участка не было переломов и скачков.

На рис. 1.1.,в приведены единичные эпюры, построенные в основной системе. Сила Х₁=1 изгибает балку в вертикальной плоскости, а сила Х₂=1 – в горизонтальной  плоскости.

По полученным эпюрам строятся матрицы Li размером (m x n), составленные из ординат единичных эпюр (i – вид деформации). Первый столбец этих матриц включает в себя ординаты единичных эпюр от Х₁, а второй – от Х₂. Значения ординат эпюр в столбцах располагаются в порядке возрастания номеров расчетных сечений.

                                 

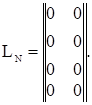
Матрица L_y состоит из ординат эпюр изгибающих моментов, действующих в вертикальной плоскости. Значения элементов второго столбца равны нулю, так как сила Х₂ не вызывает изгиба элементов рассматриваемой основной системы в вертикальной плоскости – т.е. эпюра M_y  от Х₂=1 отсутствует. Правило знаков ординат эпюр изложено ниже при формировании грузовых векторов.

Матрица L_z состоит из ординат эпюр изгибающих моментов, действующих в горизонтальной плоскости. Значения элементов первого столбца равны нулю, так как сила Х₁ не вызывает изгиба элементов рассматриваемой основной системы в горизонтальной  плоскости – т.е. эпюра M_z  от Х₁=1 отсутствует.

Матрицы L_x и L_N содержат нулевые столбцы, так как силы Х₁ и Х₂ не вызывают деформаций кручения  и растяжения-сжатия стержня основной системы. Следовательно, применительно к рассматриваемому примеру, в выражении (1.3) третье и четвертое слагаемые равны нулю – т.е.

                                  

A = L^T_y·F_y·T_y + L^т_z·F_z·T_z = .   (1.6)

Физически это означает, что перемещения в рассматриваемом примере обусловлены только деформациями изгиба стержня в вертикальной и горизонтальной плоскостях.

На рис. 1.1.,г приведены грузовые эпюры, построенные в основной системе. Нагрузки, приложенные к рассматриваемому стержню, вызывают деформации изгиба в вертикальной и горизонтальной плоскостях, кручение и сжатие. Касательные напряжения при кручении стержня и нормальные напряжения при его сжатии могут быть сразу определены по построенным грузовым эпюрам, так как в отношении указанных деформаций рассматриваемая система является статически определимой и эти виды деформаций не зависят от других видов деформаций. По построенным эпюрам формируются матрицы L_Pi размером (m x a), элементами которых являются ординаты грузовых эпюр, записанные в столбец в порядке возрастания номеров расчетных сечений. В рассматриваемом случае а=1 (имеет место один вариант нагружения).

                    

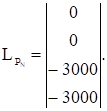
Вектор-столбец L_Рy составлен из ординат эпюры изгибающих моментов, действующих в вертикальной плоскости; L_РZ - из ординат эпюры изгибающих моментов, действующих в горизонтальной плоскости; L_Рx - из ординат эпюры крутящих моментов, действующих в относительно оси Х; L_РN - из ординат эпюры нормальных усилий, действующих вдоль стержня. Векторы-столбцы L_Рx и L_РN для решения рассматриваемой задачи не нужны и приведены только в качестве примера формирования этих векторов. При формировании приведенных выше векторов необходимо обращать внимание на знаки ординат эпюр. Эпюры изгибающих моментов  строятся со стороны растянутых волокон. Рекомендуется следующее правило знаков:

- при изгибе в вертикальной плоскости – знак «-», если эпюра располагается над стержнем (растянуты верхние волокна) и знак «+» - если растянуты нижние волокна;

- при изгибе в горизонтальной плоскости – знак «-», если эпюра располагается перед стержнем (растянуты волокна, обращенные наружу) и знак «+» - если растянуты волокна с обратной стороны;

- при растяжении-сжатии – знак «+», если волокна растянуты и «-», если они сжаты;

- при кручении – «+» - при кручении по часовой стрелке со стороны отброшенных связей, и «-» - при кручении против часовой стрелки.

Следующим этапом реализации матричной формы метода сил является формирование матриц податливости для различных видов деформаций. Как отмечалось выше, в рассматриваемом примере коэффициенты канонических уравнений зависят только от деформаций изгиба в двух плоскостях – в вертикальной и горизонтальной. В связи с этим требуется формирование матриц F_y и F_z.

Как отмечалось в разделе 1.1, для получение удобных для расчета значений матриц податливостей, податливость первого участка рекомендуется выносить за матрицы.

Матрица податливости F_y , содержащая податливость стержней при изгибе в вертикальной плоскости имеет вид

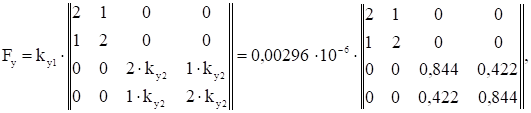
где k_y1 =l_ВС /(6EJ_{y_BC})=100/(6·2812,5·2·10⁶)=0,00296·10⁶;

 k_y2 =[l_AB /(6EJ_{y_AB})]/k_y1=[100/(6·6666,67·2·10⁶)]/k_y1=0,422.

Если бы матрица F_y в примере отсутствовала, податливость первого участка можно было вынести из любой другой имеющейся матрицы.

Матрица податливости F_z , содержащая податливость стержней при изгибе в горизонтальной плоскости имеет вид

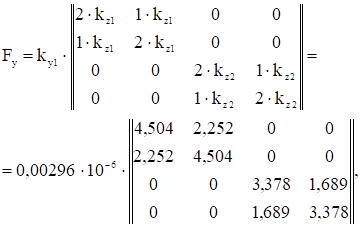
где k_z1 =[l_ВС /(6EJ_{z_BC})]/k_y1=[100/(6·1250,0·2·10⁶)]/ 0,00296·10^-6=2,252;

 k_z2 =[l_AB /(6EJ_{z_AB})]/k_y1=[100/(6·6666,67·2·10⁶)]/ 0,00296·10^-6=1,689.

Далее переходим к вычислению коэффициентов канонических уравнений по матричному выражению (1.6), связанному с перемножением матриц. При выполнении матричных операций следует помнить, что матрицы не подчиняются переместительному закону – их нельзя менять местами. Чтобы перемножить матрицу на матрицу нужно, для получения элемента результирующей матрицы, элементы строки первой матрицы умножить на элементы столбца второй матрицы и результаты сложить. Например:

        

         

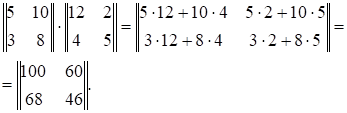
Реализуем матричное выражение L^T_y·F_y·T_y. Для этого перемножим транспонированную матрицу L^T_y на матрицу податливости F_y, получив промежуточную матрицу R₁. Транспонированная матрица L^T_y получается путем поворота столбцов матрицы L_y против часовой стрелки, при этом столбцы превращаются в строки транспонированной матрицы L^T_y.

                                   

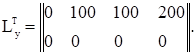
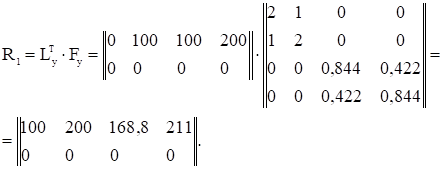
Уножим промежуточную матрицу R₁ на расширенную матрицу T_y. Матрица T_y получается путем приписывания с обратным знаком к матрице L_y матрицы L_Py:

                       

   

                                 

                                     =

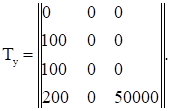
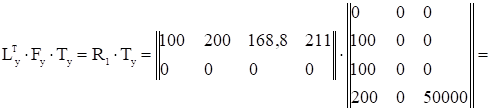
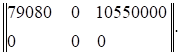
Выполним аналогичные матричные операции для второго слагаемого выражения (1.6), равного L^т_z·F_z·T_z. Обозначим R₂= L^т_z·F_z.

                        

                              

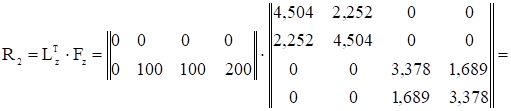
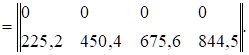
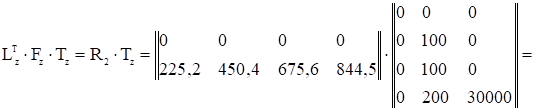
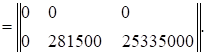
В соответствии с выражением (1.6) складываем полученные матрицы

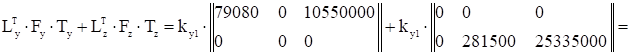
В полученной матрице два первых столбца образуют матрицу D, а третий столбец – присоединенный с обратным знаком вектор-столбец Δ грузовых коэффициентов.

                              

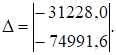
Матричное уравнение (1.2) метода сил для рассматриваемого примера имеет вид

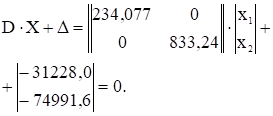
Так как канонические уравнения содержат только две неизвестных силы независимые друг от друга, то их проще найти  путем решения обычной системы алгебраических уравнений. В обычном виде приведенное матричное выражение имеет следующий вид:               (1.7)

Решая уравнения системы (1.7), получаем Х₁=133,409 кГ; Х₂=90,0 кГ.

В матричной форме вектор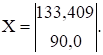

Зная вектор усилий (реакций), действующих взамен  отброшенных связей, по матричному выражению (1.4) находим ординаты расчетных эпюр внутренних усилий.

Вектор S_y , элементами которого являются ординаты расчетной эпюры изгибающих моментов, действующих в вертикальной плоскости, и вектор S_z, элементами которого являются ординаты расчетной эпюры изгибающих моментов, действующих в горизонтальной плоскости

  

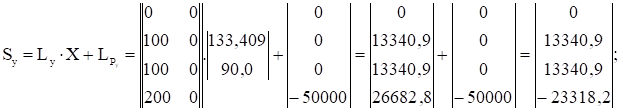
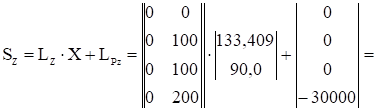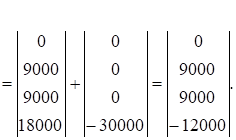
На рис. 1.1.,д показаны построенные по значениям векторов S_y и S_z расчетные эпюры изгибающих моментов, действующих в вертикальной и горизонтальной плоскостях.

Правильность выполненного расчета проверяется с помощью деформационной проверки, которая физически означает проверку отсутствия перемещений в направлении отброшенных связей. В матричном виде она представлена выражением (1.5). Применительно к рассматриваемому примеру расчета два последних слагаемых в выражении (1.5), связанные с кручением и растяжением-сжатием  равны нулю в силу указанных выше причин – имеющиеся связи не препятствуют кручению и растяжению-сжатию. В отношении указанных деформаций рассматриваемая система является статически определимой и напряжения при кручении и растяжении сжатии можно сразу определить по построенным грузовым эпюрам. Таким образом в рассматриваемом случае

                     

L^T_y·F_y·S_y + L^T_z·F_z·S_z = R₁·S_y + R₂·S_z = 0.         (1.8)

Так как деформации изгиба в вертикальной и горизонтальной плоскостях не зависят друг от друга, то каждое слагаемое в выражении (1.8) в виде произведения матриц должно быть равно нулю:

Если Вам понравилась эта лекция, то понравится и эта - Часть 56.

        

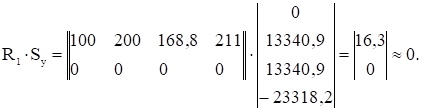
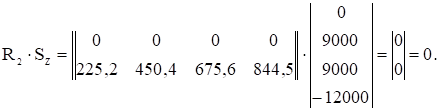
Ошибка при проведении деформационной проверки для первого слагаемого составила 0,00033%, а для второго – 0 %, что менее допускаемых 3%.

Ошибка определяется следующим образом: при перемножении строки матриц R₁ или R₂ на вектор-столбец Sy или Sz часть значений получается с знаком «+», а часть – с знаком «-». В идеале их сумма должна быть равна нулю. Если указанная сумма не равна нулю, то полученная разность принимается за Х%, а сумма положительных чисел (или отрицательных – меньшее из них) принимается за 100% и из этого соотношения определяется процент ошибки. Ошибка обычно связана с округлениями чисел при выполнении расчетов.

Пример расчета боковой рамы грузовой тележки типа ЦНИИ-Х3 с использованием матричной формы метода сил приведен в учебнике [1].

Как видно из численного примера, матричная форма метода сил представляет собой более формализованную, чем обычная форма, процедуру, что создает предпосылки ее использования при создании программ прочностного расчета вагонных конструкций на ЭВМ. В настоящее время приоритетное положение в сфере расчета напряженно-деформированного состояния вагонных конструкций занимает МКЭ. Вместе с тем рассмотренный выше метод находит свое применение при проведении экспертных оценок случаев, связанных с нарушением прочности вагонных конструкций в эксплуатации. В частности при использовании EXEL и матричной формы метода сил можно сравнительно быстро оценить напряженное состояние достаточно сложных пространственных стержневых конструкций.