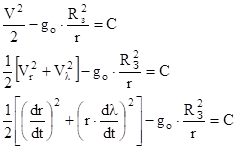Уравнение траектории пассивного участка .

Используем два полученных интеграла для вывода уравнений траектории пассивного участка .

Если точка движется в декартовой системе координат  ОXY  , то траектория имеет вид :

Y=f(x) , а в полярной системе координат :  r =f(λ)

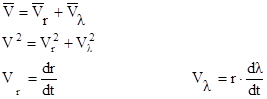
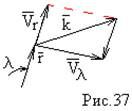
            Запишем уравнение энергии

Запишем момент количества движения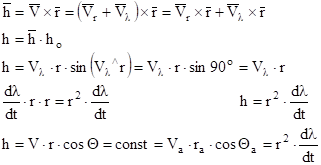

Имеется несколько неизвестных величин :  r , t , λ .

Чтобы получить уравнение траектории нужно избавиться от величины t .

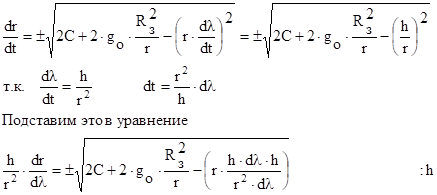
Рекомендуемые материалы

      - дифференциальное уравнение траектории пассивного участка .

Выбор знака “ ± “ зависит от выбора направления отсчета угла λ .

Если угол λ отсчитывается по часовой стрелке , то ставится знак “ - “ и наоборот . Так на рис.36  угол λ по часовой стрелке , следовательно при расчете нужно ставить знак “ – “ .

Чтобы решить это уравнение нужно ввести новую переменную :

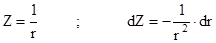
Тогда получим :

`

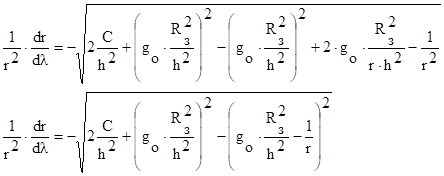
Подставим в это уравнение

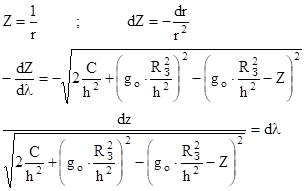
Уравнение с разделенными переменными

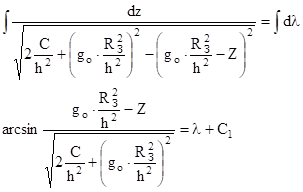
т.к. λ – это угол , то и С₁ тоже угол . Обозначим   φ=С₁ .

Избавимся от arcsin  и от дроби :

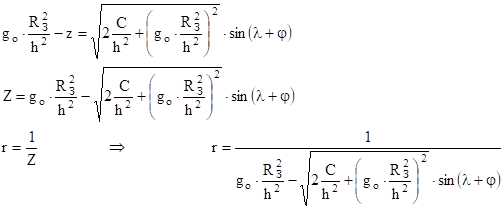
Ещё посмотрите лекцию "9.3 Общие представления о форматировании дисков" по этой теме.

Извлечем из под радикала выражение:  и поделим знаменатель на эту величину.

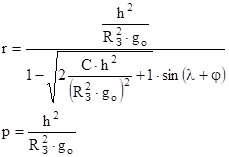
      - эксцентриситет траектории ;

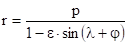
                Можно выбрать такое начальное положение плоскости n-n чтобы   

  - уравнение траектории полета ракеты на пассивном участке.

С точки зрения математики это уравнение которое образуется при пересечении конуса плоскостью (уравнение кривой).