Характеристики распределения случайных величин

3. Характеристики распределения случайных величин

3.1 Одномерная случайная величина

С. в. Х (одномерная) - величина, могущая принять различные вероятные значения х на некотором интервале (-¥£х£¥), т.е. х - возможное значение с.в. Х.

С. в. может быть дискретной и непрерывной. Вероятностные свойства с.в. Х характеризуются интегральной функцией распределения Р(x). Значение функции Р(x) равно вероятности обнаружить с.в. Х<х (или, что то же, на интервале ‑¥, х) т.е. Р(x)=Prob(X<x), где х - конкретная детерминированная величина.

Если с.в. Х может принимать лишь дискретные значения х₁, х₂,...х_n с вероятностями р₁, р₂,...р_n, то функция распределения представляет собой сумму вероятностей тех значений х_k, которые меньше х.

.                                                                 (12.3)

На рисунке Prob(X£x₃)=Р(х₃)=0,5, (т.е. Х=х₁ или Х=х₂ или Х=х₃). Prob(X=x₄)=0,6-0,5=0,1 (скачок равен вероятности появления значения х₄).

Функция распределения числа m наступления события в последовательности n независимых испытаний (согласно формуле (11.2)).

Биномиальный закон распределения:

Рекомендуемые материалы

        (13.3)

  .

Если с.в. Х непрерывна, то функция распределения имеет вид, показанный на рисунке.

Свойства функции распределения:

1)  Р(х) - неубывающая функция аргумента х

(т.е. при x₂>x₁ P(x₂)=Prob(X<x₂)>P(x₁)=Prob(X<x₁));

2)  При x=-¥ P(x)=0;

3)  При x=+¥ P(x)=1;

4)  Prob(x₁<X£x₂)=P(x₂)-P(x₁)                                                                                                         (14.3);

5)  Prob(X=x₁)=0. Вероятность обнаружить число, например 241.000...¥ равно 0. Однако, делая измерения, мы округляем значения, тем самым, увеличивая вероятность их появления. Например, округленное 241.0 содержит значения от 240.9500...¥ до 241.04999... ¥ и вероятность попадания числа в этот интервал не равна 0.

Распределение с.в. Х характеризуется также функцией плотности распределения с.в. Для дискретных значений с.в. функция плотности распределения может задаваться таблично. График функции р(х)=р_i при x=x_i изображен на рис.  .

Т.к. возможные значения x_i с.в. образуют полную группу несовместных событий (т.е. в каждом из n испытаниях с.в. обязательно примет одно из значений x_i с определенной вероятностью), то , где n - число испытаний.

Для непрерывной с.в. функция плотности распределения имеет вид, показанный на рисунке.

Если функция распределения с.в. Р(х) - непрерывна, то                                (15.3)

или . По непрерывной кривой плотности распределения, в отличие от дискретной, вероятность обнаружить точное число х₂ равна нулю. При помощи функции р(х) вероятность обнаружить с.в. Х в бесконечно малом интервале x<X<x+dx равна Prob(x<X<x+dx)=p(x)dx (площадь прямоугольника, dx®0). То же в конечном интервале x₁<X<x₂:

                                                             (16.3)

(Геометрически это заштрихованная площадь под кривой плотности распределения).

Из (15) следует, что                                                                             (17.3),

поэтому функцию распределения называют еще интегральной функцией распределения.

Свойства функции плотности распределения:

1)  Плотность распределения вероятностей - неотрицательная функция р(х)³0.

2)                                                                                                                                    (18.3),

что эквивалентно Р(¥)=1.

3) Размерность р(х) обратная размерности с.в., а Р(х) - безразмерна.

4) Числовые характеристики распределения

Математическое ожидание с.в. Х :

 - дискретной

                                                                      (19.3)

при этом               (М(x) - случайна при n¹¥).

 - непрерывной

                                                                        (20.3).

Математическое ожидание  - достоверная величина, т.к. вероятность того, что при n=¥ испытаниях мы получим среднее арифметическое М(X)= равна 1.

М(с)=с,   М(сx) = сМ(x), где с – неслучайное число.

Для независимых с.в. Х₁ и Х₂

М(x₁+x₂)=М(x₁)+М(x₂), М(x₁x₂)=М(x₁)М(x₂), М(x²)=[М(x)]²+D(x).

К математическому ожиданию стремится среднее арифметическое наблюдаемых значений с.в. при количестве испытаний n®¥. Геометрически м.о. – это абсцисса ц. т. площади под кривой плотности распределения. Размерность м.о. совпадает с размерностью с.в.

Дисперсия с.в. Х - м.о. квадрата отклонения с.в. Х от ее м.о. (центра распределения):

D(x)=M[x-M(x)]²=M(x²)-M²(x),

т.к. M[x-M(x)]²=M[x²-2xM(x)+M²(x)]=M(x²)-2M²(x)+M²(x),

M[2xM(x)]=2M²(x) и M[M(x)]=M(x).

Дисперсия дискретной с.в. Х

                                                               (21.3)

случайна при n¹¥.

Дисперсия непрерывной с.в. Х:

                                         (22.3),

(дисперсия непрерывной с.в. - достоверна).

 - математическое ожидание.

Дисперсия характеризует разброс с.в. вокруг ее среднего значения (математического ожидания).

D(c)=0,

D(cx)=c²D(x),

D(c+x)=D(x).

Доказательство.

 D(cx)=M[cx-M(cx)]²=M[c²x²-2cxM(cx)+M²(cx)]=

c²M(x²)-M[2c²xM(x)]+M[c²M²(x)]=

c²M(x²)-2c²M²(x)+c²M²(x)=

c²[M(x²)-M²(x)]=c²D(x). D(c+x)=

M[c+x-M(c+x)]²=M[c+x-c-M(x)]²=M[x-M(x)]²=D(x).

Для независимых с.в. Х₁ и Х₂  D(x₁±x₂)=D(x₁)+D(x₂).

Геометрически дисперсия – это центральный момент инерции площади под кривой плотности распределения. Размерность дисперсии - квадрат размерности с.в.

Среднеквадратическое отклонение (стандарт): .

Асимметрия непрерывной с.в. Х:

                                                           (23.3).

Если с.в. Х распределена симметрично относительно своего м.о., то А(х)=0.

Коэффициент изменчивости (вариации) с.в. Х - отношение стандарта к м.о.:

                                                                   (24.3).

3.2 Случайная векторная величина двух измерений

На практике решаются задачи, в которых результат опыта описывается не одной с.в., а двумя или более с.в., образующими систему. При этом свойства системы нескольких с.в. могут включать и взаимные связи (зависимости) между ними.

Если с.в. X и Y принимают дискретные значения x_i, y_j и каждой паре значений (x_i, y_j) соответствует определенная вероятность p_ij, то можно составить таблицу распределения вероятностей дискретной двумерной с.в.

Очевидно .

Значение функции Р(x,y) равно вероятности обнаружить с.в. Х<х и с.в. Y<y, т.е.

P(x,y)=Prob(X<x,Y<y).

Свойства функции распределения Р(x,y):

1) Р(х,y) - неубывающая функция своих аргументов,

т.е. при х₂>x₁ P(x₂,y)>P(x₁,y) или при y₂>y₁ P(x,y₂)>P(x,y₁);

2) P(x,-¥)=P(-¥,y)=P(-¥,-¥)=0;

3) P(x,+¥)=P(x), P(+¥,y)=P(y) - если один из аргументов равен +¥, то функция распределения Р(х,y) превращается в функцию распределения другой с.в.;

4) P(+¥,+¥)=1.

Плотность распределения системы двух с.в. (вторая смешанная производная P(x,y) по  и затем по ).

                                                  (25.3)º(15.3)

или в общем виде

, .

Геометрически p(x,y) можно представить поверхностью (поверхность распределения - по ОХ и OY откладываются значения с.в. X и Y, по Z - вероятность их появления, см. рис.  ).

Из (25) следует

                                                  (26.3)º(17.3).

Вероятность обнаружить двумерную с.в. (X,Y) в области D:

Prob((X,Y)ÌD)=                                        (27.3)=(16.3).

Вероятность обнаружить точку М с координатами х₁, х₂,...х_n в n-мерном объеме V:

Prob(MÌV)=                                (27¢.3)

Далее, аналогично (18)

                                                              (28.3),

т.е. геометрически объем под поверхностью распределения равен 1.

В общем виде имеем n-кратный интеграл

                                            (28¢.3).

Если известен закон распределения системы двух случайных величин p(x,y), то можно определить законы распределения отдельных величин, входящих в систему:

                                                                      (29.3).

То же, в общем виде:

                              (29¢.3).

Но для того, чтобы по заданным законам распределения отдельных с.в., входящих в систему, определить законы распределения системы с.в., надо знать зависимость между величинами, входящими в систему.

Условный закон распределения с.в. Х, входящей в систему (X,Y) - закон ее распределения, вычисленный при условии, что другая с.в. Y приняла определенное значение. Условный закон распределения можно задавать функцией P(x/y) и плотностью p(x/y) распределения.

Геометрически функция плотности распределения p(x/y) представляет собой сечение поверхности распределения при y=const. Сечения поверхности распределения плоскостями x=const и y=const дают соответственно условные плотности распределения p(y/x) величины Y при определенных значениях x и условные плотности распределения p(x/y) величины X при определенных значениях y. Если X и Y - зависимые с.в., то кривые плотности распределения p(y/x) изменяются при изменении x, а кривые плотности распределения p(x/y) изменяются при изменении y. М.о. этих кривых при таких изменениях образуют линии регрессии 1 и 2. В случае независимости X и Y линии регрессии представляют собой прямые  и , параллельные осям координат. При наличии функциональной связи (а не стохастической) между X и Y обе линии регрессии сливаются в одну - y=y(x), при этом поверхность плотности распределения может быть заменена кривой плотности распределения X или Y вдоль линии y=y(x).

С учетом вышесказанного плотность распределения системы двух с.в. равна плотности распределения одной из них, умноженной на условную плотность распределения другой величины, вычисленную при условии, что первая величина приняла заданное значение:

p(x,y)=p(x)p(y/x)                                                         (30.3)=(7.2)

или в общем случае

p(x₁,x₂,...,x_n)=p(x₁,x₂,...,x_i/x_i+1,x_i+2,...,x_n)p(x_i+1,x_i+2,...,x_n)                               (30¢.3).

Для независимых с.в. p(x,y)=p(x)p(y)  (31)=(3) - плотность распределения системы независимых с.в. равна произведению плотностей распределения отдельных величин, входящих в систему.

3.3 Числовые характеристики распределения системы двух случайных величин

1)  М.о.                                   ,                            (32.3)

или в общем виде                                                    (32¢.3).

Геометрически точка  является проекцией на плоскость XOY центра тяжести объема, ограниченного поверхностью распределения p(x,y).

2)  Дисперсия:             (33.3).

3)  Корреляционный момент с.в. X и Y:                               (34.3).

Корреляционный момент характеризует стохастическую зависимость между с.в. а также рассеивание. Корреляционный момент - м.о. произведения отклонений двух с.в. от их мат. ожиданий , при .

Корреляционный момент - достоверная величина.

Если зависимости между X и Y нет, то K_xy=0, но из того, что K_xy=0 не следует независимость X и Y.

С.в. могут быть:

1) Независимы, т.е. не коррелированы K_xy=0;

2) Зависимы и коррелированы K_xy¹0;

3) Зависимы и не коррелированы K_xy=0 (если поверхность плотности распределения симметрична относительно осей координат OX и OY, т.е. M(X)=M(Y)=0).

4)  Коэффициент корреляции:      ,                                                                             (35.3)

где  - стандарт.

-1£ r_xy £1 - характеризует степень тесноты линейной зависимости между с.в. r_xy=1 при Y=aX+b (линейная функциональная стохастическая связь).

При нелинейной функциональной связи r_xy<1. При отсутствии стохастической связи r_xy=0 - необходимое, но недостаточное условие независимости X и Y.

Систему n с.в. можно охарактеризовать n м.о. , n дисперсиями  и n(n-1) корреляционными моментами K_XiYj  с i ¹ j (при этом K_XiYj=K_XjYi).

3.4 Функции случайных величин

Функция с.в. будет также случайной величиной Y=j(X). Ее распределение соответствует распределению аргумента, но с измененной шкалой абсцисс. P(y)=Prob(Y<y)=Prob(j(X)<y).

                                               (36.3)=(17.3),

где  y(y) - функция обратная j(х) (замена подинтегрального выражения x=y(y), dx=y¢(y)dy).

Если Y=j(X), где j(X) - монотонная функция своего аргумента, то распределение Y определяется тем, что вероятность нахождения y в пределах y₁<Y<y₂ равна вероятности неравенства х₁<X<x₂,

где y₁=j(x₁) и y₂=j(x₂).

М.о. и дисперсия с.в. Y:

           (37.3)=(20.3) и (22.3).

Доказательство (37.3):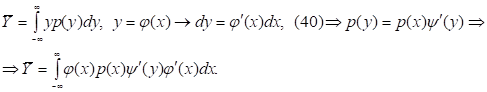

Для линейной функции Y=aX+b из (37.3) и (18.3) следует

 и D(Y)=a²D(X)             (38.3).

Доказательство (38): .

Для функции Z=j(X,Y) двух случайных аргументов м.о. и дисперсия                   (39.3).

Если Z=j(X,Y)=X+Y и X и Y - независимы, то м.о. и дисперсия суммы независимых с.в. величин D(Z)=D(X)+D(Y).

Плотность распределения непрерывной с.в. Y, связанной монотонной функциональной зависимостью Y=j(X) с непрерывной с.в. Х:

 или                                        (40.3),

где x=y(y) - функция обратная y=j(x).

Для линейной функции y=ax+b из (40) следует

p(y)=(1/a)p(x)                                                                    (40¢.3).

Если Y=j(X/R) и p(x/r) - условная плотность вероятности с.в. Х, входящей в систему (X,R), то условная плотность вероятности с.в. Y - ,

где y(y/r) - функция обратная Y=j(X/R), а безусловная плотность вероятности с.в. Y:

,

где p(r) - плотность вероятности с.в. R.

Если имеются функции с.в. U=U(X,Y) и V=V(X,Y), то, зная совместную плотность распределения p(x,y), совместная плотность распределения U и V:

                             (41.3)

(в скобках - Якобиан ).

Матожидания:                                       (42.3),

дисперсия           ,

корреляционный момент            .

В случае линейного преобразования U=a₁X+b₁Y+c₁ и V=a₂X+b₂Y+c₂  по (41.3) и (42.3) имеем:

                                                          (43.3),

 и                                          (44.3).

Дисперсия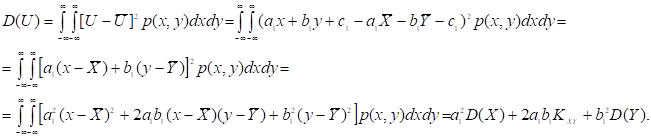

Доказательство (44)

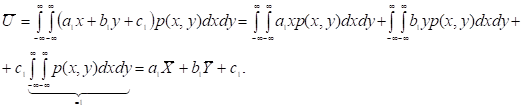
Запишем еще раз дисперсии и корреляционные моменты:

,          ,  (доказать самостоятельно).

Зная плотность распределения p(U,V), где U=U(X,Y) и V=V(X,Y), можно определить плотность распределения p(U) или p(V): .

Пример (стр.23 [7]). Стержень нагружен изгибающим моментом M_b и крутящим моментом M_t, и есть их совместная плотность вероятности p_q(M_b,M_t). Кроме того, моменты M_b и M_t стохастически независимы и подчиняются центрированному нормальному распределению:

,

где s_b и s_t – стандарты M_b и M_t.

Опасное состояние стержня достигается при превышении некоторой функцией этих моментов предельного значения M_r>M_r,lim, зависящего от свойств материала и геометрии сечения стержня. Например, для стержня круглого сечения из пластического материала эта функция может быть взята в виде , где M_r – приведенный момент, определенный в соответствии с критерием текучести, основанном на наибольших касательных напряжениях.

Касательное напряжение от крутящего момента , где I_r - полярный момент круглого сечения, y – радиус окружности, содержащей рассматриваемую точку, t = t_max при y=r (r – радиус стержня). Нормальное напряжение от изгибающего момента . Для расчета надежности стержня необходимо знать плотность вероятности p_u(M_r) приведенного момента M_r.

Перейдем к полярным координатам, положив , где 0£q£2p. Согласно (41.3) совместная плотность распределения с. в. M_r и q:

Люди также интересуются этой лекцией: 6 Криминалистическая видеозапись.

.

Используя  и замечая, что якобиан преобразования ,

найдем

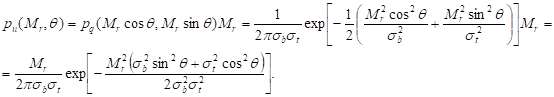
Плотность распределения вероятности p_u(M_r) определяется интегрированием полученной формулы по углу q: . Используя формулу анализа , где  - функция Бесселя мнимого аргумента нулевого порядка, получим окончательно             .

Если дисперсии моментов M_b и M_t одинаковы, т.е. s_b=s_t=s, то I₀(0)=1 и . При этом приведенный момент подчиняется распределению Рэлея.