Лекция 3.

3. Определение напряжений в массивах грунтов.

Напряжения в массивах грунтов, служащих основанием, средой или материалом для сооружения, возникают под воздействием внешних нагрузок и собственного веса грунта.

Основные задачи расчета напряжений:

- распределение напряжений по подошве фундаментов и сооружений, а также по поверхности взаимодействия конструкций с массивами грунта, часто называемых контактными напряжениями;

- распределение напряжений в массиве грунта от действия местной нагрузки, соответствующей контактным напряжениям;

- распределение напряжений в массиве грунта от действия собственного веса, часто называемых природным давлением.

3.1. Определение контактных напряжений по подошве сооружения.

При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения.

Характер распределения контактных напряжений зависит от жесткости, формы и размеров фундамента или сооружения и от жесткости (податливости) грунтов основания.

3.1.1. Классификация фундаментов и сооружений по жесткости.

Различают три случая, отражающие способность сооружения и основания к совместной деформации:

Рекомендуемые материалы

- абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания и при определении контактных напряжений сооружение можно рассматривать как недеформируемое;

- абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания;

- сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений.

Критерием оценки жесткости сооружения может служить показатель гибкости по М. И. Горбунову-Посадову

,                                                 (3.1)

где  и  - модули деформации грунта основания и материала конструкции; и  – длина и толщина конструкции.

3.1.2. Модель местных упругих деформаций и упругого полупространства    

При определении контактных напряжений важную роль играет выбор расчетной модели основания и метода решения контактной задачи. Наибольшее распространение в инженерной практике получили следующие модели основания:

- модель упругих деформаций;

- модель упругого полупространства.

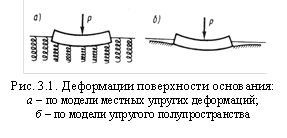Модель местных упругих деформаций.

Согласно этой модели, реактивное напряжение в каждой точке поверхности контакта прямо пропорционально осадке поверхности основания в той же точке, а осадки поверхности основания за пределами габаритов фундамента отсутствуют   (рис. 3.1.а.):

,                                                   (3.2)

где  – коэффициент пропорциональности¸ часто называемый коэффициентом постели, Па/м.

Модель упругого полупространства.

В этом случае поверхность грунта оседает как в пределах площади загрузки, так и за её пределами, причём кривизна прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании (рис. 3.1.б.):

,                                        (3.3)

где  - коэффициент жесткости основания,  – координата точки поверхности, в которой определяется осадка;  - координата точки приложения силы ; – постоянная интегрирования.

3.1.3. Влияние жесткости фундаментов на распределение контактных напряжений. 

Теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям. Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуется более пологой кривой и у края фундамента достигает значений, соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 3.2.а.)

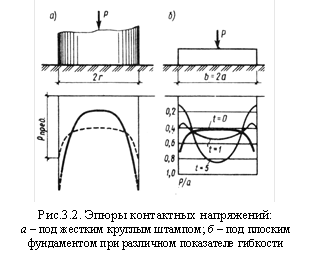Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 3.2.б. приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5.

3.2. Распределение напряжений в грунтовых основаниях от собственного веса грунта.

Вертикальные напряжения от собственного веса грунта на глубине z от поверхности определяются формулой:

,                                                       (3.4)

Бесплатная лекция: "4 Аккумулирование ливневого паводка" также доступна.

а эпюра природных напряжений будет иметь вид треугольника (рис. 3.3.а)

При неоднородном напластовании с горизонтальным залеганием слоев эта эпюра будет уже ограничиваться ломаной линией Оабв, где наклон каждого отрезка в пределах мощности слояопределяется значением удельного веса грунта этого слоя (рис. 3.3.б).

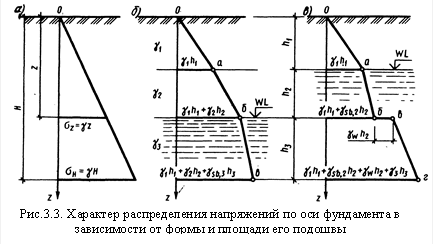
Неоднородность напластования может вызываться не только наличием слоев с разными характеристиками, но и наличием в пределах толщи грунта уровня подземных вод (WL на рис. 3.3.в). В этом случае следует учесть уменьшение удельного веса грунта за счет взвешивающего действия воды на минеральные частицы:

,                                             (3.5)

где  - удельный вес грунта во взвешенном состоянии;  - удельный вес частиц грунта;  - удельный вес воды, принимаемый равным 10 кН/м³;  – коэффициент пористости грунта.